Leaderboard

The more physics one studies the more interconnected one realizes different theories get +1

First of all, as @Mordred pointed out, this is from Quanta Magazine, which is not a peer-reviewed scientific publication. Second of all, if that were true, it doesn't mean it validates the numerology of paper under discussion. Third of all, you chose to ignore morsels of language that are very relevant: [...] may be [...] [...] hints that [...] [...] If true, it would be [...] [...] It's possible we're seeing [...] And, above all, (from provided source; my emphasis.) All of that you interpret as "actually, vacuum dilutes [...]" I'm kinda old. I've seen many, many 'earth-shattering' discoveries come and go: Antigravity, cold fusion, superluminal neutrinos, and what not.

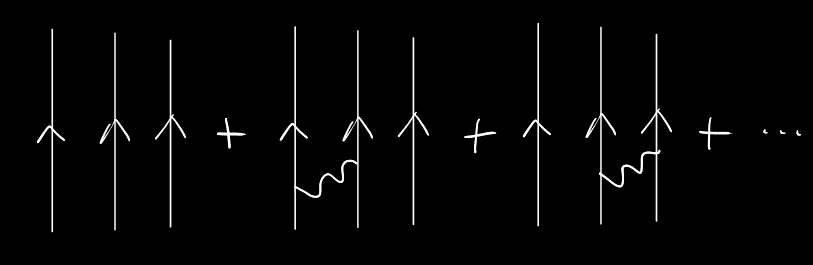
@Albert2024, @JosephDavid, and the other guy, Let's hammer it home again. At some point somebody among you will understand (one can only hope). No vacuum in QFT has external legs. The vacuum in QFT is made up of things that look like, This means, in a manner of speaking, that the amplitudes (infinitely many of them) go from nothing to nothing. The vacuum state gives zero as expected value for the number operator of each and every particle. That, people, is what we call a vacuum. And thereby the name. A vacuum ultimately has nothing in it, except for amplitudes of something appearing there, and swiftly disappearing, according to quantum rules (HUP). Vacuum = nothing. Doh! OTOH, In the diagramatics of QFT, the "vacuum" this "paper" seems to be talking about would look something like this, That is, it has external legs (real particles that go from \(t=-\infty\) to \(t=+\infty\). In the picture I've represented a triplet of SU(3). It could be an octet, or whatever. Maybe not even an irreducible rep. of SU(3). What have you. It would have ramifications displaying vacuum polarisation, and so on. The point is: This is no vacuum. These "atoms" are there, and they keep there. Do you understand? Do you? Really? Do you, at long last, understand? Precision tests of the standard model would have detected this background (rather than vacuum) long ago, because other particles would scatter off these "atoms" copiously (among other things they would have to be 1043 times more abundant than nucleons and electrons, and 1033 times more abundant than photons. So, presumably, your beloved paper has been turned down experimentally ages ago. Remember this comment, which you also chose to ignore?: Maybe it's another completely different SU(3) gauge group, with its own coupling constant and all. You tell me. I don't have to read the article, as per SFN rules. If my arguments are wrong or misplaced, then answer them, instead of cajoling each other with idle pleasantries and even idler reputation points, plus meaningless punishing -rep points, as @Mordred pointed out. And that will be all, unless you finally come up with real counter-arguments from physics. Bye.

For while now, I've been slowly trying to learn Finnish, since it was the natural tongue of all my grandparents. However this isn't going to be strictly about that but abut learning languages in general. They often start by teaching you a few simple phrases, that may come in useful, (hello, my name is... etc.) One of those phrases is often along the lines of "Do you speak English(or whatever language you normally speak)? For example, in Finnish, this would be "Puhetko* englanitia?" After some thought, I realized that there is no real reason you need to know how to say this. If you were in Finland and wanted to ask someone if they spoke English, you could just ask in English. If they do, they will understand you, and answer in English, and if they don't, they'll say something like "Ei"( no), or "en ymmärrä"( I don't understand), or give you some other indication that they don't. Either way, you've got your answer. Now, I can see where it would appear more polite to ask in Finnish( or in whatever the language is where you are), but in a purely logical sense. it is not strictly necessary. And of course, the one thing you definitely shouldn't do if you get the second response is to ask the question again, but LOUDER.... AND....SLOWER. *or "puhutteko" if you being formal or addressing more than one person.

I don't know who will win. I don't thinks anyone does. But here's a hint about who I would like to win.

Shouldn't the sum of all spins of the fermions in my body sometimes add to n + 1/2 so I am a fermion as a whole? Then by turning around 2 times I should look in the opposite direction. I try several times per day, but it never happened. Physics is wrong!

That's not the way to look at....you should in a manner,the volume coming out of a blackhole...remember in holography volume is an illusion...

What am learning from you is that to get a solution of anything it's so difficult and requires complexity of mathematics beyond comprehension....what am asking myself is that,if there was such an attitude 120 years ago I doubt if the theories such as GR could have been accepted were it not for experimental support they got...almost majority of solutions are approximation. Am trying to think from a holographic perspective if there is an experiment that can be designed factoring in Bose Einstein condensate to look at 1/100^123 validity.

You are giving an answer and yet you can't see it from the explanations...soo weird.

Strong-weak duality.....strong force-gravitation... arbitrary chosen not because it gives desired answer but it's because it's the right parameter to choose and it gives the correct answer..otherwise from the duality which other parameter can you choose?

There is that fancy trend nowadays of trying to discredit any kind of achievement....where do you think breakthrough fundamental discoveries should come from?...paraphrasing people's ideas to suit you own discredit and proof them wrong,while not trying to answer why it is wrong..shows how rigid someone tend to be.

Good point. I was thinking of using reflections too, until I remembered fermions. I don't think children would care too much about fermions tho... I agree. Any other choice would give you problems with the distributive property and/or other equally fundamental properties though. After all, there must be a reason why we've been choosing that option and no other one has resulted in an interesting algebraic framing.

Well you have been disappointingly combative towards replies in this thread. I thought you wanted to discuss this excellent subject and I welcome the input and ideas from several others. Out of interest here is what Richard Courant the famous Mathematician and mathematical educator has to say on the subject: Note carefully he claims that it is impossible to proove that (-1) x (-1) = +1. I has to be defined that way.

Sometimes am having problem accessing the thread. When I joined this forum I had a theory developed with sheer logical reasoning and minimum already established scientific facts like charges of a quark,and published a book about it in a most basic layman language,my background is not physics oriented but I believed we need a basic theory that someone need to go back to and make references from it's principles....and if this theory is the actual basic theory then answers should get along with it....that's a long story. My perspective come from the fact that if I compare what I have and assuming the calculations of the author is correct and putting the fact that he is comparing superconductor effects with dark matter/dark energy....to reconcile both concepts then holographic principle emerges as a natural solution...this is also bringing confusion to my understanding.. the reason then why the number of SU(3) units it's not getting a long with the number of photons and protons in the universe is the way this holograph is being projected,the projection 'might' being interfered with by quantum noise....the information is encoded on the surface of of SU(3) structure (remember this)... quantum noise is coming from quantum soup.... universe expansion reduces temperature hence reducing quantum noise overtime(refining the projection).....meaning the solution the author is introducing is a constancy of proportionality-the rate at which this refining is taking place i.e how the classical universe governed by GR is emerging from quantum world governed by QFT.....hope that's not too much.

I will tend to differ with your conclusion,the scale was not chosen randomly their is a reason behind it.what the author is doing is a continuation of arguments present in the video you posted above. I think if there was a specific directions such a solution is supposed to come from it should have been arrived at longtime ago. By the way,thanks for the video,it's a good learning material.

Your POV always seems like a parody to me, like you're just trolling to get people to comment on ridiculous statements. "I hate scientists who make weapons, but appreciate the ones who protect Americans!" Your reality has lots of noise and very, very little signal.

It's creating a correspondence in SU(3) concept and cosmological constant problem....I think beyond that no need to import SU (3) mathematics. The author seem to have other papers that are heavy mathematically,after a quick online search, therefore,he is not limited in that perspective. For me I also have my own thinking (concepts) that's makes/helps me leapfrog the current arguments and see in much deeper angle...the holographic perspective...and I can assure you it's much amazing 🤩...it's weird how scientific concepts from different backgrounds link tonger... Einstein saying 'we can't solve problems with the same thinking we used to create them'

..and what Joigus has stated excess of proton in the order of 10^43...after thinking and from what am having,comparing that with how the author is solving cosmological constant problem...we may be dealing with holographic principle,any error arising in transmission may be due to quantum noise,to me this is amazing since I never thought of it (holographic principle) to be possible,I took it to be fiction, in this case I see it can be real...this is amazing 🤩.

Is there anything wrong with the formulas employed by the author? According to my views the math appears to be straight forward...if the formulas are correct it mean the math is okay, however, the arguments about derivation of N ( SU 3 atoms) should be controversial.

Your dreams reflect your conscious brain trying to make sense of unconscious activity and striving to apply a narrative to that makes sense in context of the items you’re thinking about while awake. You’re obviously thinking of physics concepts and sci interfere that’s the frame under which your mind explains your dreams to yourself. Nothing to do with quantum theory tho

This “my teacher hates me” take is a dime-a-dozen, so I’m not surprised to see it. But the truth is you broke the rules - the specifics were pointed out to you - and that’s why it was locked. You didn’t post “hard facts,” you spammed us with videos, and you escalated the rhetoric. And I don’t know what-all this has to do with academia; did you think you had wandered onto a college campus? We’re willing to host reasoned discussion, and the rules are set up to facilitate that. Follow the rules, and you can present your argument. If you don’t follow the rules, threads get locked.

"Little children" in my question are school kids which are taught this rule - 3rd grade? As I don't remember any explanation given then to me, I think that there was not one. Like above. Just a rule. I wonder, is it still this way? Everywhere? "Hand waving" explanations like in the book posted by @studiot and the odd-even metaphor recalled by @MigL help perhaps to "get" the rule. How about a "Guess the Rule" game? Let them come up with a possible rule and find that other suggestions don't work?

What I do remember is the story of the teacher saying that, while two negatives make a positive, two positives still make a positive. To which a voice at the back of the class remarked: "Yeah. Right".

Sure but I would prefer to take the time to find half decent literature examples in this case. A large part of it is different methodologies to handle the nonrenormalization of the findings of the Nambu-Jona-Lasinio model mentioned here. This is a huge part of the reason for all the SU(3) lattice gauge articles you guys are finding. This all is also part of BCS theory mentioned in below link https://en.m.wikipedia.org/wiki/Nambu–Jona-Lasinio_model But in this case I'm only loosely familiar with some of the research as it's not one of my specialty areas in so far over the years I've read numerous articles on the topic and some of the research but don't particularly follow it closely or rather not as much as I do in early universe processes as I'm a Cosmologist with formal training in Cosmology and particle physics. One detail to recognize is that a gauge theory such as SU(3) isn't necessarily identical in every treatment that's one of the things recognize when it comes to gauge theories. A good example is the distinctions between QM and QFT they both use SU(3) but the operators themselves in each case are different. So it's essential to look specifically how any given theory applies a given gauge group.

An article published yesterday by The New Republic (TNR) discusses at some length the malign influence of so called ‘polls’ released by right leaning US firms in the last few weeks, which in a number of cases appear to be openly partisan attempts to shift the aggregate polls in favour of Trump, and to create a false illusion of momentum trending in favour of MAGA https://newrepublic.com/article/187425/gop-polls-rigging-averages-trump What is happening is that the psephological marketplace is being flooded with new polls from right-wing fly-by-night operators, and this data is then being included into national polling averages by such aggregators as FiveThirtyEight and The New York Times - among others. The latter adamantly deny that GOP polls are seriously harming their averages and forecasts - but a better question would be - Why is this garbage being included by aggregators in the first place ? The aggregators say that they apply negative weightings to polls which are thought to be systematically biased to ensure they have less influence than high-quality polls with better standards of empirical accuracy and more methodological transparency. Critics are sceptical about this - and with reason.They point out that while many of the distortions introduced into the averages by these skewed MAGA leaning polls may be statistically insignificant - e.g. a ‘lead’ of 0.4% - they are being actively exploited for psychological propaganda effect by social media entities such as X/Twitter who will claim that Trump is “Winning the state”, and then even more irresponsibly assign electoral college votes based on such narrow leads to ramp up partisan claims that ’Trump is now winning’ - not just even leading, but winning the election - when the underlying data says nothing of the sort. Earlier today I read a report on Sky News whose headline uncritically claimed that “Trump is now the bookies favourite” https://news.sky.com/story/us-election-donald-trump-kamala-harris-democrat-republican-polls-skynews-live-latest-13209921 The reality (as previously noted) is that these claims derive entirely from online betting markets like Betfair and Polymarket which are being heavily manipulated by conservative MAGA investors who are sinking up to $14 million dollars a time into these forums - precisely to generate headlines of this sort.

ChatGPT, is that you?

I won't accept such cookies normally, but I pasted the link in an incognito window and it let me in without challenge. It seems to be a Newtonian calculator and yields 1.18c if I put in 10k hours at 1G Really, there are very good calculators for relativistic space travel. One of the best: https://gregsspacecalculations.blogspot.com/p/blog-page.html That one presumes fixed proper acceleration, not coordinate acceleration like a Newtonian calculator would use.

It seems to be an either cookies, else subscribe wall. They never guess right what adds I'm interested in, so I always take them with the default settings.

That's coordinate acceleration, and 1G of that for almost a year would kill poor Joanne, and it could not continue at all for a full year. I do realize the OP did not specify explicitly, but 'comfortable' was used, so my figure is based on a comfortable 1G proper acceleration, and that takes almost 2.7 years (ship time) to get to that speed and around 6.8 years Earth time. Fixed proper acceleration can in principle be kept up indefinitely. Oh, and your link is behind a paywall, or at least a subscribe wall. I could not view it.

1g acceleration gets you to 0.99c in a little less than a year (earth frame) https://rechneronline.de/g-acceleration/

Switch that around the the coupling strength gets stronger at low temperatures due to asymptotic freedom weakest as temp increases. See second graph coupling strength on Y axis conversion from GeV to Kelvin 11606 Kelvin per eV for x axis The article has zero mathematics for SU(3) so it's claims on that regard That really amounts to trying to build a workable model for the Author as none of those mathematics are inclusive.

Oh, i see.. hmmm, well, in that case i'm gonna have to re-examine it a bit more, thanks for the heads up =/

I’m afraid that makes little sense…spacetime (however many dimensions you give it) is either geodesically incomplete, or it isn’t. This is not an observer-dependent notion. Extra macroscopic dimensions would be easily noticeable in the effects their existence has on the laws of physics. For example, in a (4+1)D universe, radiation fields would fall off with distance according to an inverse cube law, rather than an inverse square law. This is evidently not what we see in the real world. This isn’t what happens in GR, so what you are attempting to formulate is a modified law of gravity. That is good and well, but the major problem is of course that such a modified theory must also correctly model all other gravitational scenarios, not just gravitational collapse. This is where all known modified gravity theories (and there are many at this point) ultimately fail - some do very well in specific scenarios, but fail miserably in other situations. Right now only GR provides the best fit for the largest set of available data. This is actually a pop-sci misconception - collapse processes don’t lead to “infinitely dense point”. But that aside, when it comes to avoiding singularities, this is really not so hard to do; for example, simply allowing torsion on your spacetime does the trick (the resulting theory is called Einstein-Cartan gravity). The trouble with all those modifications is that they have other consequences too; for example, the above model leads to extra terms in the Dirac equation, making it non-linear, and there’s currently no observational evidence of any deviations from the standard form of the equation. Thus - proposing models that fix specific issues is quite easy, but making these models also agree with all other available data, that’s hard.

I'm afraid that you cannot get to that speed (relative to Earth) in only half the distance to your destination (at least not at 1G). Perhaps a target further away like Tau Ceti, which is almost exactly how far you'd get if you got to .99c and immediately started slowing. You'd be back home in 27 years 2.3 months. To Alpha Centauri and back you'd be gone only 12 Earth years, but would only reach 0.95c Tell Joanne to skip most of the luggage and have laundry facilities onboard.

Here are some equations that may help Where: t =Earth time T= ship time d= distance v = velocity a= acceleration For brevity: ch = hyperbolic cosine sh = hyperbolic sine th = hyperbolic tangent t=(c/a) sh(aT/c) = sqrt[(d/c)2 + 2d/a d=(c2/a) [ch(aT/c)-1] = (c2/a) (sqrt[1+(at/c)2]-1) v= c th(aT/c) = at/sqrt[1+(at/c)2] T= (c/a) sh-1(at/c) = (c/a) ch-1[ad/c2 +1]

While the parts with constant relative speed require just algebra, the acceleration and deceleration are more involved. E.g.,

It's a half truth. Inflation from quantitative easing and "printing money" could lead to inflationary effects. It's just not the root cause of the inflation most people are bitching and moaning about right now. That was due to supply chain shocks globally at the same time that families received rapid unexpected injections of cash to prevent collapse of the system. This would potentially help with inflation since it would remove liquidity from the system (i.e. poor people stop spending money and the reduction in spending would lead to lowering of costs vendors and manufacturers charge), but a far superior weapon is increasing interest rates since it's not regressive and has the benefit of impacting everyone all at once.

The author is dealing with spacetime its self...the layout of the universe it's self..the basic, fundamental vacuum....on page 16 he talks about sentience and self replication....I hope you now get the idea...that's why am talking of a concept from this forum a year ago, specifically speculation section?????????. I don't mean quantum noise. No further queries.

.....mmmm....the idea has been in this forum for almost a year before this paper was published but in a different perspective...it seems the concept is diffusing to other people or just a coincidence,I don't know...it's the concept that matters...I understand the defender...you won't agree with them..I think the author is getting math that happens to solve the cosmological constant issue...I don't know if he has further insight beyond that....I also would want to know if the author has ever visited this forum to get inspiration... nowadays information flows at lightening speed.the author is using a concept to solve an already existing problem.

How I felt like reacting when I found out most of my new coworkers are Trump supporters... Because yes, they are Orcs.

Actually, he is. Here is how: Firstly, he is i.e., he is calculating the ratio, (universe volume)/(SU(3) effective volume). Then, he is dividing the energy density by this ratio, i.e., he is calculating, (energy density)/(universe volume)*(SU(3) effective volume). Or, equivalently, (energy density)*(SU(3) effective volume)/(universe volume). So, he is in fact

It is is numerology when it doesn't apply any boundary conditions without the relevant proof of how those boundary conditions are being applied. Particularly since that value exceeds to estimated total particle number count of 10^90 particles for the entirety of the SM model of particles. That estimation is based of the number density of photons using the Bose-Einstein statistics at 10^{-43} seconds so the 10^{123} value would entail conservation of energy mass violation. Lol keep it coming love the childishness ( little forewarning though one can lose their ability to use the reputation system.) Our forum has banned certain members in the past of their ability to use that system.)

I think I answered this above

After reading the paper several times to comprehend it, it is evident that the paper stands on a solid foundation of well-established principles, including symmetry breaking and the experimentally verified Meissner effect. The SU(3) gauge symmetry that dominates the vacuum at near-zero Kelvin is a direct result of these mechanisms. It is clear that the approach is not speculative but is instead rooted in robust theoretical and experimental frameworks that are well-documented in physics. Your criticism does not seem to fully engage with the underlying principles being applied, which are both logically consistent and empirically supported. Instead of vague insinuations about a lack of proof, it would be more constructive to acknowledge the established physics that forms the backbone of this work and engage with it in a detailed and substantive manner. The principles used here are not speculative or questionable; they are grounded in experimentally verified phenomena that have direct relevance to the questions at hand

You might want to use a textbook instead of that paper. A quark for example cannot apply strictly SU(3) gauge to describe its interactions but requires the three gauge groups to describe its interactions SU(3), SU(2) and U(1) the quark generations are also involved all quarks do not drop out of thermal equilibrium at the same time nor does each member of each generation. When an atom drops out of thermal equilibrium one can deploy the Saha equations... Hydrogen drops out later than deuterium for example.

lets put it this way from what I read via the Research-gate copy as I don't care to join Inspire are far too few to really describe the theory in the article nor many of its claims. I didn't see any copy that I could confirm is peer reviewed. The copy I read is a preprint. The math inclusive in the article is a more common treatment of the cosmological problem and brief descriptive's of other commonly know equations including its mentions of Snyder's Algebra I honestly don't see any equations specific to the papers theory. ! Moderator Note The article itself has far too many claims not supported within the article in terms of any calculations specific to its claims to be considered an article within the rules required for mainstream Physics . Please review the requirements and rules for the speculation forum given in the pinned threads above.

Interesting conjecture the paper itself seems to be rather lacking in certain details. For example I couldn't see anything I could use to determine an effective equation of state for the cosmological term itself for any means of testability using observation. If I'm missing that could you provide how an effective of state would be derived from the article. I also didn't see how one applies thermodynamic relations such as any pertinent temperature contribution via the Bose-Einstein, Fermi-Dirac statistics so I can only assume what you refer to as an SU(3) atom is and of itself not a particle contribution. It also surprises me you didn't include the relevant equations to the quantum harmonic oscillator in momentum space which led to the vacuum catastrophe. That detail is described under the minimally coupled scalar field langrene.

No true Scotsman fallacy

Ok, I changed my mind: I'll probably look into info about Newton gravity, general relativity, and quantum theory a bit more - and a bit of mathematics related to these if possible too. Sorry about my bit drama manner.