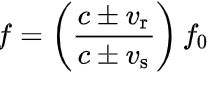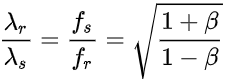Eise

Really? From his article that introduced the theory that later would be named 'Special Relativity': On the electrodynamics of moving bodies I think it is time to close the thread?

Thanks for your proposal, but working all day with computers, and not too far from my retirement (1.5 year), I discover that learning complete new frameworks is a little bit too much. I am working with databases, and am not too bad at it, and in that cognitive frame I am still capable of learning. But for the one or the other formula in Latex, maybe once per 2 months, I would already have forgotten how I did it. But thanks anyway, very kind of you. Best, Eise

(Bold by me) What does 'stationary' mean? Against what? The Lorentzian aether? How can that be, if the LTs do not contain any reference to the velocity of light measured in this 'aether'?

I think I found an even better challenge for you, @externo because it seems you have problems with even simple math. This is the formula for the Doppler effect in a medium: vr = is the speed of the receiver relative to the medium, added to ± (above the division) = if the receiver is moving towards the source, subtracted if the receiver is moving away from the source vs = is the speed of the source relative to the medium, added to ± (below the division) if the source is moving away from the receiver, subtracted if the source is moving towards the receiver And last, but not least: c = is the propagation speed of waves in the medium Now this is the Doppler formula for light, assuming the source and the receiver are moving in a straight line from/to each other: where ß is the usual v/c. Now tell me, where do you see the speed of light in a medium? How do you explain that it does not appear in the formula? The above formula, AFAIK, can be derived from the Lorentz transformations, in which, you probably noticed, the speed of light in a medium does not occur either. Another problem I seem to see, is that you are thinking that relativity has something to do with signal delay. It hasn't. So the blueshift that the observer on earth sees after the traveler has turned around, of course takes time to reach earth. That is just signal time delay, nothing special.

Nope, did not work

Except one (or two?) episodes of 'Tales from the Loop' playing with time, it is not the essence of the series, as it is in 'Dark'. The episodes of 'Tales' are relatively independent, but there are a few running threads through the episodes. But maybe this is not the place to discuss that. Maybe the admins could open a new forum for discussing movies and series? Ups, I did not say that!

Again, no answer. Plugin the LTs in the Minkowski metric, and see what you get.

I had no derivation to check, so I could answer very quickly.

The answer is in your question: animals being eaten are producers and consumers. Pretty useless question.

Did you try 'Tales from the Loop'? Beautiful SF series.

Again no answer. Bye.

Just a tiny remark. As Swansont already said, it is like a chain. Now just 'zoom in into' these chain: it is all EM fields. But you do not ask how all these do work. But the macroscopic magnetic field is not different in this respect. It is just the intermediate of the force, but does no work itself.

Lorentz transformations were derived with the idea that there was an aether and that the speed of light was constant relative to this aether. In order to remove the idea of the ether or at least remove its state of motion, we must add the condition that the speed of light is constant in both directions of motion, unlike classical kinematics. This condition allows us to get rid of the idea of a fixed frame of reference for the universe. Einstein's interpretation is therefore eroneous if there is a preferred rest reference frame for the universe. You did not answer the questions. Looking at all your other postings here, I can only conclude you are discussing here in bad faith. Either answer my questions (and all others that were posed to you...), or I am 100% sure of that.

I am following the discussion a bit, but not precisely. In the end, I am not the expert. Still, I have a question for @externo: Assuming that you agree that the Lorentz transformations are correct, how could they have different results when interpreting them with a Lorentzian aether on one side, and no aether at the other side? Minkowski derived his spacetime metric from the Lorentz transformations, not from Einstein's interpretation. You can try it. Take the Minkowskian metric for spacetime distances: (ct')2 - x'2 = (ct)2 - x2 And then plugin the Lorentz transformations. Do it! It is not too difficult. And? Did you need an aether for that?

Most of Dennett's books, can be read by laypeople, but they are still quite an intellectual challenge. Better to do 'spiraling-in reading': first reading about Dennett, and then read his own books on the topics that interest you. Just to avoid a disappointment. And I completely forgot to give TheVat 5 ups for his OP. As I can only give one point, and I got 4, those 4 van give them to TheVat too. His summary is also great. And without his OP, I might still not have known about Dennett's death. PS Now downloading his book I've been thinking.