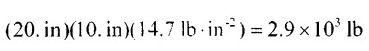All Activity

To give the twin scenario more “twist”, you can allow spacetime to not be flat (GR twin scenario). For even more twist, allow spacetimes that are topologically non-trivial

As KJW has pointed out, the equivalence principle is a purely local statement, meaning it applies only to small spacetime regions - meaning small volumes over short periods of time. Within such regions, there’s no purely local experiment you can perform to distinguish between the two. For the twin scenario, the twin can at every individual instant (or short enough time period) be considered to be subject to a uniform gravitational field, where the gravitational potential may vary from instant to instant. This kind of foliation procedure produces the correct results - though I still don’t think it’s necessarily the best way to analyse the twin scenario.

You are of course always free to pick different coordinates to describe the same spacetime - which is one of the central insights in GR. However, when you do this you also change the physical meaning of those coordinates. In the standard FLRW metric, the time coordinate is chosen such that it corresponds to a clock that is co-moving with the cosmological medium, meaning it fits well with our own physical clocks here on Earth, and thus the “phenomenology” of the metric corresponds to what we actually observe, without any need for complicated transformations. You are free to choose a coordinate system where eg tick rates aren’t constant, but then you need to be very careful how you relate the metric to real-world observations, since the t-coordinate no longer corresponds to Earth-bound clocks. Ultimately it is best to describe the spacetime in terms of geometric properties that are independent of coordinate choice; in the case of FLRW for example, we can say the spacetime is conformally flat, meaning during free fall angles are preserved, but not volumes. These aren’t different “theories”, but simply coordinate choices. You’re describing the same spacetime in different coordinates. KJW has given an example how a “time-only” expansion metric could look like. Ultimately you want to choose coordinates that make your calculations as simple as possible, and that’s often ones based on the cosmological medium. But in principle, the choice is yours, so long as they’re related by valid transformations.

If you can't be arsed to improve the clarity and coherence of your own argument then why should anybody else do it for you? It isn't as if it's a position worth defending.

Your pressure unit is in reality lb force / in2 so the result is not lb but lb force. ie. the force exerted in opposition to the gravitational acceleration of a mass of 1 lb at the Earth's surface. It's a sloppily presented question: lb / in2 is not a correct unit of pressure. g is implicit in both sides of the equation, but cancels.

<yawn>

Well, really, contempt for human life and murdering medical staff does have some parallels with Israel's current tactics which are ignoring clauses of the Geneva Convention (1949, btw) quite thoroughly. I know you are a careful observer of news, so you can't have missed this. But I wasn't trying to make a perfect analogy, just point out that saving lives doesn't require some binary choice where the only choices are mass starvation or an entire city is annihilated. Others here have pointed out that there were other options to bring a Japanese surrender. But those didn't provide a way to show Russia how big a stick we now had. I wasn't saying they were completely noncombatants. No city in Japan could possibly have been so, given the massive national mobilization in that war. Again, I was making a different and broader point - that when you annihilate a city, you will kill mostly civilians, and violate that Geneva clause mentioned above. How can we Americans claim moral superiority over the Japanese if, after condemning them for indiscriminate mass murder, we then engage in same? As an American, I've given this some thought, and I feel strongly that this was a barbarous and shameful chapter in our history in which we cannot claim a moral high road. I will simply not validate Hiroshima and give the monstrous atrocity of a nuclear attack some veneer of moral value. That's a Strangelovian step I cannot make, so we may have to disagree on that.

Guys, why in this question did the question answer only perform the product between area*P to calculate the mass? Question: Answer: Shouldn't the mass be calculated as m = (P*A)/g? Considering that: P = F/A, since: F = m*g P = (m*g)/A P*A = (m*g) m = (P*A)/g By performing dimensional analysis, you can indeed arrive at the value and unit: 2900 lb. However, I don't understand why gravity wasn't considered.

The comments are helpful,the latex and machete,I will try where I can or mayb try to reverse engineer my own ideas and theories,to be on the same table rather than light-years away to avoid a hangman noose. All the same I thought I hand tried to step away from diagrams for simple brains to mathematics...and mayb the input of likes of Mordred, sincerely talking not trivializing others,in my other thread, simplified quantum gravity, he had a lot of input and i had been waiting for him to come back on the forum to just get his take, brilliant brains seems to vanish away with age i.e you can't ask today Higgs a question regarding Higgs boson. and after reviewing my former thread i saw a need for mathematics to bring clarification to my thinking and to tackle Genady on issue concerning geodesic paths and finally settled the issue on faster than the speed of light that unsettled exchemist and others.sometimes whining help but in this form 😂😂😂 or rather 😭 to clean the eyes.

And people can stop moving the goalposts on this too; deterrence ought to mean more than just their use, if it doesn't deter their creation, then eventually they will be used. Nothing is being deterred just delayed. The detterence comes after you use them a bunch, then people forget how bad it was until people are practically foaming at the mouth at the thought of keeping them around and it makes me a little bit sick to be honest. Take issue all you like; if the bombs had went off where your nation was you'd likely feel differently. But because it happened to the civilians of another country/race to you it just doesn't matter? It was ww2 and most of the world was starving, everyone suffered, but it was winding down, they were about to surrender and then the USA released the most cowardly double sucker punch of all time with the highest kill count and for what? A few points scored on a naval base wow and only tons of innocent civilians and two cities as collateral damage? Wow, amazing. This debate is starting to get really boring. Crimes carried out by millitaries need to punish the people giving the orders and carrying them out. Whichever side. Can we all just agree that civilian casualties suck and are unfair without having arguments that amount to "What colour or culture were they? Tell me that so i can decide how much I care." Also where did OP go? Here we are busting our butts having it out and they've gone AWOL!

Have you considered what would have happened if the allies had gone ahead with the alternative plan B of starving Japan into surrender by means of a naval blockade ? The 32,000 POWs and internees held by the Japanese were already on starvation diets - do you think the Japanese authorities would have made any effort to continue feeding those POWs when they were already making contingency plans to starve a significant proportion of their own non-combatant civilian population to death in order to continue the war ? I take some issue with the Gaza analogy too. The Pacific war of 1941 - 45 did not take place in the Middle East in 2024. It took place in the context of a lethal struggle against a violent and well armed expansionist Japan whose military leadership systematically ignored every clause of the Geneva Convention, and exhibited a total contempt for any concept of the intrinsic value of human life - an aggressor that routinely murdered captured nurses and other medical staff (as they did in Singapore in February 1942) and whose soldiers murdered upward of 250,000 unarmed Chinese civilians during a six week killing rampage in the city of Nanjing in December 1937, and also murdered another 150,000 unarmed Filipino civilians in Manila during the Battle of Luzon in February 1945. At a certain point when you are fighting a particular type of enemy, one (as previously noted) with no history of military compromise or surrender in its 2000 year history, then the finer points of moral argument become somewhat moot. You simply have to be prepared to take exceptional measures to break their will to carry on fighting you. I also take some exception to the implied suggestion that the targets selected for the atom bombs contained nothing but non-combatant civilians. Hiroshima was a major military command centre for the Japanese Second General Army in southern Honshu. It also had a large seaport at Ujina that was used as an embarkation centre for Japanese troops, and housed the Army Marine HQ. The city of Nagasaki was likewise a military seaport, and also the home of the Mitsubishi company who were the principal manufacturers of the deadly ‘Long Lance’ (酸素魚雷) Type 93 torpedo used by the Japanese navy throughout WW2. The Mitsubishi Urakami Torpedo Works were in fact one of the military sites that was completely destroyed by the Nagasaki atom bomb. https://www.osti.gov/opennet/manhattan-project-history/images/mitsubishi_image.htm

That's not the part I was calling statistically false. Nuclear weapons have not in anyway deterred the continued manufacturing and testing of nuclear weapons and there are more countries without them who have similarly not been overrun by the powers that do have them so why does anyone need them? It's a circular argument; "Oh we need Nuclear weapons... because nuclear weapons exists, and because nuclear weapons exist.... we need nuclear weapons." As for the second claim you made, that it is letting your guard down to get rid of nuclear weapons, there is only one way to test that out. Get people do disarm and see what happens. Now it's for science and ethics. Great job that's a wrap. See Switzerland. Ukraine didn't get invaded by Russia because it doesn't have nukes, it got invaded by Russia because it used to be part of the Soviet union and the soviet union being made anew is Putins idea of a wet dream.

As before, I''ll use values which produce easily described effects. e.g. 50 Hz A.C. to a 1kW convection heater - the wire to the heater, as well as the heater, will always be warmer than the environment. In this example, most power will be dissipated as IR radiation but a small amount will be 50Hz radiation from the wiring etc. dc current is in practice current which has been constant long enough for transients associated with such as inductive or capacitive reactance to become negligible. 'Instantaneous' is not a meaningful concept for measuring e.g. current (coulombs per second) or power (joules per second) - e.g. 0 coulombs in 0 seconds could be any current i.e. not defined. Calculus, which involves indefinitely small nonzero quantities, is used rather than 'instantaneous' but if applied, everything including inductive and capacitive reactance has to be included. In particular, alternating current in the wire, and magnetic fields will not be calculated as constant even using indefinitely small nonzero quantities. You might better consider dc or ac separately rather than trying to consider ac as 'almost dc.' Or perhaps you just want to consider A.C. circuits where reactance and radiative loss are negligible.

First rule of the speculations forum Speculations must be backed up by evidence or some sort of proof. If your speculation is untestable, or you don't give us evidence (or a prediction that is testable), your thread will be moved to the Trash Can. If you expect any scientific input, you need to provide a case that science can measure I pointed this requirement out to you, and you still did not comply. It’s explained further here https://www.scienceforums.net/topic/86720-guidelines-for-participating-in-speculations-discussions/ Palatability is not an issue; your posts don’t convey any coherent thought that I can discern. I think you overestimate how effective your diagrams are at conveying useful, scientific information.

Anyone else have any comments?

You can disagree, but you need to go some to make the claim that eliminating your nuclear weapons is letting your guard down is "statistically false". It didn't work out for Ukraine, and the jury's still out on any of very few the others that eliminated them. (or for that matter curtailed any nuclear weapons program, for which your argument would at least make some sense)

Only just noticed that there was a mistake. I meant to say emotional phenomenology is fun. Phenomenology is an interesting one because you can study a lot through that lens. Phenomenology of cooking or even hyper specific stuff like The phenomenology of the ghost in literature. One of the few essays I have had to translate myself into English, was originally in Spanish that one.

Interesting.Sadly (or maybe fortunately) I no longer have the intellectual capacity to investigate those questions.I am more or less just fascinated ,for now to learn that that line of enquiry exists .(and prepared to eavesdrop on others who can discuss the subject profitably)

According to Nietzsche (cripes, he had a difficult name!) yes, it does. Almost no-one is capable of greatness, but we should strive to improve the human race so that some day, great men could exist. And I still don't believe he said that a great man has to tell people they're not equal - I think he knew they already knew this. *sigh!!!*

I'd add: learning latex would be a good start. In the photo of math, it's not all oriented the same way as the forum, and being a photo is impossible to properly quote, or dissect for discussion. Nobody is being paid to review your posts, if you want feedback you need to make the interest high and the effort low. I will say your handwriting is very good.

Japanese civilian casualty estimates from Operation Downfall are also much higher. Perhaps they would have unconditionally surrendered or the invasion forces flagged though. There are several ways events could have played out.

I not going to pretend to follow the math. Neither do I want to interrupt where the thread has gone, but I want to bring it back layman speak on my level. Earlier in this thread I did already mention that the FLRW metric is "orientated" where time does not expand with space. I had suspected that a transformation could orientate it differently such that time does expand with space. And I suspected at the other extreme we can have a solution where space does not expand at all and only time does. In another thread I asked about a variable "metric of time", and the "rate of flow of time", which was very difficult to conceptualise and it sort of ended there. My position is that l still maintain the validity of the interpretation that: non-relative time expansion/contraction is indistinguishable from space expansion/contraction. When you look up cosmological redshift in wiki there is no "Temporal Redshift" type. That is, redshift caused by an expanding temporal metric. It doesn't exist. Not a single reference, no studies, no papers. Why? Just because its too complex and abstract compared to space-expansion-only theory? I don't believe complexity is a reason for the entire physics community to shy away from such an interpretation. If it is valid, and no-one has researched into temporal redshift, it can only be because "space expansion" and its universal acceptance has blinded us to the truth that is only one alternative of other interpretations.

It must be related to that weird feeling I get of remorse when I am hungry and remember a random meal from the past and wishing I had eaten it all then, as if that would somehow lead to me feeling less hungry now. Emotional phenomenology is fine. I think that I am feeling and I feel that I am thinking.

The caveat is that nobody has used them against another country but they still are used; it seems like every other year there is a nuclear weapons test going on somewhere in the world and I wonder what the cumalative effect of a nuclear weapons test every other year for few centuries would be. It doesn't change the fact that before long there will be some madman who gets their hands on nukes and isn't dettered from using them, then all arguments in favour of their continued use and not taking as fast of a crawl to global zero as possible, will be moot. There are currently as of January 2023 approximately 12,500 nuclear war heads worldwide that we know of. How many of these going off would it take to trigger a full scale nuclear war and how many need to be used to cause a nuclear winter and irradiating most of the planet? When is the expiration date of effective deterrence of nuclear weapons? No, I'd be more worried about your moral compass if you had no capacity to suffer/desire to avoid it, as then you'd be incapable of empathising with the suffering of others.

Breathing