Linear Algebra and Group Theory
Set theory, groups and ring theory, linear algebra, and other algebra-related topics.
566 topics in this forum
-
Ann and Bill independently work on examples of Cantor's diagonal argument. Ann: 111001... 000111... 101100... 110011... 000110... 010110... transforms diagonal D1 to alternating '01' sequence T1, 010101... which can't appear in any list per the cda. Bill: 000110... 010110... 110001... 000111... 101100... 110011... transforms diagonal D2 to alternating '10' sequence T2, 101010... which can't appear in any list per the cda. If D1 and D2 appear in any list, they must be members of the complete list. T1=D2. I.e. a missing sequence is only relative to an individua…
-
2
Reputation Points
- 168 replies
- 21.7k views
- 1 follower
-
-
In case anyone here hasn't noticed, there have been a lot of debates on this online between people on other forums, some with a good grasp of mathematics and some without. The debate is over whether 0.999 does or does not equal 1. There are many different proofs to prove that it does, but because some people understand some proofs better than others, and some not at all the debates still go on. I've personally been involved in these sort of debates and I can think up at least five different proofs, all based on different sorts of logic, that show that they are equal. The more forms we can find, the better the chances are that someone will understand it. I thought …
-
0
Reputation Points
- 162 replies
- 32.4k views
-
-
Is it just me, or is this whole imaginary number stuff just a bunch of crap? I learned this in Algebra II class the other week. Now, my teacher is trying to apply it. What meaning will this have in my life? Don't get me wrong, I understand the concept...but, why do I need to know this?
-
0
Reputation Points
- 83 replies
- 13.8k views
-
-
After talking with Rev, it became apparent, that I need to review linear transformations. Last night, I spent about 4 hours reading through 3 different books on linear algebra. All I want to do right now, is fully and competently understand what a linear transformation is. Here is where I am at, and would appreciate any help. Ok first of all... The first thing that became apparent to me, was that I need to be able to logically express the concept of "exactly one," as opposed to merely "there is at least one." And I am a stickler about my logic. So for right now, I would like know exactly how some of you address the issue of "exactly one" using symbol…
-
0
Reputation Points
- 79 replies
- 14.7k views
-
-
I need the help of a math's wizard, because I am confused by something.... The odds of winning £10 on the Lotto are 56.7 to 1. Ok. But I have been told that if you write 57 lines of numbers, no matter what they are, you can't always win £10. In fact I have been told that you need 168 lines of numbers to guaranty £10. Could anyone explain the mathematics behind this in simple terms please. I am trying to write a computer program to find the smallest number of lines possible. I also want someone to be able to type 6 numbers into the computer, and the computer will make the smallest number of lines using those numbers. Pincho
-
0
Reputation Points
- 50 replies
- 23.4k views
-
-
My new issue in my journey to try to understand infinity concerns the "ends" of infinity. I was told on here that the infinite sum of 1/2^n = 1, and not just gets close but actually equals 1. I can't help but notice that we are giving infinity a definite beginning point at 1/2 and a definite end point at 1. What could n possible equal to get to this point? If this last point really is a solution to the equation, then wouldn't it have to be 1/infinity, or in other words, the "infinity-ith" point? If so, how can it be said that the natural numbers can numerate all points of a set of size aleph-null?
-
1
Reputation Points
- 47 replies
- 5.9k views
- 1 follower
-
-
I am fixing to start college and I need the best allround scientific calculator. I will probably be doing a little Algebra Geometry and Trig. What would ya suggest?
-
I have found what I think is a simple, possibly efficient, algorithm for a Prime Number Sieve. This sieve is a process of taking a value from the set { 6x-1 U 6X+1 }, (5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37 ... N ). Using that value as a starting point to move through the same of numbers, based a simple pattern that I have found, to mark / eliminate the non-primes. Repeating the process for all the primes. The process using the multiple of 6, a pattern of the odd numbers, & an alternating switch to identify members of the set to be marked as non-prime. The steps of this process are Goto the starting value Inside Loop Add to the multiple the First Constant t…
-
0
Reputation Points
- 45 replies
- 1.7k views
- 2 followers
-
-
given a set with the symbols : " + " for addition " - " for inverse the constants : 1 0 AND the axioms: for all a,b,c : a+(b+c) = (a+b) + c for all a : a+0 = a for all a : a +(-a) =0 for all a,b : a+b = b+a Give a rigorous proof of the following: 1) 0 is unique 2) the inverse of a ,-a is unique 3) for all x,y : -( x+y) = -x +(-y)
-
0
Reputation Points
- 38 replies
- 7.5k views
-
-
Hello! I've worked on a problem concerning even and odd numbers recently...sounds quite simple actually...though I'm not sure whether my (more or less formal) solution is right. It is asked to find out whether there are more even or odd numbers...The result I came to is that there is an equal number of them...How would you solve this problem?
-
0
Reputation Points
- 37 replies
- 6k views
-
-
Recently on a computational engine called wolframalpha, by accident I put this equation for a solution( I wanted a soln of another eqn). But this mistake is not so anymore, it showed me that almost by every mean mathematics can be manipulated. Anyways, the engine showed there exists no soln . for this. I tried this on few others and still got the same. I can't understand this. -1 and 1 both give 1 when multiplied by itself. No square of a number can be in negative form. So sqrt(x)=-1 should have the solution as 1. Can anyone explain this. Also, I searched this on certain sites and they explained with graphs of complex numbers containing p…
-
2
Reputation Points
- 36 replies
- 7.1k views
- 2 followers
-
-
Numbers, why is everyone so stereotypical about thhem. They say 3 "always" comes after 2 and before 4. But why? Isn't it mean to assume that three is always there? I mean, girls got mad when guys were stereotypical about them, why should they be mean to numbers? Numbers have feelings too you know! ____________________________________________________ I did this as a joke, but please still reply as if I'm serious.
-
0
Reputation Points
- 35 replies
- 5.9k views
-
-
I am a bit confused by this. Here is the equation: [math] a=b[/math] [math]a^{2}=b^{2}[/math] [math]a^{2}-b^{2}=0[/math] [math](a+b)(a-b)=0[/math] [math]a=b,-b[/math] let [math]a=1[/math] [math]1=1,-1 [/math] I understand that this cannot be true but why does it work algebraically? To my understanding, if [math] a=b [/math], than [math] a^{2}=b^{2}[/math] but if [math] a^{2}=b^{2} [/math], than [math] a\neq b [/math] What am I not understanding?
-
0
Reputation Points
- 35 replies
- 7.2k views
-
-
Can someone tell me what the origin of zerois???
-
0
Reputation Points
- 34 replies
- 8k views
-
-
What are the axioms of a group? I suspect I know them, but i've read conflicting answers from time to time.
-
0
Reputation Points
- 34 replies
- 6.4k views
-
-
I never understood this concept. What proof backs this up? This argument is sometimes also presented as "2 + 2 = 5 for large values of two." This doesn't make sense to me whatsoever. Can someone please help?
-
0
Reputation Points
- 33 replies
- 8.9k views
-
-
Recently, I have come up with an algebraic structure that I would like to call "Partial rings" with some interesting properties. They are similar to rings, as will be shown later. The rules for this structure are: 1) Group under addition 2) Another function, multiplication 3) mutiplication is distributive 4) multiplication is associative 5 (optional)) Noncommutative group under addition. Some properties already found: 1) The identity under addition annihilates under multilplication (clearly) 2) The additive order of the product a*b divides the additive order of each a and b 3) The set of products is commutative 4) The set of products a*r, r is in R is …
-
0
Reputation Points
- 33 replies
- 7.2k views
- 1 follower
-
-
What is SO(3)?
-
0
Reputation Points
- 32 replies
- 10.7k views
-
-
For example: (1) 3x + 2y + 7z = 100 (2) 21x + 3y - 5z = 50 (3) 4x - 2y + 3z = 20 What is the algebraic method to solve for the sum of unknown variable equaling the number of equations. So if I had 5 unknown variables and 5 equations that included those 5 unknown variables and so on and so on This was my method using a different equation: Isolate x from (1) sub into (2) Isolate y Sub y into x next sub x and y into (3) Isolate z And it worked.
-
0
Reputation Points
- 32 replies
- 6.1k views
- 2 followers
-
-
Consider the following. The Greeks are credited with advancing geometry by large amounts, but consider if one could go back in time and teach Algebra to the ancient Greeks. How would that knowledge hurt their development of geometry and how would it have helped further the advancement of algebra. How would our world be different today?
-
1
Reputation Points
- 31 replies
- 1.1k views
- 2 followers
-
-
Let N = 8765^4321 be writen in decimal notation. If A is the sum of the digits of N and B is the sum of the digits of A, then what is the sum of the digits of B? Have Fun.
-
0
Reputation Points
- 30 replies
- 7k views
-
-
I'm not a mathematician, I'm a very close cousin, a physicist. I've been comparing the idea of a zero from the mathematicians' point of view and the physicists' point of view and find both somewhat incompatible. Maybe the term incompatible seem a little extreme, so allow me to use the term inconsistent. Here goes my argument; Mathematically, if you subtract 2 from 2 what would be left is nothing. This nothingness is what mathematicians call a zero. Physically, If you take away everything, from the largest of galaxies to the smallest of particles, eg gluons, photons, bosons, etc, what would be left? The philosopher would say nothing. The mathematician would say nothin…
-
0
Reputation Points
- 30 replies
- 7.9k views
-
-
This is a question that doesn't have a solid question... Now we use math in everything we do... even on my laptop that I am using for this thread uses mathematics to solve and put in every single pixel on screen... We count words and letters in our language books and count the thousand habitable planets in our solar system. We draw graphs and charts for buisness and the economy needs to know how much they have of anything. But first the big picture. To define everything is like to define 'god'. It is impossble, because we all have a different oppinion or definiton of that. Science has something to do with math. We can't count the amount of atoms that exist in and …
-
0
Reputation Points
- 30 replies
- 15.9k views
- 2 followers
-
-
For matrices, if AB=I, then does that mean BA=I also? If I have 2 matrices and I have AB=I, is that sufficient to conclude that B is the inverse of A? Or do I have to calculate BA explicitly too? I've tried finding a simple 2x2 counterexample but I can't find any. All examples of AB which I've conjured up also have BA=I.
-
0
Reputation Points
- 29 replies
- 22.9k views
-
-
I understand that Minkowski (Poincare?) Space is a Group in Group Theory.(am I right so far?) Well I have (re) learned that for a Group to be a Group there are one or two (4 ?) basic preconditions and that these are (1) that the set must have a operator and (2) must also include an identity element , (3) be commutative in the operations and that (4) each element must have an inverse. Oh and (5) it must exhibit "closure" How do these conditions apply to Minkowski Space? Are the elements of the set spacetime vectors? Are all the vectors unit lengths or can they be any length? What is the operation ? Is the set infinite? Have I got the…
-
0
Reputation Points
- 26 replies
- 9.3k views
-



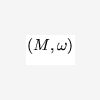


.thumb.jpg.d48da72df0ef44cba163f239ff75b2d2.jpg)
