Everything posted by joigus
-
Number theory derivation from infinity; speculations on equations that are derived in terms of the Field
I'm not sure what relevance this has on Cantor's hypothesis, but the virial theorem is actually more general: True for any potential that is homogeneous in the spatial coordinates: \[ V\left(\lambda\boldsymbol{x}\right)=\lambda^{n}V\left(\boldsymbol{x}\right) \] So ideal gases, harmonic oscillators, and inverse-square systems all have a version of it. Sorry. I mistook this thread for another one. Oops!
-
What is Art?
How about this?: It's any original human-made thing that is intended, not necessarily to serve a practical function, but to engage an audience is sensory, emotional and imaginative dialogue with the artist, and thereby alter their view of the world.
-
Does modern physics support solipsism?
Not that I want to redirect the thread according to my wishes; and despite some very interesting comments having popped up so far, may I insist on my question? Why would it? That is: What is the salient argument from 'modern physics' that would support the view that solipsism is tenable/necessary/etc. in our view of the world? I don't see it. I do intuit that it's to do with quantum mechanics. Namely: that only the mind exists --Wigner's friend and so on. How does physics support that view --or any variant of it that can be explained clearly? Mind you, interpretations of quantum mechanics based on conscience are something of the past, and most of the physics community today find these interpretations at the very least unnecessary, and --given that, and that all consequences of quantum mechanics can be experimentally confirmed and objectively agreed--, unpalatable. Conscience should eventually be explained by science, but not taken as the underpinnings of it. Thinking, or even suggesting that, eg., craters on Mercury that were formed, say, 2 billion years ago, can be explained from the dynamics of the mind, is absolutely ridiculous. But if this complete turning upside-down of the mechanisms of explanation were to be inevitable, very strong arguments, and a theory accompanying them, should be provided. Vague suggestions coming from fancy phrasings of the peculiar aspects of quantum mechanics are not good enough. So I suppose I agree with the OP. I do not believe it.
-
Does modern physics support solipsism?
Why would it?
-
If I was able to live for millions of years
Just to add "cautionary tales of evolution" to what @Phi for All said, The male praying mantis is, in terms of evolution, very successful. Yet, he does it by providing the female with a delicious romantic dinner after sex in which he is the main and only course. Think about the implications of this. Evolution only cares about reproductive success. Doing well for yourself doesn't necessarily matter so much. Fig wasps are an even more extreme example. There are more examples of reproductive champion = individual loser in Nature. In tournament species, successful males are tipically short-lived.
-
The Ambiguity Thread
Thanks, Eise. I think the Dutch --both the language and the people-- are special in many ways, and in a very good way. But ambiguity is certainly no privilege of the Dutch. It's --arguably-- ubiquitous with human communication. It's sure enough present in the animal kingdom too.
-
The Ambiguity Thread
Yes. My rendering: They saw the girl who was carrying carries the binoculars They, with the help of some binoculars, saw the girl They spotted the girl, who was carrying some binoculars They spotted the girl with the help of some binoculars Nice example! First and second: 'saw" = use a saw to cut something Is the ambiguity also in 'zagen' and 'met'?
-
The Ambiguity Thread
Combinations of negative with composite sentences are my favourites. With imperative: 1) Don't just sit there and introduce yourself! 2) Don't just sit around and eat! (Solved with a comma in writing, and with voice modulation when speaking.) With 'because': I didn't marry him because of the money. Nice topic, BTW. I found 4 possible meanings. Some of them are gruesome. One, bordering plain absurd. But nice example!
-
Number theory derivation from infinity; speculations on equations that are derived in terms of the Field
Hi. I'm not an expert, but I can tell you what the present status of Cantor's continuum hypothesis is: (My emphasis.) https://en.wikipedia.org/wiki/Continuum_hypothesis So, within the Zermelo-Frenkel set-theory axioms, plus the axiom of choice, you can neither prove nor disprove the continuum hypothesis. And that's what I know. The possibility of a cardinality sandwiched between aleph_0 and aleph_1 is still conjectural.
-
What are you listening to right now?
What's eternal, is, even if it lasts for a minute.
-
Examples of Awesome, Unexpected Beauty in Nature
Awesome.
-
"AmmoniaConcentration" package in 'R'
I stand corrected. It sure looks a lot like the Henderson-Hasselbach equation. The base-10 logs should've given me a clue.
-
Jesus and Muhammed, same person?
Tell you what. Why not taking it further still? Zoroaster didn't die, so he was immortal. He became Jesus, who became Mohammed. That works better, I think. Covers more history, and explains monotheism as a logical continuity. IOW, The funny thing about religious thinking is you can make up just about anything. It all seems to work in your mind, under the utterly permissive protocol of coming up with a convenient just-so story, which is what characterises religions of any kind.
-
"AmmoniaConcentration" package in 'R'
I know the answer to the 1st one: It's the linearised Arrhenius equation: https://en.wikipedia.org/wiki/Arrhenius_plot which relates pH, pka, and activation energy with absolute temperature. I hope that helps.
-
Sufficient conditions for a critical point at (a, b, c)(i-e) [math]\nabla {f}(a,b,c)=0[/math]
In the theorem's case, it's important to realise that, \[D=\frac{\partial^{2}f}{\partial x^{2}}\frac{\partial^{2}f}{\partial y^{2}}-\left(\frac{\partial^{2}f}{\partial x\partial y}\right)^{2}=\left|\begin{array}{cc} \frac{\partial^{2}f}{\partial x^{2}} & \frac{\partial^{2}f}{\partial x\partial y}\\ \frac{\partial^{2}f}{\partial y\partial x} & \frac{\partial^{2}f}{\partial y^{2}} \end{array}\right| \] In the case you propose, \[ \left|\begin{array}{ccc} \frac{\partial^{2}f}{\partial x^{2}} & \frac{\partial^{2}f}{\partial x\partial y} & \frac{\partial^{2}f}{\partial x\partial z}\\ \frac{\partial^{2}f}{\partial y\partial x} & \frac{\partial^{2}f}{\partial y^{2}} & \frac{\partial^{2}f}{\partial y\partial z}\\ \frac{\partial^{2}f}{\partial z\partial x} & \frac{\partial^{2}f}{\partial z\partial y} & \frac{\partial^{2}f}{\partial z^{2}} \end{array}\right| \] The condition that these 2nd-order determinants not being zero amount to being able to invert the relation that gives you the second-order derivatives and ascertaining the nature of your critical point. The determinant being zero amounts to second-order equations not being solvable, and therefore the method being inconclusive. There's an elegant method to solve this kind of problem which is the method of Lagrange multipliers. And there's the method that @Genady proposes too.
-
Maxima and Minima (vector calculus)
Sorry. I meant the next-to-zeroth-order correction. If you Taylor-series expand you immediately see it's a maximum, because there0s no 1st-order correction and the 2nd-order correction is negative. That's what I mean, and sorry for the confusion.
-
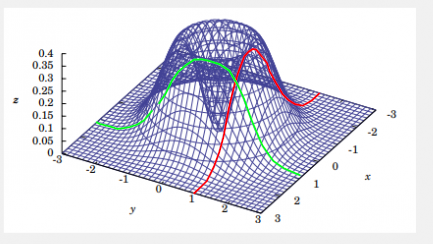
Maxima and Minima (vector calculus)
https://www.wolframalpha.com/input?i=plot+(x^2%2By^2)exp((-x^2-y^2)) The intuitive idea you can get from highlighting x=1 and y=1 curves: And another analytic tool is using polar coordinates, \[ \left(x^{2}+y^{2}\right)\exp\left(-x^{2}-y^{2}\right)=r^{2}\exp\left(-r^{2}\right) \] and then do a Taylor-series expansion around r=1 in a small positive parameter \( \varepsilon \), \[ r=1+\varepsilon \] \[ \varepsilon>0 \] \[ r^{2}\exp\left(-r^{2}\right)=\left(1+\varepsilon\right)^{2}\exp\left(-\left(1+\varepsilon\right)^{2}\right)=\left(1+2\varepsilon+\varepsilon^{2}\right)\exp\left(-1-2\varepsilon-\varepsilon^{2}\right)= \] \[ =e^{-1}\left(1+2\varepsilon+\varepsilon^{2}\right)\exp\left(-2\varepsilon-\varepsilon^{2}\right)= \] \[ =e^{-1}\left(1+2\varepsilon+\textrm{order}\left(\varepsilon^{2}\right)\right)\left(1-2\varepsilon+\textrm{order}\left(\varepsilon^{2}\right)\right)= \] \[ =e^{-1}\left(1-4\varepsilon^{2}\right)+\textrm{order}\left(\varepsilon^{2}\right) \] And, as you see, the first-order correction is negative no matter what orientation with respect to the origin (just where the bump is) you place yourself. Same goes for 1-epsilon, of course.
-
What computers can't do for you
Great topic that deserves more attention, though I'm glad it got the one it did. I don't know if my comment will be useful, but I'm thinking of chess as an interesting testing ground. Computers have far exceeded the capabilities of human minds. Computers play only on the grounds of pure combinatorics. Grand Masters, on the contrary, although they have powerful combinatoric minds by human standards, at some point through the complexity of the game, they must base a significant part of their reasoning on strategic, conceptual principles rather than pure if-then sequences. Strategic principles can deal with wide classes of combinatoric landscapes with the result of improving your chances of winning only on the average. It is not entirely impossible that computers get so good at calculating outcomes that the make our pattern-based reasoning obsolete. It is entirely possible that if we insist on computers being conceptual, we'll force them to play on somebody else's turf. On the game vs task discussion; I see no difference at all. But maybe I haven't thought about it hard enough.
-
perpetual motion machine (split from topic of the same name)
We can only hope.
-
perpetual motion machine (split from topic of the same name)
JamesL's trajectory on SFN is the closest to a perpetual motion I've seen here. Two cycles and counting... Plus perfect experiment on shooting yourself in the foot.
-
perpetual motion machine (split from topic of the same name)
Did you say 'ta-ra'? Sorry, that was a cheap joke. Thank you for providing evidence that it doesn't work --as exchemist has explained. I would also demand of any claim that any of the thermodynamic principles fails, a complete thermodynamic explanation, as well as a thorough examination from mechanics, or field mechanics, or quantum mechanics if need be; of why that thermodynamic principle fails, or an exception is met in that particular case.
-
Why is red hair unattractive in males, but neutral or attractive in women? Is there an evo psych explanation?
I agree --from every bit of evidence I know about. I think the reason underlying it is behaviour is very heavily influenced by environmental factors and ongoing processes in the mind --recent memories, interrelation/correlation of stimuli... In order for a recognizable pattern having a nearly 100 % molecular basis to reflect in behaviour --in the form of a fixed action pattern*, quite independently of those passing processes-- one seems compelled to think in terms of something really wrong in the genes or regulatory sequences, etc.--what I mean by 'molecular.' Otherwise, it's just too iffy. *I'm thinking OCD, PTSD, etc.
-
Why is red hair unattractive in males, but neutral or attractive in women? Is there an evo psych explanation?
What I mean is that some particular behaviours can be traced back to a molecular basis, at least partially. This is especially true of some behavioural disorders. Some of them have a genetic basis, others can be partially explained by imprinting coming from environmental factors that get more or less permanently registered. But I'm talking here with a certain amount of diffidence, as I'm not an expert. I'm not aware of any molecular mechanism having been shown as being at the basis of sexual selection.
-
Why is red hair unattractive in males, but neutral or attractive in women? Is there an evo psych explanation?
References? The OP is basing the premise on a social perception (my emphasis): Unfortunately there aren't, to my knowledge, any salient features results/mechanisms of evolutionary biology that allow one to talk with any degree of confidence on how this or that peculiarity "is regarded" this or that way. I don't think, for example --and correct me if I'm wrong-- that sexual selection has been understood to the point of being related to molecular bases, or even to evolutionary dynamics in the way of population dynamics, etc.
-
War Games: Russia Takes Ukraine, China Takes Taiwan. US Response?
Now that Mistermark has left for a couple of weeks, There's still an echo of bells lingering in the air, sounding, Chamberlain, Chamberlain..., The politics of throwing the dog a bone. It's not like it hasn't been practiced before, It's not like we're clueless about the horrours it brought. Megalomania is easy to diagnose, and we know the profile very well. Putin is a shameless narcisist, and that's plain to see. He plays dominant male primate to a tee.