studiot

I don't see any justification for the first statement, (Which is think is wrong because of carries as below) I don't understand the second statement at all. The following beginning analysis may help, Start with two nine digit numbers XXXXXXXXX and YYYYYYYYY. Allow all digits 0 through 9 including leading zeros, which will take care of the possibility of the actual numbers having less than 9 digits. The last digit is a zero so consider all possible pairs that can result in a zero. Strike out those that have a factor from the disallowed list. [math]\begin{array}{*{20}{c}} {Pair} \hfill & {Divisor} \hfill \\ {\left\{ {0,0} \right\}} \hfill & 2 \hfill \\ {\left\{ {1,9} \right\}} \hfill & - \hfill \\ {\left\{ {2,8} \right\}} \hfill & 2 \hfill \\ {\left\{ {3,7} \right\}} \hfill & - \hfill \\ {\left\{ {4,6} \right\}} \hfill & 2 \hfill \\ {\left\{ {5,5} \right\}} \hfill & 5 \hfill \\ \end{array}[/math] Hence the last digit (of each number) can be chosen in 2 possible ways (as Tina says ) but However since both add up to 10 there must be a carry to the next digit. Also all possible last digits are now odd so from no on no number will be divisible by 2. Since there is a carry, the two digits must add to 6 or 16 Listing these as before [math]\begin{array}{*{20}{c}} {Pair} \hfill & {Divisor} \hfill \\ {\left\{ {0,6} \right\}} \hfill & - \hfill \\ {\left\{ {1,5} \right\}} \hfill & - \hfill \\ {\left\{ {2,4} \right\}} \hfill & - \hfill \\ {\left\{ {3,3} \right\}} \hfill & - \hfill \\ {\left\{ {8,8} \right\}} \hfill & - \hfill \\ {\left\{ {7,9} \right\}} \hfill & - \hfill \\ \end{array}[/math] Which yields 6 possible pairs, not 3 as Tina hopes I will leave it to you to decide if any further divisors can be eliminated

The point is that prime no prime number greater than 23 is divisible by any of the first 9 primes. So each prime number and its pair which adds to make 223092870 will be candidates for inclusion and so must be checked. and there are a great many prime numbers up to 9 digits long. But added to these are numbers which are not prime yet still not divisible by any of the first 9 primes such as the example 2419 I gave. All of these must also be checked.

Why are you suprised? Yes, you made a valid comment that the problem is ill defined. But you also made an invalid one about irrational numbers in your examples. Yes I also made an invalid one, which joigus picked up and I immediately corrected. We all make mistakes; we all need to admit them. Well this is one very long way to do it since that is only a beginning, not a solution. There are plenty of primes less than your criterion for example the 1,000th prime is only 7919 Further there are other non prime numbers not divisible by your set eg 2419 is not prime nor divisible by your set.

Counterexample: π is irrational; 1−π is irrational too. but π+1−π=1 . Nice one. +1

I did look at this one, but I am sorry to say that all of us have parts of our subject we like more than other parts. And amongst my personally least liked parts are combinatoric and number theory. There seem to be several problems of this type going around at the moment. On another (maths) forum they have been debating this simpler one for a couple of weeks now. and this is only a four digit number. The one here is a nine digit number so I would expect candidate numbers for addition to be of the form xxxxxxxxx + yyyyyyyyy Which has a lot more combinations. This really is problem that lends itself to a computer solution so I am suprised at Sensei's response, which is incorrect. since the last digit is a zero, there must be a carry so possible choices for pairs in the last positions are [0,0}, {9,1} , {8,2}. {7,3), {6,4} and {5,5} So {x,y} can be selected in 6 different ways. But any number ending in a 5 is divisible by five so the last one can be discounted. Further reduction can be had by noting that any pair containing an even number can be discounted as divisible by 2, another orignal factor. You can work through the digit pairs to find out how many possibilities there are for each other pair. Then multiply these together an see the final result, using the laws of combinatorics. Tina please note this first result and compare with your answer. I don't think there are any two irrational numbers that can be added together to make a rational one. In any case none of these are irrational.

Trying to post a Cayley table [math]\begin{array}{*{20}{c}} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}[/math] [math]\begin{array} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}[/math] [math]\begin{array}{*{20}{c}} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}[/math]

I can see my table in the list in the activity tab, but I can't see it in the thread itself. This is even after refreshing the thread in the normal manner for MathML. [math]\begin{array}{*{20}{c}} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}[/math] [math]\left( {\begin{array}{*{20}{c}} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}} \right)[/math] [math]\begin{array} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}[/math] [math]\left( {\begin{array} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\ \end{array}} \right)[/math]

[math]\begin{array} + & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \\\end{array}[/math]

Here is what is inside the front cover of a typical computer book. I assume since you have your book you can find something similar. It not only details the rights and restrictions for the reader, but also acknowledges where the authors used software to generate example pages for the book and example screens from real life.

This is the last thing you should do. Wiley or its subsidiaries are under no obligation to reply to you. Period. You, however, owe the actual copyright holder a duty of diligence to respect that copyright. Copyright arises automatically at the moment of creation of the work. There is no requirement on the creator to announce his or her copyright. If they chooose to do so or hand it to a publisher or other person they may do so. Wiley will certainly have stated the rules of use or restriction on the copyright at the very beginning of the book. However with textbooks that state their aim is to tell you how do do something, their is implied tranfer of enough copyright to perform whatever they tell you. So in a maths book if they said "to add 3027 to 5144 place one above the other and draw a line under the stack. Then add each vertical pair of digits, with carries, starting from the right hand side to form the sum placed under the line," you would be OK to do this as often as you wish. The same if they showed you how to code a macro in Word or use the command line editor. If however the author states in the preface something like "there are new results, never before published" you should at the very least write to them explaing your interest and offering to include an acknowledgement as the originator. Remember you can't copyright an actual idea, only a specific presentation of it.

+1

So you thought that the rules of both politeness and this forum don't apply to you ? A response typical of those ignorant of the subject they are espousing.

My dog changes from somnolent to very intelligent and communicates most successfully with me every mealtime and walkies time.

I would suggest the way the question is phrased misses a trick from our own historical experience. You suggest one language, and each language on Earth is unique because it doesn't need to be otherwise. Yet it is known both from deciphering codes and the experience with the Rosetta Stone that having more than one different representation of the sme thing in the single most useful thing to have. Consequently our communication attempt should contain not one, but many, 'languages' for comparison. Edit cross posted this this. +1

You introduced a Mars Rover. I asked you two straightforward uncontroversial questions and provided quite a bit of useful information about both planetary thermodynamics in general and its application to both Mars Rovers and this thread. You have failed to respond. Is there a problem ?

Did you say you were some sort of engineer ? Surely you understand that engineers use parameters that are single numbers to describe an environment or regime for instance Reynold's Number in fluid mechanics distinguishes between quite different mechanical environments in fluids. In the same way the average surface temperature can form part of another dimensionless environment number ( Xi) that indicates whether a planet has an atmousphere at all and, if so, what the gases are likely to be. [math]\Xi = \frac{{3{k_B}T}}{{4\pi G{r^2}\rho u}}[/math] where kB is Boltzman's constant, and u is the atomic mass unit = 1.66054 x10-27 kg Ref Douce : Thermodynamics of the Earth and Planets : Cambridge University Press. Douce gives a derivation and interpretation of Xi for all the planets and some moons on pages 616 -620 The other informatom contained in this parameter, I would suggest would be very useful for someone designing a rover as it contains the gravitational potential energy at the surface, (That is it compares the gravitational potential to the escape kinetic energy via Boltzman) Which I would think very useful in stability/ traction and other mechanical considerations for a rover, apart from the obvious materials considerations of the operating temperatures such as brittle transition temperature/ phase change temperatures etc etc. What were you saying about climate change and what does that have to do with a mars rover ?

Wouldn't it be nice to get AJB back, that's his field. Please note the ability of this site to do subscript and superscript This is unusual even in scientific and maths forums. Look for the x2 and x2 on the entry editor tool bar.

Well you really have got me there. What on earth do you mean ? 6 dimensions of the box?

I think there are already too many vagaries in this thread.

Have you not answered your own question ? Surely the average is useful for some purposes but not for others in both cases. So clearly knowledge of the value of that average alone is worthless without knowledge of the intended use. I see that you joined 13 hours prior to this post and have already made 5 posts here. Welcome, but I expect you don't realise that new members are allowed only 5 posts in their first 24 hours. After that they can post normally. This is a (sadly) much needed anti spam measure So I look forward to your clarification of your topic in around 11 hours time. I don't agree that this conclusion follows from that premise for either the car or the Earth's average 'temperature'. Both contain internal heat sources.

To continue where I left of and pick up and develop joigus points about limits The f(x) and y =y(x) notation comes in useful if you want to get it all onto one line so the derived functions become f'(x) and y'(x). This is not directly related to any of the d notation variants and also becomes very clumsy when many variables are involved. So let us look at the d notation, which is, after all, what you are asking about. So we have Greek capital delta [math]\Delta [/math] Greek lower case delta [math]\delta [/math] Roman Capital D Roman lower case d Eighteenth century European stylised script d [math]\partial [/math] We have all of them because each perform a different operation (remember them) on the symbol that follows them. The first one is not important to us because we use it for the difference between two specific values of the variables represented by the symbol that follows. So the difference in height, [math]\Delta h[/math], between the ground and the gutterline of my house is 18 feet. [math]\Delta h[/math] may be large, but must be exact. That is it is a number. As it is a number it can legitimately be zero. The second one is important to us because it is not only about small differences in the values of the variable that follows it, it is about arbitrarily small differences. This means that [math]\delta x[/math] is not exact but may be made smaller and smaller indefinitely. So it is not a number it is a sort of function. Also since it is not a number it can never be zero, since zero is a number. This brings us neatly to the idea of limits. This is a sequence [math]1,4,9,4,16,...[/math] If we put in addition signs it becomes a series [math]1 + 4 + 9 + 16...[/math] And if we work out the differences between each term or the changes from term to term [math]3\quad 5\quad 7[/math] The three dots at the end is the convention for continuing indefinitely. It can immediately be seen that all the values for both the sequence and series and for the differences increase with each additional term added so each get larger and larger. This is called divergence and the sequence and series are called divergent. Such series do not have limits. If however we take the reciprocal of these sequences they get smaller and smaller, whilst the partial sums for the series gets closer and clsoer to a specific number (1.64) [math]\frac{1}{1} + \frac{1}{4} + \frac{1}{9} + \frac{1}{{16}} + ...[/math] [math]1 + 0.250 + 0.111 + 0.063...[/math] [math]0.75\quad 0.139\quad 0.048[/math] This behavious is called convergence. The specific number is called the limit. Because the process can continue indefinitely we write [math]\mathop {\lim }\limits_{n \to \infty } \sum {\frac{1}{{{n^2}}}} = 1.64[/math] Next time, this will lead directly into the limits [math]\mathop {\lim }\limits_{\delta x \to 0} [/math] and [math]\mathop {\lim }\limits_{\delta x \to 0,\delta y \to 0} [/math] So we have numbers, functions, variables, operators, limits sequences and series all mentioned before. An easy way to look at operators are that simple functions work on numbers to output other numbers and operators work on simple functions to output other functions. You will need to do some work on these to use all the to get a handle on what calculus is, what it can do for you and what it can't do for you. So please let us know any ideas in this development you didn't get a hold of properly so we can help correct that.

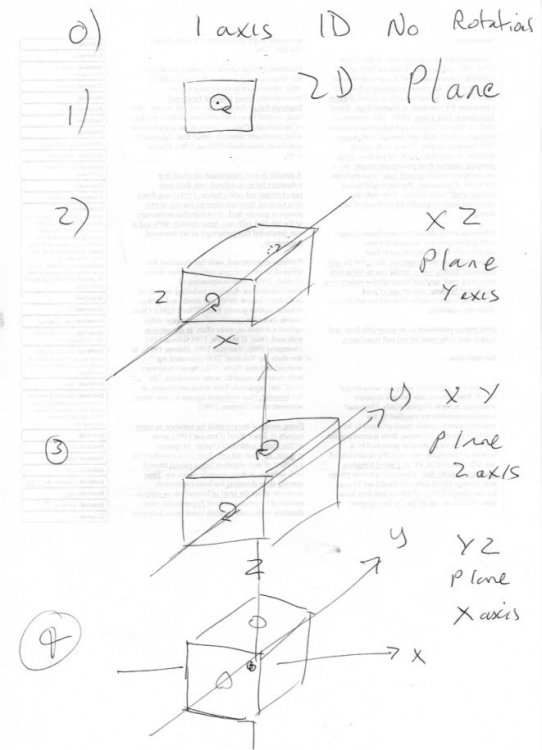
Gosh you are a hard person to keep up with on ideas. I see you have started another thread this morning. I seriously recommend you at least get to a sensible pause point with each one before moving on, we still have a long way to go in your calculus one. Anyway swansont has answered your question but here is more on my comment. Here is a brilliant experiment you can easily perform to gain insight. You will need a cardboard box with all six sides intact. Here is a quick blackboard sketch. Rotations can be represented by complete circles. Consider first one single space dimension. There is nowhere for rotations to occur. You have to leave the dimension (employ another one) to even turn around. This is Fig 0. Move up to two dimensions _ I have modelled this as a plane in two dimensions in Fig 1 You can have a rotation about any point in the plane. Draw this as a circle on one face of your box, as in Fig 2. But any rotation is about an axis which has to be a line in a third dimension. So if you extend a line through your point through the opposite side you have the z axis. You can draw a circle round it though any plane parallel to the first side like the opposite side. Now move up to 3 dimensions. You have to pairs of sides you can draw rotation circles on to generate two more axes, making 3 in all. As in Figs 3 and 4. I have shown the conventional right handed rectangular xyz coordinate system. Now comes the clever part - your experiment. Use the box to convince yourself that rotation on any plane at any angle has an axis within the 3D system. You do not need to leave 3D and have a rotation axis pointing into a fourth or higher dimension. This is what I mean when I say that 3D is complete for rotations. Let us know how you get on with your box.

I'm sorry to have to tell you that your video is a sorry mixture of fact and fiction that reaches some startling unsupportable conclusions. You will only confuse yourself at best and start to 'believe' junk Physics if you try to study from stuff like this. You question is, however a valid one that is worth a considered answer. The third spatial dimension is necessary in our physical world to achieve closure for a set of rotations. This is also why a fourth spatial dimension is not needed and we do not observe one.

Yes this is a profound statement and very important in calculus and analysis more generally. This was why I said that dx on its own is meaningless. Yes a limit has one numeric value, if the limit exists at all. But this x can never = 0 statement is not right as it stands. We will come to a proper version in due course. But first some background, that will become increasing useful as things progress. Note the author says that Analysis is mostly limis and calculus, but it also includes stuff about functions, sequences and series which are necessary to move on from the algebra of quadratic equations. So let us start with variables and functions. You will be please to hear that we don't need the whole apparatus - That can take a whole semester by itself - just some of the bare bones. So variables. A variable is perhaps the most self evident word in Mathematics. It really does exactly what is says on the tin and no more. A variable is something that, well varies. More precisely it may take on many different values. And a numeric variable is a variable whose value is numeric. Your x is a (usually) numeric variable. So what values can a variable have ? Good question, note I may take on, not does take on. The question is incredibly wide since all we know is that the value of our variable is a number. So any value between plus and minus infinity will do. Enter the mathematical function to the rescue. The main part of a function is a rule or equation or other expression for obtaining (numeric) values. Other parts limit the actual numbers we are allowed to use. So the square root function excludes all negative numbers. That still leaves a lot of numbers available. Since x is a variable, we can expect most functions of x to also be variables. We put different numbers in and expect to get correspondingly different numbers out. An exception to this is called the constant function. You get the same number out, whatever number you put in. OK numbers in ; numbers out. We now have two variables, x and f(x) and we can start going places. I have said f(x) since you have used it. But I am now going to change to y = f(x), which is using the rule to define the function as most folks do. So the next thing to understand is that x and y or f(x) are two different types of variable. x is an independent variable, which means that we can put in any number we are allowed. y = f(x) is called a / the dependent variable because its value depends upon the both the number we put into x and the rule which generates y. Having swallowed and digested all this guff we know enough about variables so are now ready to examine all the types of the 'd' in dx. 'd' is called an operator. An operator performs some process on the variable it operates on - in this case the variable x. This is the reason for changing from f(x) to y. We can operate on y with 'd' to get dy. We will tackle that next time, but a question of you if I may. Another person in another forum has asked a very similar question. Have you any relation to Idon'tknow, elsewhere ? I want not mix up answers to each.

I downloaded the third edition and I can't say I'm suprised you are confused if you are really using this book to learn the differential calculus. In particular my edition does not contain 'x' on page 7, 8 or 9. I asked you what you thought 'x' is because all those comments of yours that I have quoted suggest to me you don't understand this. It is vital that you do understand since 'x' is not a number. In arithmetic/algebra 'x' often stands for an unknown number that is to be determined In calculus 'x' is something else entirely and the book uses it in this way, but does not explicitly make this clear. 'x' is a variable. So that is where we should start. Do you wish to go on ?