studiot

Again some history (of mathematics) books publish timelines, These can also be a valuable source of information and inspiration.

A couple of things to add to swansont''s excellent post. Firstly Thermodynamics largely ignore the time variable. In particular it says nothing about how long a system will remain in a given state or how long it will take to reach that or another state. So these so called second law violations are 'instantaneous' and short lived, but the second law always wins on a time averaged basis. Secondly what makes you think these are actually formal 'states' ? Formal states have state variables that are properly defined. You cannot apply most of classical thermodynamics to improperly defined states.

I think I get the general idea. +1 for ambition, I will remember to log on again in 3020 to find out how you got on. Meanwhile here are a few thoughts. If you have access to a library look at the contents pages of compendia of mathematics books. I have a couple by that name, one by Manzel (2 vols) and one by Meyler and Sutton. There is also the Princeton Companion to Mathematics and the Cambridge Encyclopedia of Mathematics. The contents pages should give you some subject headings to think about. Also some authors publish dependencies or dependecy diagrams such as "chapters 4 -7 should be read before chapter 11". though this is more common in Engineering than Mathematics. However such information from either subject could be very useful, as it shows what depnds on what. As regards the subject areas themselves I suggest you don't use the tree analogy. This reuqires that the 'branches' are separate areas or subjects. In truth there is considerable overlap and I don't thionk there is a single 'branch' that could stand alone by itself. There is considerable overlap, For instance although Geometry does not require measurement, you could not do Geometry without numbers even for shape and form. How else could your distinguish triangles, squares, pentagons hexagons etc? So I suggest you go for a tiled presentation, perhaps a bit more formal than in Ghedieons diagram (+1 for finding that). With suitable overlap or overlay you can sowh the interactions. Go well in your endeavour.

I am not, and never have, disagreed with your outlining of basic mathematical set theory in respect of the word 'partition'. This is one reason why I have tried to avoid using the word since its use in classical thermodynamics is somewhat different. However the devil is in the detail as always. You are quite right to identify STRUCTURE and marking out differences between sets with the same Mi. This is the point I have been trying to make. However you have missed one important point. Mathematical partitioning of Mi (is based on) equipartition and implicitly assumes the 'equipartition theorem' of thermodynamics. You have also mentioned disjoint partitions, which is important in the mathematical statistics of this. STRUCTURE, as observed in the physical world, creates some stumbling blocks to this. I was hoping to introduce this in a more measured way, but you have jumped the gun. As I said before, we both mentioned Turing so suppose the tape running through the machine includes the following sequence ........1 , 1 , 1, 0, 0, 0...... STRUCTURE includes the possibility that the first 1 in that sequence can affect the entry currently under the inspection viewer of the machine. Disjoint require that it cannot. So a Turing machine cannot analyse that situation. Nor can it arise in information technology, whose partitions are disjoint. The anomalous behaviour of Nitrogen etc is an example of this, as already noted. The interesting behaviour of Nitric Oxide, on the other hand provides an example of a genuine statistical two state system behaviour. Finally, I do hope, you are not trying to disagree with Cartheodory. However you come at it, statistically or classically, you must arrive at the same set of equations. And you seem to be disagreeing with my classical presentation, because it is much shorter than the same conclusion reached in the statistical paper you linked to ?

I'l just answer this one for now since it is an example of Caratheorory's formulation of the Second Law. You have correctly anticipated part of my answer. I do think our discussion is beginning to get somewhere now. +1 Perhaps you have come across this? Anyway here is an analysis of the system Suppose that when the piston is at the position shown, the system is in equilibrium. So the left hand chamber equilibrium volume is VA and the right hand volume VB. For the subsytems (partitions in your parlance) nearby states have volumes (VA + dVA) and (VB + dVB). So their entropy changes are [math]d{S_A} = \frac{{d{E_A}}}{{{T_A}}} + \frac{{{P_A}}}{{{T_A}}}d{V_A}[/math] and [math]d{S_B} = \frac{{d{E_B}}}{{{T_B}}} + \frac{{{P_B}}}{{{T_B}}}d{V_B}[/math] But [math]d{E_A} = - Pd{V_A}[/math] and [math]d{E_B} = - Pd{V_B}[/math] so [math]d{S_A} = d{S_B} = 0[/math] Therefore [math]dS\left( {system} \right) = d{S_A} + d{S_B} = 0[/math] So the entropy is the same in all positions of the piston. Thank you for the link I have downloaded the paper for later reading. I am glad you mentioned Turing because his machine is the crux of the difference between information entropy and the entropy of physical systems. So I will come back to this.

I don't understand. I quoted directly from your post before your last one. But my comment was a bit cheeky. I simply meant that thermodynamics was developed to enable us to predict (and therefore use) the time evolution of systems, including boxes of gas. It was not a criticism. Salt and pepper are part of the ncessary scientific apparatus for this. Take a sheet of paper and shake out some ground pepper over it. Mark where each grain falls on the paper. Dust off the pepper and take a ruler. You will find that a random ruler line matches the position marks of some of the pepper dots. Leylines are not magic. (I believe you recently referred to someone's experiment with random chords)

I really don't understand what you are getting at here. I am not saying the thermo partition is the only one. Quite the reverse. That is the whole point about my flats and pigeonholes analogy or chessboard squares, that you have yet to understand. Perhaps this statement of yours will help since I am matching the flats/pigeonholes or squares as a definition of particular classes (not of equivalence classes in general but different ones) There is a one to one correspondence between the state structure in thermodynamics systems following Boltzman's distribution and some information systems. Of course there is, the layout of available 'boxes' follows the same law for both. But the use of this is different and there are other laws which also apply to one or the other individually, which are different. Can you point to an emergent phenomen in information theory? I can offer you one from the physical world, that as far as I know, has no counterpart in informatuon theory. You have answered my question rather briefly Can you point to a QM law applied to information theory to produce QM effects in information behaviour? I am listening out for your detailed explanation of the anomalous ionisation energies and its alleged counterpart in informatuion theory. I am sorry if I misunderstood you but that was the impression I gained reading your previous posts. If I did please consider that other may do as well. However if you now confirm your view that two structures may have some similarities or identities but also some differences. I can happily accept that. My point then becomes, you cannot (necessarily) separate off the differences and declare them identical. Though you may, of course, take advantage of the similarities in using one to model the other. Hopefully the above now puts my view on this into context. Just as you have said that you didn't say there is only one law, I didn't say that all the laws of thermodynamics are different, I claimed that some are the same and some are different. Can you now offer me the same courtesy? In relation to this, have you hear of the division into "The Relations of Constitution" and the "The Conditions of Compatibility" ? If not it might pay you to study them a little. They are an important way of analysing things. @Tristan L and @joigus Surely that is the point of Thermodynamics - To model what a box of gas is going to do ? However I have not been following the runes example very closely, but perhaps I can offer my 'salt and pepper' set explanation of Leylines here ?

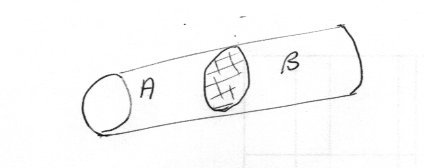
Here is another simple problem Suppose you have a sealed adiabatic tube containing an adiabatic frictionless piston dividing the tube into two chambers, A and B as shown. Let both sides of the system contain an ideal gas. Discuss the time evolution of the system in terms of entropy.

And I'm sorry to point out that you seem to me to be bent on finding fault with my attempts to explain my principle point to you, rather than understanding the point itself. As I understand your thesis here, you are proposing that there is one and only one Law or rule that applies to your partitions, that due to Boltzman. However it remains your responsibility to support your thesis so please explain the anomalous first ionisation energies of Nitrogen, Phosphorus and Arsenic in terms of your proposition.

This is the unaswered question. +1 Consider a system of molecules in some volume. Unless both molecules have the same velocity they do not have the same kinetic energy and therefore the internal energy is not evenly distributed between the molecules (maximum entropy). So the famous 'hot death' of the universe must be a static (as in unchanging) situation from the point of view of maximum entropy. But this view ignores the fact there are twin drivers in the thermodynamic world that often pull in opposite directions. The principle of minimum energy can be used to devise a system that will oscillate indefinitely at fixed (maximum) entropy.

Thank you for considering my comments. I'm sorry my analogy was not clear enough for you to understand. So try this one instead. Both chess and draughts are played on the same board. But they are very different games with very different rules, and different end results. Events can happen in chess that cannot happen in draughts and vice versa. The same can be said of the partitions of your master set. This carries over to the other part of your answer. There are umpteen relationships in physics where something is proportional to something else. And very often the contant of proportionality carries the units as in strain (a dimensionless quantity) is proportional to stress. But that does not mean we can disregard the constant and say therefore stress and strain are the same as thermodynamic entropies. Otherwise you could model one on the other, but if you tried you would obtain conflicting results, just as if you tried to play chess with a draughts set or vice versa. Information entropy and Thermodynamic entropy are not the same, or subject to the same laws (as in the rules of chess and draughts).

Didn't you miss something out here? Thermodynamic entropy has to have units of energy per degree of temperature. Other entropies, such as your runinations (pun intended) will have different units. In a block of flats there is (or should be) a one-to-one between the pigeonhole letter boxes at the entrance and the flats and their organisational structure. But would you rather live in a pigeonhole or flat? They are not the same.

If you are interested the extract was taken from Professor Frankel's book "The Geometry of Physics" : Cambridge University Press This is a large encyclopedic tome that covers a huge amount of ground from the topology of Kirchoff's laws to the most modern versions of GR. Back along, Proff Frankel also wrote a much smaller book "Gravitational Curvature an Introduction to Einstein's Theory" : Freeman Publishing. Here he develops a lot of this, with and without tensors. He also notes and describes the several different fashions in the mathematical presentation of GR. These may be of interest.

Again thank you for your response. It is most interesting that you think to know all about my version of layers (especially when I haven't yet posted them) but fail to answer when I point out a contrdiction in the implementation of yours.

Thank you for this and your previous reply. However I was really looking for specifics wbout your system we could discuss but you made no refernce to it. As to my chinese problem, I was suggesting running the solution in your layer logic scenario and what I understand by layers for comparison purposes. But you have not doen this you you now assert that your method cannot solve those three simultaneous equations? Note the chinese wrapped the problem up in many words; I have just posted the core math of it in modern algebra.

Leading up to Marcus' comment I have marked the relevant result on the third page. @rjbeery I don't know how deeply you want to go but this is a simple derivation with one static source of gravitational potential. Your theory must predict/reproduce what happens with multiple sources. I don't know if anyone has considered time dilation at lagrange points and lines where there are at least two such potentials.

I'm not sure it's 'layer' relevant but it's a good point. +1

Thank you for your replies. Unfortunately although they have shed some light, they leave me more puzzled than ever. Both the quoted examples assert ( in different ways) the independence of one 'layer' from another. So how is it possible to establish the 'truth value' of any succeeding or preceeding layer, given the truth value in a particular layer. This must be so since with your simple example of the truth value of any layer immediately succeeding the given one must be opposite to the given value. So there must be more to it than this Since you like quoting Chinese philosophers, here is a problem that is solved in 12 'layers' posed sometime between 200 BC and 10 AD in the Ancient Chinese test "Nine Chapters on the Art of Calculation" In modern parlance it is 3x + 2y +z = 39 5y + z = 24 4y + 8 z = 39 Perhaps you would like to look at it from the points of view of your layers and my 12 layers, for comparison?

Thank you for the response. I did not say they were the same but I did (and still do) see some common features. I was really trying to establish some point to your 'layer logic' as I cannot see a 'whole' to understand and appreciate. There is a very clear reason for the 'layer model' and subsequent benefit from it, as exemplified in computing but which appears in many guises in most technical subjects. If you don't wish to discuss that further, that's fine by me. I will leave you to your musing.

Well I understood that rather impressive explanation. +1 Only one cooment. Marcus is talking 'field' in the mathematical sense, not the Physical sense. They can be slightly different.

Well in that case I will bow out and not bother further.

I do wish you would read my short comments properly. Especially as I have collected the bits together for you. You are clearly not following the (simple) point I am making. You have not one referred to the Raman effect, have you not come across it? Meanwhile others are pushing for mathematics. Here is some mathematics connecting refractive index, permittivity and permeability, including for the vacuum. https://www.doitpoms.ac.uk/tlplib/dielectrics/dielectric_refractive_index.php

The point is that in any physically substantial environment whatsoever ( I daren't say medium though that is the usual phrase) the transmission of light leads to two beams or rays. The main beam passes through, diminishing according to the Beer Lambert or similar law. Spectrophotometers mainly use this beam. The scattered ray, off at some angle, is the basis of Raman spectroscopy, which is also used in chemical analysis. Scattering is definitely something to think about, but it occurs when there's an abrupt change in media with an associated change in refractive index. We're considering a smooth, continuous gradation so I'm not sure how optics would normally handle that. Also, the Einstein Lens apparently doesn't differentiate by wavelength so perhaps spacetime neither disperses nor scatters as a "medium". I do appreciate the input, so thank-you. There is no change in media, abrupt or otherwise, in a chemical sample in a spectrophotometer.

The point is that in any physically substantial environment whatsoever ( I daren't say medium though that is the usual phrase) the transmission of light leads to two beams or rays. The main beam passes through, diminishing according to the Beer Lambert or similar law. Spectrophotometers mainly use this beam. The scattered ray, off at some angle, is the basis of Raman spectroscopy, which is also used in chemical analysis.

I would just like to point out here that Einstein did not refer to photon's or quantum theory when he introduced relativity and light clocks. Indeed he carefully avoided the mechanism of light until he had included it in his maths where he always discussed a light pulse. The light pulse being the instantaneous 'front' of whatever constitutes a travelling light ray. 'Das lichtquant' was another paper, directed at and confined to other effects.