rjbeery

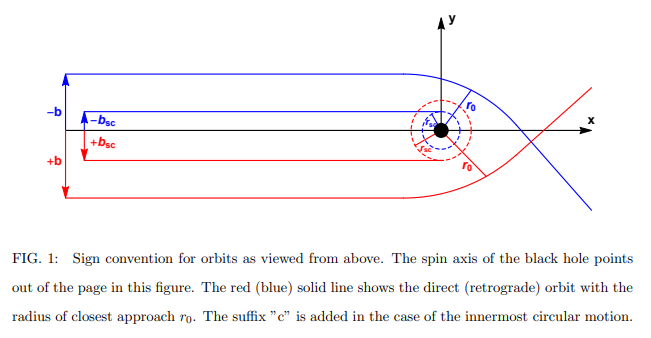
I think the crux of the light trajectory around a Kerr-Newman black hole is showcased in this diagram. If geodesics were to be strictly determined by time dilation this would imply that the field gradient is no longer strictly radial, but rather manifests as a spiral. Would you agree that this is possible, in theory? I'll investigate.

I acknowledge your point and appreciate your input very much. You'll forgive me if I remain skeptical. I need to find a scenario where the time dilation gradient cannot be used to determine the geodesic, and I don't think spinning mass qualifies. If light rays were to curve differently depending upon whether the mass was approached "with or against" the direction of spin then I do think that I would need to concede your point completely. Let me think about it some more.

But in the frame-dragging scenario you provided the geodesics of light rays are identical regardless of direction around the rotating mass. The reference clock is the Schwarszchild coordinate time of the infinite observer. I feel like you think my essay is trying to replace GR, but it's literally relying on GR to calculate time dilation and then using the gradient of that to determine geodesics. Geodesics alone to not describe everything about spacetime. Place observer A inside a massive, transparent, hollow sphere, and observer B "at infinity" (with coordinate time). They will each claim to be inertial, with no local gravitational effects. Physics for both observers is identical because their local time dilation gradient is zero, even though the time dilation of observer A is higher than that of B.

The path of the light ray is determined by the gradient of the scalar time dilation field. It’s a vector. Frame dragging apparently does not affect the radial gradient of time dilation. Note that this if not the same thing as not affecting the time dilation field itself.

It isn't a single quantity, it's a scalar gradient. I'm not exactly sure what you're asking here, but frame-dragging is my response. Anyway, as I said, different time dilation effects do not necessitate a change in direction. The straw will continue to appear to move "straight down" into a fluid, regardless of any change in index of refraction, because the surface of the fluid is perpendicular to the movement of the straw.

I understand now. Yes, you are correct, time dilation (on its own) does not effect a light ray's path because it is the gradient that determines curvature. Even in an accelerated frame, where time dilation would exhibit a gradient, that gradient is in the direction of travel -- so, again, no curvature. We see the same thing when we stick our straw straight-down into the water; the index of refraction changes, but the path of light does not.

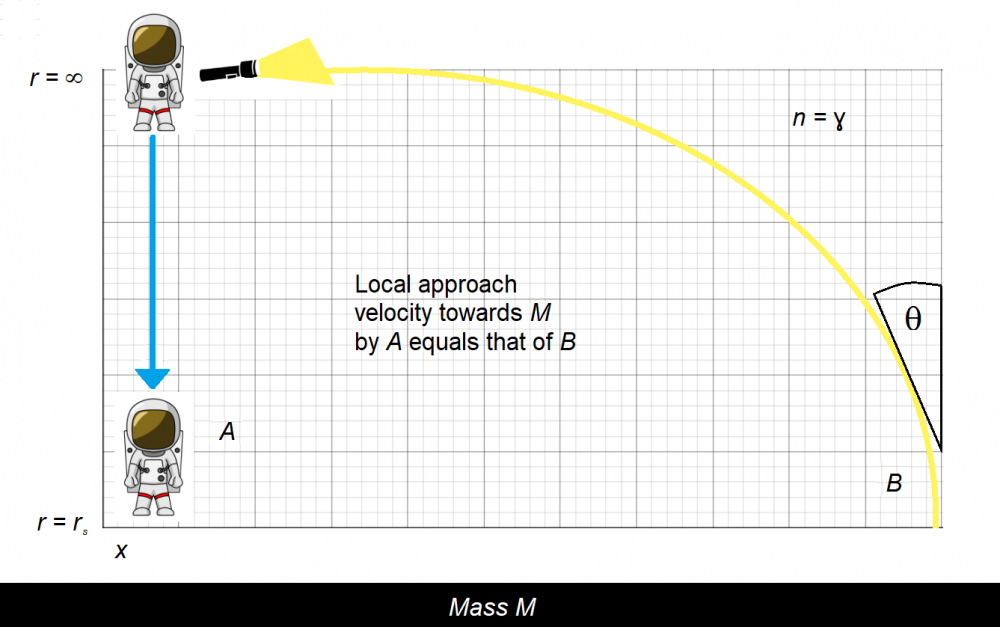
The speed of light is taken to be invariant locally. If time is slowed down by 50% "over there" then the speed of light has also been slowed down "over there". I'm sorry but I looked at all of your posts following my initial essay post, and I'm not sure which scenario you're referring to. Yes. Have you looked at the diagram? Gamma is 1 at r = infinity. There is no bending of light in deep space; there is no gravity in deep space; there is no time dilation in deep space. I think perhaps you're mistakenly thinking about the meaning of gamma.

\frac{num}{denom} $\frac{1}{3}$ [tex]\frac{1}{3} good? \begin{document} \frac{1}{3}

I have a full response, but I cannot get LATEX to work. Here's the short, ugly version: t_0 * gamma = t_r where gamma >=1, t_0 is the remote observer, and t_r is a clock at radius r above a large mass. For every second of t_r, the remote observer sees "t_0 * gamma" seconds pass on his local clock. Now we take c_0 as the local (relative to the remote observer) velocity of light, and c_r as the velocity that the remote observer measures at radius r above the large mass. Velocity has time on the denominator, so we have c_0 / gamma = c_r where a local light-ray moves one light-second per second, but that same light-ray moves "one over gamma light-seconds per second" at radius r. This should make intuitive sense. If gamma = 2, then the clock at r moves half as fast; therefore light moves half as fast. This gives gamma = c_0 / c_r which is the velocity of light "in a vacuum" over the velocity of light in another medium, which is the precise definition of the index of refraction.

The light ray, B, isn't bending due to gravitational effects; it's bending due to the refraction index being set to the time dilation function. See "n = gamma" in the corner? B is approaching the mass M purely through optical considerations. I gave this some thought. My response is that the gravitational potential may be the same for each ray, and the time dilation may be different, but it's the gradient that determines the optical path of each. We'd need a scenario where light rays take similar paths but move through different radial gradients.

Gravitational potential isn't even at the heart of anything here. For the falling body, A, I'm using PE + KE = constant as a shortcut to determine the free-fall kinetic energy as a function of r. The shell velocity could be determined in other ways. As for the light ray, B, I never refer to gravitational potential at all. GR time dilation is what determines the geodesic. Surely you'll agree that the GR time dilation field, as determined by an observer, is in fact a differentiable field? I'm not refuting GR in any way. I'm showing a mathematical analogy between two disparate fields (gravity and optics) and suggesting that they are literally the same thing. This doesn't change any predictions made by GR, but it certainly could simplify mathematical treatments in it. I'm not sure why you would want to discuss a paper, or even raise objections to it, if you won't read it. That seems a bit combative to me. Nevertheless, the entire concept can be summarized in the following diagram.

Poorly worded. The change in the velocity of light is caused by a change in the index of refraction of the traversed medium. A slowing of light is the very definition of time dilation. Did you read my paper? Because you made a vague remark implying that you did not.

It's time dilation caused by a change in the velocity of electromagnetic waves as measured by the index of refraction. Whether that cause is due to an abrupt change in the medium of travel, like vacuum-to-water, or if it's due to a gradual change in the medium of travel, like space-time approaching a large mass, is irrelevant. The math and behavior, both theoretical and in practice, are equal in both scenarios...and the presence of gravitational potential is not required. In other words, the change in velocity is (apparently) necessary and surely sufficient to display gravitational behavior.

I'm not exactly sure what your objection is. If this is it, then we take a glass of water in deep space (i.e. constant gravitational potential of zero) and stick a straw in it; the straw will appear to bend, and it's due to a reduction in the velocity of light in water.

Why do you say this? Why would gravitational potential require those boundary conditions? Off-the-cuff, I would say that movement in a direction opposite of a rotating body increases the corresponding relativistic masses of the respective objects. Increased time dilation should be expected. I believe what you're submitting is that, even if the potential/refraction connection is correct, that gravitational potential cannot accurately describe expected gravitational movement in GR. Is that right?