studiot

Fixed.

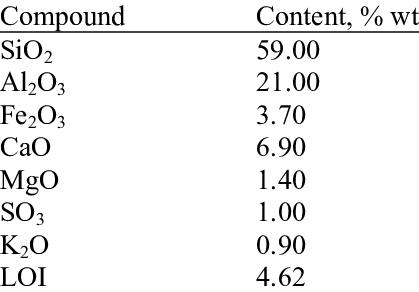
I asked you a simple question to which you have not made any reply. All you have done is repeat your early claim more strongly without any support whatsoever. So I will make it eay for you. The waste material from coal burning is called PFA (pulverised fuel ash) or fly ash. Far from being worthless it is a useful industrial material in its own right as it is pozzolanic. To make it easy here is a breakdown of the minerals in PFA https://onlinelibrary.wiley.com/doi/abs/10.1002/jctb.2720240405 The reaction of calcium oxide and carbon dioxide. This will lock up some carbon dioxide, but will not make any progress towards turning the waste into arable soil.

Thank you for the information. The Wiki article you linked to seems to suggest fracturing would be needed.

@Ayub Umar Whilst I think you suggestion will do far more harm than good, it is really good that you are thinking about soil health. The continued reduction of soil health over large swathes of the planet is a hidden danger for us all. https://www.bbc.co.uk/news/business-63283986

The point is we want numbers not hand waving. If you go to your bank manager and say There are lots of cheap bananas and coconuts in the Windward Islands. I want to make money by buying them there, taking them to New York and selling them for much higher prices. He will say What is you business plan ? I want numbers. How much do they cost? how much can you sell (some) of them for? How much wastage and unsold stuff will you have? What are your storage and transports costs? What are you import regulatory costs? What are you staff costs? It's the same with Science and Technology. It's up to you to show the true maths, not offer wishy washy statements like

And I did ask for an example of this 'anything' , whilst at the same time pointing to a well respected treatment of QM, involving plenty of imaginary and/or complex numbers. But this is taking the discussion away from the key statement Yes I am aware of extension algebras and arithmetic and I know tha there are some pretty exotic creations floating around there, but I am not very adept at them. I was always given to understand that for every gain in one direction you tend to loose something in another when you add to algebraic complexity.

Entirely ? I don't think so. But then I don't think you mean quite that literally. Nor are real numbers entirely commutative either. For example multiplication and square rooting are not commutative 2.√3 is not equal to √2.3 They are both commutative for either of the two operations of addition and multiplication as befits their status as Fields, which I believe I mentioned. But QM commutation is about the commutation of two different operators. So can you detail your real operators in QM that do not commute ? The dreaded 'i' seems to appear lots in this treatment. https://quantummechanics.ucsd.edu/ph130a/130_notes/node109.html Maybe the factorisation was stretching things a bit far as composition is involved, but I can't see what you mean by this How is (1+√5)/2 an element of an integer ring, when division is not closed with the integers ?

Actually there is more to what Markus said than meets the eye. The twist in the tail of using complex numbers in QM lies in non cummutativity. The 'full' set of complex numbers entail numbers of the form a + bi, where a and b are real numbers. Both the real numbers and the complex numbers formed this way form an algebraic Field and enjoy all the field properties, including the 10 Field axioms. One of the most important consequences is the unique factorisation theorem which guarantees unique solutions to all alegbraic equations in one of these Fields. Now Gauss discovered and did a lot of work on something simpler, we now call 'Gaussian Integers'. These connect ordinary integers with Gaussian integers in the same way as the reals and the complex numbers. So if p and q are integers then p + qi are gaussian integers. Now neither the ordinary integers nor the gaussian integers form an algebraic Field. They only satisfy 6 of the field axioms. But they do form a more general algebraic structure called a Ring. Some rings such as the integers still satisfy unique factorisation so for instance the only factorisation of -28 is -(1x2x2x7). But in the ring p+q√5i, the number 6+0i factorises as follows:- (2+0i)x(3+0i) and also (1+√5i)(1+√5i) Such rings of complex numbers fail to satisfy unique factorisation - essentially a quantum behaviour.

That's exactly right, well done. +1 'Complex' means made of more than one part and as you say 'The Complex Numbers' are made of two parts. What did you think of the other information poeple provided ?

Thank you for your further reply. This is your thread and your proposal. Whilst it is interesting to discuss generalities, it is up to you to explain the chemistry of how it works, especially in the Chemistry section. But so far you have only offered generalities. If you injected carbon dioxide into any type of earth material, what chemistry would be involved to keep it there ? Why would it react at all rather than just dissipate ?

My apologies that equation should have been 20x2-2x+1=0.

If the armour plating on a tank or a battleship is insufficient shielding against an EMP weapon, I doubt you could shield you computer. It has been suggested that old fashioned valve technology is more resistant than modern semiconductors on account of the very much higher breakdown voltages/field strengths involved.

You have posted this in Applied Mathematics, and it is true that most if not all applications can be handled in other ways. Perhaps you do not know the role played by complex numbers in Pure Mathematics. Perhaps the simplest answer is that number systems were developed in sequence starting with the simplest counting numbers, Going through systems including The full set of integers. The ratioanl numbers (fractions) The real numbers The imaginary numbers The complex numbers (do you know the difference between imaginary numbers and complex numbers ? What does complex mean ? Now each of these systems was introduced when it bcame apparent that there were equations in the simpler system, that had no solutions in the simpler system. For instance the equation 2x = -30 has no solution in the counting numbers or the positive integers, the equation 2x = 1 has no solution in the integers, the equation 2x2-20x+1=0 has no real solutions - both solutions are complex. So complex numbers are necessary to provide solutions to all quadratic equatuions. Some equations of higher order do not even have a solurion formula withoug involving complex numbers. It is just fortunate happenstance that having developed complex numbers they find many useful applications elsewhere. Of course the process has not stopped there, there are even more complicated 'number' than complex ones.

I was going to put my reasoning for my statement into an answer in the 'movement without time thread' , but the OP there seems to have lost interest. So I will just point out that some (very important) equations of motion have time independent solutions.

Others have already commented on the unwanted chemical side effcts of your proposal. +1 each. So I will concentrate on asking how you would achieve your desired ones. How would the chemistry of 'infusing with carbon' work ? What would be the production rate of such a process and what would ecological transport costs of placing it somewhere useful ? Why would you need a greenhouse-like structure ? Why would an ordinary shed not do and how big would that shed be ? I would just like to add that Drax represents one of the biggest cover ups of wasted public money and effort in our history.

Surely this failure, by someone who clearly doesn't know what they are talking about, to provide proper Physics and Maths support in a mainstream forum has gone on long enough.

Is this some sort of project you are studying ? I do not think attempting statistical data comparisons is the right way to go about it. You need a model to discuss. Your model should identify major and minor factors of formation and inparticular classify where climate fits in. Yes climate is a factor in soil formation, but no by itself climate cannot indicate current soil type. That is because formation is historic and the climate may heve been different during that time. So you need to distinguish between historic climate and present day climate. I reckon climate to be a minot factor because no climate regime can create soil types that which do not derive from the parent geology. For example China Clay is a particular 'soil' and is derived from the weathering of a partuclar form of Granite. If the underlying rocks ar not made of this granite, they cannot weather to china clay, whatever the climate. I recommend obtaining, reading and using as a eference, World Soils by E M Bridges of the International Soil Reference and Information Centre, Wageningen Cambridge University Press It offers suitable models etc for your project.

How do you know this ?

But his statement is just not true. I prefer "Time and Tide wait for no Man" At one time the truss was the only solution. Inguinial hernias are by far and away the most common, with the patient's right hand side accounting for over 90% of cases. I had one done in 2016, a repair that has remained successful since then. I was also one of the unlucky ones who developed a LHS one in 2021 and had that repaired just before Christmas, at the ehight of the December Covid wave. Again an excellent job. Both time were done at a clinic that is a shining example of state - private working together in close harmony, demonstrating that thre is no intrinsic reason for such practice to work well.

Can you reference any superconducting tubes that don't require energy input to maintain the superconducting state ?

Well you should care. Heat capacity is the capacity to absorb heat, yes. But once absorbed you want to store it and finally retrieve it, not loose it or waste it. This is where heat conduction and heat transfer coefficients become important. Thermodynamics forces you to store heat energy at a higher temperature than the surroundings you want to keep warm. Note this is different from chemical, mechanical potential or electrical energy. But you want to release it gradually as slowly as needed otherwise much goes to waste. The design of electric night storage radiators has greatly improved over the years as manufacturers slowly recognised this very important factor. Seth's cast iron Rayburn was a classic victorian implementation of this knowledge as were the massive cast iron fireplace surrounds they used to install. +1

Not sure where to put this so I am starting with other science if we can include bonkers maths as currently practiced by UK politicians. I have recently received notification from my electricity supplier company that my standard tariff has increased from £0.2992 per kW-hr to £0.3661 per kW-hr. So imagine my suprise to see this report by the BBC. https://www.bbc.co.uk/news/business-63329233 What ?????????? they will pay me £3.00 to use off peak electricity ? When do I get started, I plan to use as much as possible. Will I get rich quick ?

I suggest the following strategy. Start at the beginning and attempt maths questions from that year's material, from any source that you can get hold of so long as the answers are also provided. You don't need to achieve grades or marks, just to find out what you know and what you don't know. Hopefully, as you say, it will come easy at this stage and you will fly through the material. Quickly review wrong answers and check the teaching material for that topic if you get several wrong on a particular thing. Eventually you will find questions you can't answer. This is where you stop, go back and study the teaching material for that year, going forward at your own pace. Make sure you try the questions again and even if you don't get them all right, make sure you understand how to do them. Finally you will decide that you are no longer just filling in gaps but need to take your studies forward from where you left off a few years ago.

I hate to tell you this but it is just about impossible to learn any technical subject topic by topic. This is particularly true for Mathematics. The reason for this is that all the topics are inter-related. You need to know a little bit of arithmetics to study algebra and a little bit of algebra to study geometry, but also a little bit of geometry at the beginning of algebra and so on. That is why the the same topics are revisited at every grade, but at a higher level.

If Rees-Mogg backs it then it must be right. After all he is the barrister who backed the ex chancellor and tottering prime minister. So he is clearly a nuclear physics expert. As a matter of record the UKAEA has already attempted to build a fusion reactor at least twice and failed to make it work.