Orion1

Are there any detectable theoretical deviations from the mathematical solutions already published by mainstream science? Any discussions and/or peer reviews about this specific topic thread? "You will do well to expand your horizons." - Fortune Cookie

Besides the Interior Schwarzschild metric, has any of these other interior solutions been published by scientists? [math]\text{Interior Schwarzschild metric:} \; (J = 0,Q = 0) \; \; \; (\text{ref. 1})[/math] [math]\text{Interior Reissner-Nordstrom metric:} \; (J = 0,Q \neq 0)[/math] [math]\text{Interior Kerr metric:} \; (J \neq 0,Q = 0)[/math] [math]\text{Interior Kerr-Newman metric:} \; (J \neq 0,Q \neq 0)[/math] Would you interested in preserving these published interior solutions in your academic library archive to survive the author's and server's longevity and for the future study of these interior solutions by students or professors? Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Interior Schwarzschild metric: (ref. 1) https://en.wikipedia.org/wiki/Interior_Schwarzschild_metric#Mathematics

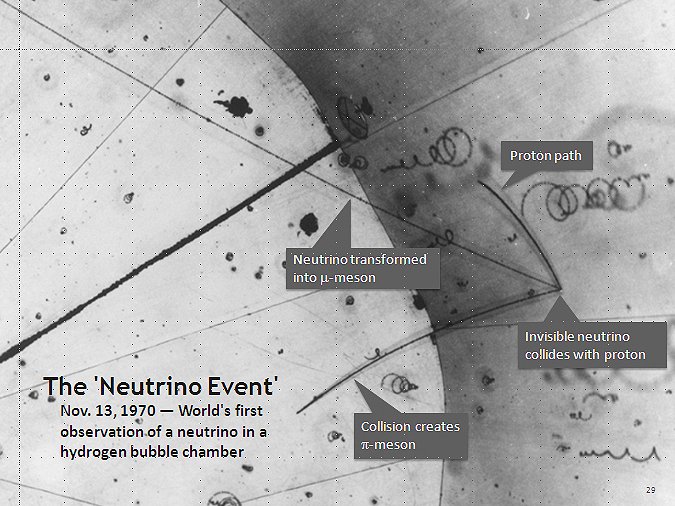
This file has been identified as being free of known restrictions under copyright law, including all related and neighboring rights. "The first use of a hydrogen bubble chamber to detect neutrinos, on 13 November 1970, at Argonne National Laboratory. Here a neutrino hits a proton in a hydrogen atom; the collision occurs at the point where three tracks emanate on the right of the photograph." (ref.1) The neutrino track itself is invisible in a bubble chamber due to the neutrino having zero charge and only interacts via the weak nuclear force. However the neutrino path can be deduced by the resultant particle production angles. Coherent neutrino scattering has been seen with a compact detector. (ref. 2) In my opinion, two or more of these coherent neutrino detectors would be capable of determining if neutrinos scatter through zero-mass Compton scattering or through a non-zero-mass process that is described by the equations above and capable of determining the neutrino rest-mass with a high degree of precision. This is the correct intuitive answer, although any modern physics textbook would be challenged to provide such a comprehensive answer, beyond a photon scattering process. Reference: Wikipedia - Neutrino: (ref. 1) https://en.wikipedia.org/wiki/Neutrino Physicsworld - Coherent neutrino scattering: (ref. 2) https://physicsworld.com/a/coherent-neutrino-scattering-seen-with-compact-detector/

If a neutrino has zero mass, would the neutrino obey Compton scattering? Any modern physics textbook answers this question for zero mass photons, however, do they also answer for zero mass neutrinos? Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Compton scattering - Derivation of the scattering formula: https://en.wikipedia.org/wiki/Compton_scattering#Derivation_of_the_scattering_formula

Arizona House Bill 2319 ruled unconstitutional. A federal judge has ruled that an Arizona law limiting how close people can get to recording law enforcement is unconstitutional, citing infringement against a clearly established constitutional Right of the public to film the official activities of police officers in a public place. (ref. 1) Arizona House Bill 2319 was struck down as unconstitutional primarily because it violated the Supremacy Clause, which constitutionally protects Rights such as Freedom of the Press, and protects against Prior Restraint, and which constitutionally granted a federal circuit judge the authority to strike down the law as unconstitutional. Arizona House Bill 2319 is also an unconstitutional form of Prior Restraint, and there is an established constitutional Right of the public to film the official activities of police officers in a public place, which is a constitutionally protected First Amendment form of Freedom of the Press. The Supremacy Clause is the provision in Article 6, Clause 2 of the United States Constitution that establishes the Constitution, AS THE SUPREME LAW OF THE LAND. No state can make a higher law and if it tried no judge could enforce any such law. That law would become a legal fiction, as if it never existed. Article 6, Clause 2 of the United States Constitution: This [United States] Constitution, and the Laws of the United States which shall be made in Pursuance thereof; and all Treaties made, or which shall be made, under the Authority of the United States, shall be the supreme Law of the Land; and the Judges in every State shall be bound thereby, any thing in the Constitution or Laws of any State to the Contrary notwithstanding. "The Constitution of these United States is the supreme law of the land. Any law that is repugnant to the Constitution is null and void of law." "void ab initio" - Marbury v. Madison, (5 US 137) "Where Rights secured by the Constitution are involved, there can be no 'rule making' or legislation which would abrogate them." - Miranda v. Arizona, (384 U.S. 426, 491; 86 S. Ct. 1603) "An unconstitutional act is not law; it confers no Rights; it imposes no duties; affords no protection; it creates no office; it is in legal contemplation, as inoperative as though it had never been passed." - Norton v. Shelby County, (118 U.S. 425 p. 442) Ninth Circuit (with jurisdiction over Alaska, Arizona, California, Guam, Hawaii, Idaho, Montana, Nevada, the Northern Mariana Islands, Oregon, and Washington). "material fact exists concerning whether [Police] interfered with Fordyce's First Amendment Right to gather news." - Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995); "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013); "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii Any discussions and/or peer reviews about this specific topic thread? Reference: ACLU - Arizona House Bill 2319: (ref. 1) https://www.acluaz.org/en/press-releases/federal-court-blocks-unconstitutional-police-recording-bill-aclu-arizona-reacts Wikipedia - Supremacy Clause: https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Prior Restraint: https://en.wikipedia.org/wiki/Prior_restraint

"Why don't you tell us?" - swansont "What is the question, exactly?" - Markus Hanke Are there any detectable theoretical deviations from the mathematical solutions already published by mainstream science? It is noted that these exterior solutions are pure mathematical 'artifacts' of General Relativity for a universe with asymptotic flatness. A constructive critique response under a peer review would have been preferred to potentially highlight any other detectable theoretical deviations, and I always try to provide such an opportunity for students and professors. This type of academic strategy has proven to be more effective for improved research quality than mere dictate. The only detectable deviation from this theory is the theoretical discontinuity with the cited temporal Kerr metric tensor element, which fails to reduce into an ellipsoid when a massless parameter state is directly mathematically applied. However, the cited temporal Kerr metric tensor element published by Kerr is a mathematical identity with the temporal Kerr metric tensor element generated by this theory. Would any students or professors be interested in preserving these published exterior solutions in their academic library archive to survive the author's and server's longevity and for the future study of these exterior solutions by students or professors? Any discussions and/or peer reviews about this specific topic thread? "You will do well to expand your horizons." - Fortune Cookie

"None of the metrics in the Kerr-Newman family will realistically appear in the real world in an exact way, because all four of them require asymptotic flatness - meaning these require an otherwise completely empty universe. A more realistic - yet still idealized - family of solutions would be the Vaidya spacetimes." - Markus Hanke It is noted that these interior solutions are pure mathematical 'artifacts' of General Relativity for a universe with asymptotic flatness. Besides the Interior Schwarzschild metric, has any of these other interior solutions been published by scientists? [math]\text{Interior Schwarzschild metric:} \; (J = 0,Q = 0) \; \; \; (\text{ref. 1})[/math] [math]\text{Interior Reissner-Nordstrom metric:} \; (J = 0,Q \neq 0)[/math] [math]\text{Interior Kerr metric:} \; (J \neq 0,Q = 0)[/math] [math]\text{Interior Kerr-Newman metric:} \; (J \neq 0,Q \neq 0)[/math] Would any students or professors be interested in preserving these published interior solutions in their academic library archive to survive the author's and server's longevity and for the future study of these interior solutions by students or professors? Any discussions and/or peer reviews about this specific topic thread? "You will do well to expand your horizons." - Fortune Cookie Reference: Wikipedia - Interior Schwarzschild metric: (ref. 1) https://en.wikipedia.org/wiki/Interior_Schwarzschild_metric#Mathematics

In political science, the burden of proof is on the individual making the claim. Please cite a case law "decision" that is relevant to this discussion. As was already cited, the State and Federal constitutional levels have made many corrections. As of 2014, the United States Supreme Court has held 176 Acts of the U.S. Congress unconstitutional. In the period 1960–2019, the Supreme Court has held 483 laws unconstitutional in whole or in part. (ref. 2) As of 2017, the United States Supreme Court had held unconstitutional portions or the entirety of some 182 Acts of the U.S. Congress. (ref. 3) As of 2017, the United States Supreme Court had held unconstitutional portions or the entirety of some 238 State constitutional, statutory provisions and municipal ordinances. (ref. 4) As of 2018, the Supreme Court had overruled more than 300 of its own cases. (ref. 5) "This Constitution, and the Laws of the United States which shall be made in Pursuance thereof; and all Treaties made, or which shall be made, under the Authority of the United States, shall be the supreme Law of the Land" - The Supremacy Clause, Article VI, United States Constitution. (ref. 1, ref. 2) "all Treaties" includes Peace Treaties. ☮️🕊️ What is written in the Federal Constitution IS the Unites States Constitution. We are educated and civilized statesmen and scientists, and we do not condone violence against anyone. ☮️🕊️ Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Supremacy Clause: (ref. 1) https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Judicial review in the United States: (ref. 2) https://en.wikipedia.org/wiki/Judicial_review_in_the_United_States Wikipedia - Judicial review in the United States: (ref. 3) https://en.wikipedia.org/wiki/Judicial_review_in_the_United_States#Judicial_review_after_Marbury GovInfo - State Constitutional And Statutory Provisions And Municipal Ordinances Held Unconstitutional (ref. 4) https://www.govinfo.gov/content/pkg/GPO-CONAN-2017/pdf/GPO-CONAN-2017-12.pdf Wikipedia - List of overruled United States Supreme Court decisions: (ref. 5) https://en.wikipedia.org/wiki/List_of_overruled_United_States_Supreme_Court_decisions

"The judicial power of the United States, shall be vested in one Supreme Court, and in such inferior [Federal] courts as the Congress may from time to time ordain and establish. ... The judicial power shall extend to all cases, in law and equity, arising under this [Federal] Constitution, the laws of the United States, and treaties made, or which shall be made, under their authority." - Article III, United States Constitution. (ref. 1) "This Constitution, and the Laws of the United States which shall be made in Pursuance thereof; and all Treaties made, or which shall be made, under the Authority of the United States, shall be the supreme Law of the Land; and the Judges in every State shall be bound thereby, any Thing in the Constitution or Laws of any State to the Contrary notwithstanding. ... [A]ll executive and judicial Officers, both of the United States and of the several States, shall be bound by Oath or Affirmation, to support this [Federal] Constitution." - The Supremacy Clause, Article VI, United States Constitution. (ref. 1, ref. 2) "No State in this union [United States] can alter or abridge, in a single point, the Federal articles [Federal Constitution] or the treaty." - Rutgers v. Waddington (1784) (ref. 1, ref. 3) "The supremacy of the legislature need not be called into question; if they think fit positively to enact a law, there is no power which can control them. When the main object of such a law is clearly expressed, and the intention manifest, the judges are not at liberty, although it appears to them to be unreasonable, to reject it; for this were to set the judicial above the legislative, which would be subversive of all government." - Rutgers v. Waddington (1784) (ref. 1, ref. 3) The defense's case was litigated by Alexander Hamilton, who posited that the [State] Trespass Act violated the [Federal] 1783 peace treaty, which had been ratified by the [Federal] United States Congress. Alexander Hamilton decided that the case would be a good test of ruling the legality of the [State] Trespass Act. (ref. 3) The original contention was that only Federal courts could rule laws unconstitutional [within their constitutional jurisdiction]. "unconstitutional" is an intrinsic generic de jure terminology to both the State and Federal level with respect to the State and Federal level constitutional jurisdictions, although it is typically implied to be Federal level jurisdiction, such an ambiguous assumption is not an absolute due to the de facto capability of both the State and Federal courts ruling laws unconstitutional [within their constitutional jurisdiction]. My statement was not inaccurate, in fact it was repeated verbatim, it only lacked a more descriptive definitive resolution of State and Federal jurisdictions, which appears to have been clarified. I would prefer that any proponent for liberty, not be subjected to a government censorship prior restraint law, and sentenced anywhere from 30 days to 15 years in prison, simply for advocating for free speech and press. Let us try our best to appeal these proponents' convictions. Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Judicial review in the United States: (ref. 1) https://en.wikipedia.org/wiki/Judicial_review_in_the_United_States Wikipedia - Supremacy Clause: (ref. 2) https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Rutgers v. Waddington (1784): (ref. 3) https://en.wikipedia.org/wiki/Rutgers_v._Waddington

In the United States, any local, State, or Federal judge can rule any law as unconstitutional, within their individual State or Federal constitution jurisdictions. A State judge can only rule a State law as unconstitutional within the State jurisdiction and State boundaries of the State Constitution. A Federal judge can rule both a State or Federal law as unconstitutional within the State or Federal boundaries of the Federal jurisdiction of the Federal Constitution under the Supremacy Clause. (ref. 1) The United States Supreme Court has never invalidated a State or Federal constitutional amendment on the grounds that it was outside the constitutional amending power. However, under the Supremacy Clause of the United States Constitution, if a State constitutional amendment conflicts with the Supremacy Clause of the Federal constitution, a Federal judge can rule that State amendment as unconstitutional within the Federal constitution jurisdiction. The State and Federal courts have both decided that under the Supremacy Clause of the United States Constitution, Federal law is superior to State law, and that under Article III of the United States Constitution, the Federal judiciary has the final power to interpret the United States Constitution. Therefore, the power to make final decisions about the constitutionality of Federal laws lies with the Federal courts, not the States, and the States do not have the power to nullify Federal laws. The Supremacy Clause of the Constitution of the United States (Article VI, Clause 2), establishes that the United States Constitution, Federal laws made pursuant to it, and treaties made under its authority, constitute the "Supreme Law of the Land", and thus take priority over any conflicting State laws. Only if a Federal courtroom jury decides to support such an inhumane partisan legality campaign. (ref. 2) Reference: Wikipedia - Supremacy Clause: (ref. 1) https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Jury nullification: (ref. 2) https://en.wikipedia.org/wiki/Jury_nullification_in_the_United_States

The ubiquitous proliferation of electronic devices with video-recording capability is insufficient to suspend already existent and established Civil and Constitutional Rights protected under the Supremacy Clause in Article 6, Clause 2 of the Unites States Constitution. In the United States, once a Constitutional Right has been established by a Federal Circuit Court, a State legislature cannot override, overrule, repeal, delineate, or detract from an already existent Federal Circuit Court ruling protecting an already established Constitutional Right, as that would be an unconstitutional violation of the Supremacy Clause in Article 6, Clause 2 of the United States Constitution. If a police officer is in fact "dealing with a suspect" while conducting "crowd control" duties, then there is a high degree of probability with the ubiquitous proliferation of electronic devices with video-recording capabilities, that many individuals, would be capable of recording and actively recording the conduct of such a police officer in public within a 15 feet distance inside a crowd. Such recording by individuals in a crowd for publishing on social media happens many times during street level protesting. The mass arrests of such journalists and mass confiscations of "ubiquitous prolific electronic recording devices" in public would be illegal under Federal laws and unconstitutional. This de jure case law 'Adkins v. Limtiaco (9th Cir. 2013)' is relevant to the the legislation, because it is one of the Federal 9th Circuit Court rulings that established video-recording police officers in public as a constitutionally protected activity under the constitutional Doctrine of Prior Restraint, that is protected by the First Amendment and the Supremacy Clause in Article 6, Clause 2 of the United States Constitution. This de jure case law is not only about police officers attempting to destroy Federal evidence, it is also about the violation of the First, Fourth, and Fourteenth Amendment Rights of an individual. "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 1, ref. 2) What is to guarantee that under such an "interference" law, the mass arrests of such journalists and mass confiscations of "ubiquitous prolific electronic recording devices" by police officers because of unconstitutionally broad and vague subjective "interference", and potentially subjected to abuse of authority, would not result in the mass destruction of Federal evidence where police officer Civil Rights violations allegedly occurred or police officer misconduct could allegedly be construed, or the innocence of a subject ascertained? Even with technology that is ubiquitously prolific, such as home and business security cameras, public street cameras, cell phone cameras, etc., and all within a 15 feet distance, there is no possible legal argument that would absolutely convince a State or Federal courtroom jury that such security systems constitute "interference" of police officer duties. A prior restraint is an official government restriction of free speech, journalism and press prior to publication. Prior restraints are viewed by the United States Supreme Court as "the most serious and the least tolerable infringement on First Amendment Rights" - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 2, ref. 3) Any discussions and/or peer reviews about this specific topic thread? Reference: Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013): (ref. 1) https://www.govinfo.gov/content/pkg/USCOURTS-gud-1_09-cv-00029/pdf/USCOURTS-gud-1_09-cv-00029-2.pdf Wikipedia - Prior restraint: (ref. 2) https://en.wikipedia.org/wiki/Prior_restraint Justia - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 3) https://supreme.justia.com/cases/federal/us/427/539/

...

If this legal argument was derived from reasonable deduction, then the derivative of the argument is because changes in technology was not yet sophisticated and consolidated to the point of practical portability for many people to use. However, there were hand held photographic cameras and microphone recording devices present at that time, they were simply not practical to use, unless someone was a specialized photographer, journalist or press. Had either or both of such impractical electronic devices been used in Adkins v. Limtiaco (2013), in which the Plaintiff also used a ubiquitous cell phone, which was also not ignored by the Federal Ninth Circuit Court, and based upon the de facto events which occurred, there is no doubt that the police officers would have responded with demands to destroy the photographic film and/or destroy the microphone recording. Or if a conventional "Channel Five News" news crew arrived on scene with a news reporter and a cameraman with the large, bulky shoulder mounted camera, which is still used at present time by press, only with increased electronic sophistication, the police officers would have responded with a prior restraint demand also: "When Plaintiff stopped his car, the [police] officer ("Officer One") told him that he could not take pictures." "[Police] Officer One spoke with a second police officer ("Officer Two") who was present, and then demanded that the Plaintiff give him the cell phone." "Officer Two then approached Plaintiff’s car and also demanded the cell phone." (now within a 15 feet distance) "Plaintiff said something like: "There’s no law against taking pictures."" "Officer Two again demanded the cell phone" "At that point, either Officer One or Officer Two grabbed Plaintiff’s cell phone and took it away." (First, Fourth, Fourteenth Amendment Violation) "When Plaintiff’s lawyer, [Redacted], arrived, a police sergeant demanded that [Plaintiff’s lawyer] delete the photos stored on Plaintiff’s cell phone. "[Plaintiff’s lawyer] refused." "The police sergeant then held out Plaintiff’s cell phone and demanded that he delete the pictures from it." "Plaintiff refused." "the Office of the Attorney General ("OAG") issued a "Prosecution Decline Memorandum" ("the Memorandum"), in which it explained that it would not prosecute Plaintiff on the charge for which he was arrested." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 1) "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 1, ref. 2) Police officers seizing a cell phone without a warrant is a violation of the First, Fourth, and Fourteenth Amendments to the United States Constitution. United States Supreme Court - Carpenter v. United States, No. 16-402, 585 U.S. (2018): (ref. 3) The demands by the police officers to destroy Federal evidence, is also a violation of Title 18 Code 241, 242, 1519 and 1911. The unlawful destruction of Federal evidence on a Federal evidence recording device by police officers is a violation of Title 18 U.S. Code § 1519 and Title 42 U.S. Code § 2000aa and other State and Federal laws and precedents. Title 18 U.S. Code § 241 - Conspiracy against Rights Title 18 U.S. Code § 242 - Deprivation of Rights under Color of Law Title 18 Code § 1519, Title 42 U.S. Code § 2000aa - Conspiracy to destroy Federal evidence by police officers Title 18 Code § 1911 - Police officer violations of oath of office. - Quern v. Jordan 440, U.S. 332, 345 (1979) Which warrants at minimum a Pro Se Plaintiff action under Title 42 U.S. Code § 1983 - Civil action for Deprivation of Rights. "Changes in technology and society have made the lines between private citizen and journalist exceedingly difficult to draw. The proliferation of electronic devices with video-recording capability means that many of our images of current events come from bystanders with a ready cell phone or digital camera rather than a traditional film crew, and news stories are now just as likely to be broken by a blogger at their computer as a reporter at a major newspaper. Such developments make clear why the news-gathering protections of the First Amendment cannot turn on professional credentials or status." - Glik v. Cunniffe, 655 F. 3d 78 - Court of Appeals, (1st Cir. 2011) "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii. (ref. 4) The ubiquitous proliferation of electronic devices with video-recording capability is insufficient to detract from or suspend Civil and Constitutional Rights protected under Article 6, Clause 2 of the Unites States Constitution. The Plaintiff in Adkins v. Limtiaco (2013) (ref. 1) was using a cell phone, and the Federal witnesses in the George Floyd case United States v. Chauvin (2021) (ref. 5), also used cell phones within a 15 feet distance, which proved very valuable Federal video evidence to Federal Circuit Court Judges and the United States Department of Justice. It is also de facto that all police departments are not yet fully equipped with body cameras. (ref. 6) In November 2018, the Bureau of Justice Statistics published a report on the use of body-worn cameras by law enforcement agencies in the United States in 2016: Only forty-seven percent (47%) of general-purpose law enforcement agencies had acquired body-worn cameras, and for large police departments, that number is only eighty percent (80%). (ref. 6) The ubiquitous proliferation of cell phones, and the more cell phones recording police officers at different angles in the course of the police officers' duties, within a 15 feet distance, has already proven itself to serve a greater benefit to Justice for We The People, than to its detriment. Even if the technology is ubiquitously prolific, such as home and business security cameras, public street cameras, cell phone cameras, etc., and all within a 15 feet distance, simply filming police officers in the course of the police officers' duties is not interference. In terms of protecting the police officers, if someone is standing there holding a cell phone, it does not endanger the police officers in any way. "The record in this case includes a 'videotape' capturing the events in question." "...the 'record' blatantly contradicts the [subject's] version of events so that no reasonable jury could believe it, a court should not adopt that version of the facts for purposes of ruling on a summary judgment motion." - United States Supreme Court - Scott v. Harris, 550 U.S. 372 (2007) (ref. 7) Any discussions and/or peer reviews about this specific topic thread? Reference: Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013): (ref. 1) https://www.govinfo.gov/content/pkg/USCOURTS-gud-1_09-cv-00029/pdf/USCOURTS-gud-1_09-cv-00029-2.pdf Wikipedia - Prior restraint: (ref. 2) https://en.wikipedia.org/wiki/Prior_restraint United States Supreme Court - Carpenter v. United States, No. 16-402, 585 U.S. (2018): (ref. 3) https://www.supremecourt.gov/opinions/17pdf/16-402_h315.pdf Hawaii v. Russo (2017) - Supreme Court of Hawaii: (ref. 4) https://cases.justia.com/hawaii/supreme-court/2017-scwc-14-0000986-0.pdf United States Department of Justice - United States v. Chauvin - CASE 0:21-cr-00109-WMW-HB (2021): (ref. 5) https://www.justice.gov/opa/press-release/file/1392446/download United States National Institute For Justice - Research on Body-Worn Cameras and Law Enforcement: (ref. 6) https://nij.ojp.gov/topics/articles/research-body-worn-cameras-and-law-enforcement Justia - Scott v. Harris, 550 U.S. 372 (2007): (ref. 7) https://supreme.justia.com/cases/federal/us/550/372/

If this legal argument was derived from reasonable deduction, then this is the legal argument that should have been presented during the FIRST United States Federal Ninth Circuit Court case on this Civil Rights issue. In Fact, 'De Facto', the United States Federal Ninth Circuit Court ruled the exact opposite as 'De Jure' case law: "material fact exists concerning whether [Police] interfered with Fordyce's First Amendment Right to gather news." - Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995) (ref. 2) In Fact, 'De Facto', the United States Supreme Court also ruled the exact opposite, as prior restraint is "the most serious and the least tolerable infringement on First Amendment Rights" - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 3, ref. 4) In the United States, once a 'De Jure' Federal case law on Civil Rights protected by Article 6, Clause 2 of the United States Constitution has been established, a Federal Ninth Circuit Judge becomes bound within the parameters of that Federal Ninth Circuit Court decision, and cannot detract from such Federal judicial rulings, without severely undermining their constitutional judicial peer integrity and making an unconstitutional ruling that is capable of being overturned by the appellate and supreme courts. In this instance, a U.S. Citizens First Amendment Right to gather news in a public space without prior restraint interference. And since the Federal Ninth Circuit Court did not establish a magical fifteen feet (15') distance, no such de jure or de facto distance exists, and any State or Federal legislature and/or State or Federal court that detracts from such established Federal Ninth Circuit Court case law parameters, would in fact be conducting prior restraint themselves. "Where Rights secured by the Constitution are involved, there can be no 'rule making' or legislation which would abrogate them." - Miranda v. Arizona, (384 U.S. 426, 491; 86 S. Ct. 1603) "The Constitution of these United States is the supreme law of the land. Any law that is repugnant to the Constitution is null and void of law." "void ab initio" - Marbury v. Madison, (5 US 137) Ninth Circuit (with jurisdiction over Alaska, Arizona, California, Guam, Hawaii, Idaho, Montana, Nevada, the Northern Mariana Islands, Oregon, and Washington). The United States Federal Ninth Circuit Court: "material fact exists concerning whether [Police] interfered with Fordyce's First Amendment Right to gather news." - Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995) (ref. 2) "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 3) "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii. (ref. 4) Arizona House Bill 2319 is specifically enforcing unconstitutional prior restraint penalties for the First Amendment exercise of free speech, journalism and press prior to publication. A prior restraint is an official government restriction of free speech, journalism and press prior to publication. Prior restraints are viewed by the United States Supreme Court as "the most serious and the least tolerable infringement on First Amendment Rights" - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 5, ref. 6) If passed, Arizona House Bill 2319 is expected to be struck down as "unconstitutional" in the United States Federal Ninth Circuit Court within 3 years. Reference: House Bill 2319 - anyone who police order to stop filming but continues to do so would face a class 3 misdemeanor and up to 30 days in jail: (ref. 1) https://www.azleg.gov/legtext/55leg/2R/bills/HB2319P.pdf Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995): (ref. 2) https://caselaw.findlaw.com/us-9th-circuit/1054985.html Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013): (ref. 3) https://www.govinfo.gov/content/pkg/USCOURTS-gud-1_09-cv-00029/pdf/USCOURTS-gud-1_09-cv-00029-2.pdf Hawaii v. Russo (2017) - Supreme Court of Hawaii: (ref. 4) https://cases.justia.com/hawaii/supreme-court/2017-scwc-14-0000986-0.pdf Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) - United States Supreme Court (ref. 5) https://tile.loc.gov/storage-services/service/ll/usrep/usrep427/usrep427539/usrep427539.pdf Wikipedia - Prior restraint: (ref. 6) https://en.wikipedia.org/wiki/Prior_restraint

Any discussions and/or peer reviews about this specific topic thread? "I think of the horizon at midnight, the sky and sea blurring together." - Sophie Hardcastle Reference: Wikipedia - Schwarzschild metric - Flamm's paraboloid: (ref. 1) https://en.wikipedia.org/wiki/Schwarzschild_metric#Flamm's_paraboloid Wikipedia - Schwarzschild radius: (ref. 2) https://en.wikipedia.org/wiki/Schwarzschild_radius Wikipedia - Schwarzschild metric: (ref. 3) https://en.wikipedia.org/wiki/Schwarzschild_metric Wikipedia - Boyer-Lindquist coordinates - Line element: (ref. 4) https://en.wikipedia.org/wiki/Boyer-Lindquist_coordinates#Line_element Science Forums - General Relativity: Four Exterior Metric Solutions - Orion1: (ref. 5) https://www.scienceforums.net/topic/126549-general-relativity-four-exterior-metric-solutions/ Wikipedia - Photon sphere: (ref. 6) https://en.wikipedia.org/wiki/Photon_sphere Wikipedia - Astrophysical jet: (ref. 7) https://en.wikipedia.org/wiki/Astrophysical_jet Wikipedia - Accretion disk: (ref. 8) https://en.wikipedia.org/wiki/Accretion_disk Wikipedia - Black hole - Innermost stable circular orbit: (ref. 9) https://en.wikipedia.org/wiki/Black_hole#Innermost_stable_circular_orbit_(ISCO) Mathematica 7 - General Relativity - Flamm's Paraboloid source code notebook attachment: General Relativity - Flamm's Paraboloid.nb Mathematica 7 - General Relativity - Schwarzschild Black Hole Toy Model source code notebook attachment: General Relativity - Schwarzschild Black Hole Toy Model.nb Please merge the threads if there is a protocol violation.