Orion1

In Einstein's theory of General Relativity, the exterior metric or exterior metric solution, is an exact solution to the Einstein field equations and Einstein-Maxwell equations that describes the metric space-time geometry in the exterior of a non-rotating or rotating neutral or charged spherically symmetric metric, and that the electric charge and angular momentum of the metric may be zero or non-zero, and the universal cosmological constant is zero. For a non-zero charged metric, the metric takes into account the Einstein-Maxwell field energy of an electromagnetic field within the space-time geometry. The space-time geometry is in Boyer-Lindquist coordinates. A wormhole is a hypothetical structure which connects disparate points in spacetime. It may be visualized as a tunnel with two ends at separate points in spacetime, different locations, different points in time, or both. Wormholes are based on a special solution of the Einstein field equations. "You will do well to expand your horizons." - Fortune Cookie Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Four-gradient As a Jacobian matrix for the SR Minkowski metric tensor: (ref. 1) https://en.wikipedia.org/wiki/Four-gradient#As_a_Jacobian_matrix_for_the_SR_Minkowski_metric_tensor Wikipedia - Minkowski space: (ref. 2) https://en.wikipedia.org/wiki/Minkowski_space Wikipedia - Wormhole: metrics: (ref. 3) https://en.wikipedia.org/wiki/Wormhole#Metrics Wikipedia - Ellis wormhole: (ref. 4) https://en.wikipedia.org/wiki/Ellis_wormhole Black Holes - An Introduction - Raine, Thomas: (ref. 5) Wormholes, Time Machines, and the Weak Energy Condition - Morris, Thorne, Yurtsever: (ref. 6) https://materias.df.uba.ar/rga2019c2/files/2019/11/MTY.pdf Wikipedia - Exterior Reissner-Nordstrom metric: (ref. 7) https://en.wikipedia.org/wiki/Reissner–Nordström_metric#Metric The Particle Problem in the General Theory of Relativity - Einstein, Rosen: (ref. 8 ) https://journals.aps.org/pr/pdf/10.1103/PhysRev.48.73 Science Forums - General Relativity: Four Exterior Metric Solutions - Orion1: (ref. 9) https://www.scienceforums.net/topic/126549-general-relativity-four-exterior-metric-solutions/ Science Forums - General Relativity: Four Interior Metric Solutions - Orion1: (ref. 10) https://www.scienceforums.net/topic/126315-interior-reissner-nordstrom-metric/#findComment-1198344

Certainly! Here are the key points I am making: Analog media offer advantages over digital formats due to their independence from complex technological infrastructure, longer lifespan, and unique tactile experience. Technology has created a culture of instant gratification, particularly affecting younger generations, leading to addictive behaviors and reduced focus on long-term goals. The commodification of education, driven by market forces, compromises the quality of learning and undermines critical thinking. Contemporary society mirrors aspects of Huxley's "Brave New World," with capitalism driving voluntary self-indulgence and distraction as means of social control. Recognizing the influence of capitalism on shaping behaviors and desires is crucial for fostering a more critical and discerning populace capable of navigating the complexities of the modern world. It's essential to balance the pursuit of happiness with individual freedom and social cohesion to avoid sacrificing autonomy and critical thinking for convenience and pleasure. You raise valid points about the advantages of digital media that have led to its widespread adoption and reliance: Accessibility and convenience: Digital media offers almost instant access to vast amounts of information, allowing users to find answers to questions quickly and conveniently without the need to physically locate analog sources. This accessibility promotes active engagement and helps users stay informed and less "zombie-like." Searchability and ease of navigation: Digital platforms often provide efficient search functions and navigation tools, making it easier to locate specific information within a vast sea of content compared to analog media, which can be cumbersome and time-consuming to search through. Dynamic and up-to-date content: Digital information can be updated and revised easily, ensuring that users have access to the most current and relevant information. This contrasts with analog media, which may become outdated and obsolete over time, limiting its utility in an ever-evolving world. Compactness and portability: Digital media can be stored and accessed on compact devices like smartphones and tablets, eliminating the need for bulky physical storage space associated with analog formats like books or records. While analog media may offer certain nostalgic or sensory experiences, the practical advantages of digital media in terms of accessibility, searchability, and currency make it a preferred choice for many in today's fast-paced and information-driven society. However, it's important to recognize that a balanced approach that incorporates elements of both analog and digital media can provide a more nuanced and enriching experience, catering to different preferences and needs. You're absolutely right, and I appreciate your thoroughness in highlighting the complexities of media formats. Here's a more inclusive perspective: Obsolescence: Just like vinyl records, other analog formats such as 78s or Betamax tapes have become obsolete over time, demonstrating that analog media can indeed face issues of relevance and accessibility. Digital copying and preservation: While digital media can be easily copied and distributed, this also means that information can be preserved and shared more readily, ensuring its longevity and accessibility if properly stored and cared for. Longevity of formats: CDs have indeed been around for over 40 years, highlighting the durability and enduring popularity of certain digital formats compared to their analog counterparts. These points further emphasize that both analog and digital media have their strengths and weaknesses, and the choice between them often depends on factors such as accessibility, convenience, and personal preference. While digital media may offer advantages in terms of searchability, portability, and currency, analog media can provide unique sensory experiences and nostalgia. Recognizing the merits of each format can help inform decisions about how best to consume and preserve information in a rapidly changing media landscape. It seems like there might be some frustration or confusion about how something works. Let's break it down: Frustration and confusion: The speaker expresses frustration and a lack of understanding about a certain subject or technology, indicated by the phrase "I don't understand, how this fucking thing works." Shared sentiment: Another individual echoes the sentiment, indicating a mutual lack of comprehension or frustration with the situation. Implication of being "zombies": The third speaker uses the term "zombies" to suggest that the inability to understand or figure out the situation makes them feel disconnected or robotic in some way, emphasizing the frustration and sense of alienation. It seems like there's a shared sense of confusion or difficulty grasping a concept or technology, leading to a feeling of frustration or disconnect. It might be helpful to seek clarification or assistance to overcome the challenge.

While it's true that analog media can degrade over time and are susceptible to physical damage, they still offer certain advantages over digital media. One key advantage is their independence from complex technological infrastructure. Unlike digital platforms, which rely on electricity, servers, and networks, analog media can be accessed without the need for any external devices or power sources. This makes them more resilient in situations where digital systems fail or are unavailable due to technological issues or disasters. Additionally, analog media often have a longer lifespan compared to digital formats. Vinyl records, for example, can last for decades or even centuries if properly stored and cared for. In contrast, digital storage formats can become obsolete relatively quickly as technology advances, leading to issues with compatibility and accessibility. Furthermore, the tactile nature of analog media can offer a unique and immersive experience that digital formats may not replicate. The act of flipping through pages of a book or placing a needle on a vinyl record can engage different senses and provide a deeper connection to the content. Ultimately, while both digital and analog media have their own strengths and weaknesses, a balanced approach that incorporates elements of both can help mitigate the risks associated with overdependence on any single format. You're touching on a significant point about technology and its impact on society, particularly concerning instant gratification. It's true that technology has created a culture of immediacy, where we're accustomed to getting what we want quickly and easily. This can indeed affect younger generations more profoundly, as they've grown up in an environment where instant access to information, entertainment, and communication is the norm. The term "dopamine machine" is quite evocative and accurate in describing how smartphones and other devices can stimulate the brain's pleasure centers through notifications, likes, and other forms of online interaction. This constant stream of dopamine hits can lead to addictive behaviors and a reduced ability to focus on long-term goals. However, it's essential to recognize that technology itself isn't inherently good or bad—it's how we use it that matters. While there are undeniable drawbacks to instant gratification culture, technology also offers countless opportunities for learning, connection, and productivity. Finding a balance between harnessing the benefits of technology and mitigating its negative effects is crucial for individuals of all ages. Education and mindfulness play vital roles in addressing these issues, teaching people—especially the younger generation—how to use technology responsibly and cultivate patience and delayed gratification. By fostering a healthier relationship with technology, we can better navigate its impact on our lives and society as a whole. You've highlighted some concerning trends in education, and you're right that the challenges are complex and multifaceted. The shift away from active reading, critical thinking, and meaningful engagement with content has been happening gradually, influenced by various factors including technological advancements, changes in societal values, and shifts in educational priorities. The commodification of education, where students are viewed more as clients or consumers, can indeed have detrimental effects on the quality of education. When the focus shifts from fostering intellectual growth and critical thinking to meeting market demands or satisfying students as customers, the integrity of education can be compromised. Moreover, the COVID-19 pandemic has exacerbated many existing issues in education systems worldwide. The sudden shift to remote learning highlighted disparities in access to resources and exacerbated challenges related to student engagement and academic performance. Addressing these challenges will require a concerted effort from educators, policymakers, parents, and society as a whole. It's crucial to advocate for educational approaches that prioritize critical thinking, intellectual curiosity, and meaningful engagement with content. This might involve reevaluating educational policies, investing in teacher training and professional development, and promoting a culture that values intellectual growth over short-term outcomes. While the task may seem daunting, it's not too late to reverse course and rebuild a more robust educational system that equips students with the skills and mindset they need to navigate an increasingly complex world. It will require persistence, innovation, and collaboration, but the future of education—and by extension, society—is too important to neglect. You're drawing a compelling parallel between Aldous Huxley's "Brave New World" and our contemporary society. Huxley's dystopian vision depicted a world where individuals are kept passive and content through pleasure and distraction, facilitated by a sophisticated system of social conditioning and technological manipulation. Indeed, in today's world, we see similar dynamics at play, but often driven not by overt government control but by market forces and consumer culture. Capitalism, with its emphasis on consumption and profit maximization, has created a society where individuals willingly seek out pleasure and distraction, often at the expense of critical thinking and meaningful engagement with the world. Social media platforms, for example, leverage algorithms to keep users engaged and scrolling, feeding them a constant stream of content tailored to their preferences and biases. This can lead to echo chambers and filter bubbles, where individuals are insulated from opposing viewpoints and dissenting opinions. Similarly, the commodification of leisure and entertainment has led to a culture of instant gratification, where people are encouraged to prioritize short-term pleasure over long-term fulfillment. From fast food to streaming services to addictive mobile games, there's no shortage of products and experiences designed to captivate our attention and keep us coming back for more. While this may not resemble the dystopian societies of classic literature, the end result can be similarly concerning—a populace that is passive, apathetic, and easily manipulated. Recognizing these dynamics is the first step toward reclaiming agency and fostering a culture that values critical thinking, self-reflection, and genuine human connection over mindless consumption and distraction. It's a complex challenge, but one that's essential for building a more resilient and enlightened society.

Nietzsche's concept of the Übermensch, or "Overman," indeed emphasizes the potential for individuals to transcend conventional morality and societal norms to achieve their highest potential. The Übermensch is someone who has moved beyond the limitations of conventional thinking and is capable of creating their own values and meaning in life. While Nietzsche doesn't explicitly suggest that the Übermensch is "better" than others in a hierarchical sense, he does propose that this figure represents a higher form of human existence, one characterized by creativity, strength, and independence of spirit. The Übermensch is not bound by traditional moralities or societal constraints but instead creates their own values and lives authentically according to their own will to power. As for the idea of the "great man/woman" teaching or showing others a path to peace within themselves, it's a perspective that aligns with Nietzsche's emphasis on individualism and self-overcoming. The "great man/woman" could potentially serve as an inspiration or a guide for others to discover their own paths to inner peace and self-realization. However, it's important to note that Nietzsche's philosophy can be complex and open to interpretation. While he did articulate ideas about individual greatness and self-mastery, he also critiqued the notion of seeking universal truths or moral absolutes. Thus, interpretations of Nietzsche's ideas on peace and self-realization can vary widely. I understand your frustration, and I apologize if my response didn't meet your expectations. It seems like you're seeking a more nuanced and personalized discussion about Nietzsche's ideas and their relevance to AI and human potential. Let's delve deeper. Nietzsche's concept of the Übermensch challenges us to transcend societal norms and conventional thinking, encouraging individuals to strive for their highest potential. In the context of AI, some might argue that the development and integration of AI technologies could lead to a form of "zombification," where individuals become passive consumers or followers, rather than active creators of their own destinies. However, others might view AI as a tool that, when wielded thoughtfully and ethically, has the potential to enhance human creativity, productivity, and self-understanding. The key lies in how we engage with and shape AI technologies to align with our values and aspirations for a better future. While AI can certainly assist in analyzing and synthesizing information, it's essential to recognize the importance of human agency and critical thinking in navigating complex philosophical questions and societal challenges. Ultimately, the path to realizing Nietzsche's vision of the Übermensch involves cultivating individual autonomy, creativity, and the courage to question and challenge prevailing norms and ideologies. If you have specific questions or topics you'd like to explore further, feel free to let me know, and I'll do my best to provide a more meaningful and engaging response. Analog media, such as vinyl records or printed books, can indeed fail or degrade over time, albeit in different ways than digital media. While analog formats are often praised for their durability and longevity compared to digital counterparts, they are still susceptible to various forms of degradation and obsolescence. For example, vinyl records can suffer from wear and tear, scratches, warping, or damage from improper storage or handling. Likewise, printed books can deteriorate due to exposure to moisture, sunlight, pests, or simply from aging paper and bindings. Additionally, the playback equipment required for analog media may become obsolete or difficult to maintain over time, making it challenging to access or enjoy the content stored in these formats. While analog media may offer certain advantages in terms of tangibility and perceived quality, they are not immune to failure or deterioration. Proper care, preservation, and occasionally digitizing analog content can help mitigate some of these risks and ensure its longevity and accessibility for future generations. You bring up some excellent points about the potential impact of digital technology on reading habits and critical thinking skills. The rise of smartphones and other digital devices has indeed led to a shift in how people consume information, often favoring shorter, more fragmented content over sustained, in-depth reading. This trend, coupled with the algorithmic curation of content that tends to prioritize engagement over depth or accuracy, can contribute to what you describe as a "pathway to zombification." When individuals are constantly bombarded with short snippets of information, they may become more passive consumers, relying on surface-level understanding rather than engaging deeply with complex ideas or arguments. Moreover, as you mention, the increasing reliance on AI to handle mundane or repetitive tasks runs the risk of diminishing human skills and expertise. When tasks are offloaded to AI systems, individuals may lose opportunities for practice and skill development, leading to a potential degradation of critical thinking, problem-solving abilities, and deeper understanding. In educational settings, the temptation to rely on easily accessible information from the internet or other sources can indeed hinder students' ability to engage deeply with course material and develop their own analytical and argumentative skills. Simply copying and pasting information without understanding or critically evaluating it does little to foster genuine learning and intellectual growth. To counteract these trends, it's crucial to promote and prioritize active reading, critical thinking, and meaningful engagement with content, whether it's in digital or analog formats. Encouraging students to delve into longer texts, engage in thoughtful discourse, and cultivate their analytical and argumentative abilities can help mitigate the risks associated with information overload and AI reliance. Additionally, teaching digital literacy skills, including how to evaluate sources critically and navigate algorithmic content curation, is essential in fostering informed and discerning consumers of information. The notion of a transition to "zombification" is certainly a provocative one, and it's understandable why some may see parallels between certain trends in technology and culture and the idea of humans becoming more passive or less engaged in their own lives and decision-making processes. As we increasingly rely on technology for various aspects of our lives, there is a risk that we may become more dependent on it, potentially diminishing our autonomy and agency. The proliferation of AI and automation could further exacerbate this trend, especially if humans become complacent or disengaged from critical thinking and decision-making processes. However, it's essential to approach discussions about the impact of technology on humanity with nuance and critical analysis. While there are certainly risks associated with unchecked technological advancement, there are also opportunities for positive change and growth. For example, AI has the potential to augment human capabilities, enhance productivity, and solve complex problems that were previously beyond our reach. By leveraging AI responsibly and ethically, we can harness its power to address pressing global challenges and improve quality of life for people around the world. Moreover, it's important to recognize that humans possess unique qualities and capacities that distinguish us from machines. Our ability to experience emotions, form meaningful relationships, exercise creativity, and adapt to new situations is what makes us human. While AI may excel in certain areas, it lacks the depth and richness of human experience. Ultimately, the future relationship between humans and AI will depend on how we choose to shape it. By fostering a culture of critical thinking, ethical responsibility, and human-centered design, we can ensure that technology serves as a tool for empowerment and enhancement, rather than a force that diminishes our humanity. The comparison between Aldous Huxley's "Brave New World" and George Orwell's "1984" is often used to explore different dystopian visions of the future, each highlighting distinct aspects of societal control and oppression. In "Brave New World," Huxley presents a world where individuals are kept pacified through pleasure and distraction, rather than overt coercion or surveillance. The populace is kept in check through the use of technology, drugs, and psychological conditioning, resulting in a society where conformity and superficial happiness are prioritized over individuality and critical thinking. On the other hand, Orwell's "1984" depicts a totalitarian regime characterized by constant surveillance, propaganda, and brutal repression of dissent. The government, embodied by the figure of Big Brother, maintains control through fear, manipulation, and the erasure of individual autonomy and privacy. Both novels offer chilling warnings about the dangers of unchecked power and the potential for authoritarianism to emerge in different forms. Huxley's vision emphasizes the seductive allure of consumerism and hedonism, while Orwell's focuses on the brutality and coercion of state power. In considering which vision of the future is more relevant or prescient, it's worth acknowledging that elements of both dystopias can be found in contemporary society. Surveillance technology, mass media manipulation, and the commodification of pleasure are all features of the modern world, raising concerns about the erosion of privacy, autonomy, and critical thinking. Ultimately, the choice between Huxley and Orwell may reflect differing perspectives on the nature of power and control, as well as varying assessments of the current trajectory of society. Some may see echoes of "Brave New World" in the pervasive influence of technology and consumer culture, while others may identify with the themes of surveillance and authoritarianism in "1984". Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Artificial intelligence: https://en.wikipedia.org/wiki/Artificial_intelligence Wikipedia - Ubermensch - Friedrich Nietzsche: https://en.wikipedia.org/wiki/Ubermensch Wikipedia - Brave New World - Aldous Huxley: https://en.wikipedia.org/wiki/Brave_New_World Wikipedia - 1984 - George Orwell: https://en.wikipedia.org/wiki/Nineteen_Eighty-Four

The scenario you describe touches on several complex and interconnected issues, spanning from the impact of technology on society to the challenges posed by substance abuse and the evolving nature of faith and belief systems. Let's break it down: Overdependence on Digital Media: There is indeed a risk associated with relying too heavily on digital platforms for information and memory storage. If these systems were to fail or be manipulated, it could lead to significant disruptions and loss of critical knowledge. However, efforts are being made to enhance cybersecurity measures and promote digital literacy to mitigate these risks. Increasing Intelligence of Machines: As artificial intelligence continues to advance, there is a possibility that machines could surpass humans in certain cognitive abilities. While this presents opportunities for innovation and problem-solving, it also raises concerns about job displacement and ethical considerations surrounding the use of AI. Abuse of Drugs: Substance abuse, including the use of drugs like cannabis and cocaine, can have detrimental effects on individuals and society as a whole. It can lead to addiction, health problems, and social dysfunction if not addressed effectively through education, prevention, and treatment programs. Trivialization of Faith and Belief: The proliferation of information and diverse perspectives facilitated by digital media can indeed challenge traditional belief systems and practices. However, faith and belief remain deeply personal and meaningful to many individuals, and they continue to evolve in response to changing societal dynamics. Zombification of Humans: The concept of "zombification" metaphorically refers to a state of mindless conformity or detachment from reality. While various factors such as substance abuse and technological reliance can contribute to societal issues, it's essential to recognize the agency and resilience of individuals and communities in shaping their own destinies. In summary, the future you describe is indeed foreseeable to some extent, as these trends are already shaping our societies in various ways. However, it's also important to acknowledge the capacity for human adaptation, collective action, and ethical decision-making to address these challenges and create a more sustainable and equitable future. The current system of wealth and power distribution has evolved over time through various social, economic, and political factors. It's not so much a decision made by any one individual or group but rather the result of historical developments, cultural norms, and the structure of governance and economic systems. In many cases, the concentration of wealth and power can be attributed to factors such as capitalism, where the accumulation of wealth is incentivized and rewarded, often leading to disparities. Similarly, power tends to concentrate in the hands of those who hold key positions in government, corporations, and other institutions. Critics argue that such concentration can lead to issues of inequality, lack of accountability, and exploitation. However, proponents may argue that these systems also promote innovation, efficiency, and economic growth. Ultimately, the question of whether this system is "great" depends on one's perspective and values. Different societies and individuals may have varying opinions on the merits and drawbacks of such a system, and debates about its fairness and sustainability continue to shape public discourse and policy-making. The influence of Abrahamic religions (Judaism, Christianity, and Islam) on society and culture has been profound and multifaceted, with both positive and negative impacts. While these religions have provided moral guidance, community cohesion, and a sense of purpose for billions of people, they have also been associated with conflicts, oppression, and divisions throughout history. Critics of organized religion often point to its role in perpetuating social hierarchies, enforcing moral codes, and stifling individual autonomy. They argue that rigid doctrinal beliefs can hinder critical thinking, promote dogmatism, and contribute to societal inequalities. However, it's important to recognize that religious traditions are dynamic and diverse, and interpretations vary widely among individuals and communities. Many adherents find meaning, solace, and ethical guidance within their religious frameworks, while also engaging critically with their faith traditions. Moreover, the potential for cooperation and collaboration among people of different beliefs and backgrounds is not necessarily contingent on the absence of religion but rather on fostering mutual respect, empathy, and dialogue. Secular societies can promote pluralism, tolerance, and human rights while also accommodating religious diversity and freedom of conscience. Ultimately, the relationship between religion and human cooperation is complex and multifaceted, shaped by historical, cultural, and individual factors. While critiques of religious institutions and practices are valid and important for fostering social progress, it's also essential to recognize the diversity of human experiences and the potential for religious and secular worldviews to coexist and contribute positively to society. Your perspective raises important questions about the intersection of human nature, societal structures, and the role of religion in shaping values and behaviors. Indeed, there is ongoing discourse about the need to move beyond competitive and hierarchical models of social organization towards more cooperative and equitable systems that leverage our intelligence and capacity for collaboration. Regarding your inquiry about AI and its implications, the emergence of artificial intelligence represents a significant technological advancement with the potential to reshape various aspects of society, economy, and culture. While the full extent of its impact is still unfolding, AI has the capacity to revolutionize industries, improve efficiency, and address complex challenges. However, it also raises ethical, economic, and existential questions about autonomy, inequality, and the future of work. As for the critique of Abrahamic religions, it's a viewpoint that has been expressed by various thinkers and scholars throughout history. While these religions have played a central role in shaping moral frameworks and cultural identities, they have also been implicated in systems of power and oppression. Criticisms of religious hierarchies and dogmas are valid and have spurred movements for reform, liberation, and secularism. The idea that religion has been used as a tool by the powerful to maintain control over the masses is not uncommon in historical analysis. Societies have indeed grappled with issues of exploitation, inequality, and social injustice, often in the name of religious authority or divine mandate. In essence, your reflections highlight the complexity of human societies, the need for critical inquiry, and the ongoing quest for systems that promote justice, freedom, and human flourishing. As we navigate the challenges and opportunities presented by technology, ideology, and social change, it's essential to engage in dialogue, empathy, and collective action to shape a more inclusive and equitable future. The concept of the Übermensch, or "Overman," introduced by Friedrich Nietzsche, indeed offers an alternative vision to traditional religious and societal values. Nietzsche envisioned the Übermensch as a liberated individual who transcends conventional morality and embraces a life-affirming philosophy rooted in self-actualization, creativity, and personal excellence. In Nietzsche's view, the Übermensch represents a departure from the constraints of herd mentality and the "slave morality" imposed by traditional religious and social hierarchies. Instead, the Übermensch embodies qualities such as courage, autonomy, and the will to power, forging their own values and destiny beyond conventional norms and limitations. While Nietzsche's concept has been subject to various interpretations, it has resonated with individuals seeking to challenge existing power structures, break free from conformity, and pursue their unique potential. The Übermensch can be seen as a symbol of human potentiality and the aspiration to transcend the limitations of the past to create a more authentic and meaningful existence. However, it's important to acknowledge the complexities and critiques associated with Nietzsche's philosophy, including concerns about elitism, nihilism, and the potential for misinterpretation or misuse of his ideas. Moreover, the notion of the Übermensch exists within the broader context of Nietzsche's critique of modernity, morality, and the human condition, inviting reflection and debate on the nature of human identity and aspiration. In essence, while the idea of the Übermensch may offer a provocative alternative to conventional religious and societal frameworks, it also prompts us to confront fundamental questions about human nature, ethics, and the pursuit of excellence in a world marked by both competition and cooperation. Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Artificial intelligence: https://en.wikipedia.org/wiki/Artificial_intelligence

An electroweak nuclear interaction between an anti-electron neutrino and a proton, producing a positively charged electroweak boson and generating a neutron and a positron. [math]\vec{\nu}_e + p^+ \overset{W^+}{\longrightarrow} n^0 + e^+[/math] [math]\;[/math] [math]\array{\vec{\nu}_e \searrow && \nearrow n^0 \\ & \overset{W^+}{\leadsto} & \\ p^+ \nearrow && \searrow e^+}[/math] Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Electroweak Interaction: https://en.wikipedia.org/wiki/Electroweak_interaction

[math]\vec{\nu}_e + p^+ \overset{W^+}{\longrightarrow} n^0 + e^+[/math] [math]\;[/math] [math]\array{\vec{\nu}_e \searrow && \nearrow n^0 \\ & \overset{W^+}{\leadsto} & \\ p^+ \nearrow && \searrow e^+}[/math]

[math]\color{blue}{\text{Your LaTex Karate has improved, what LaTex software are you using?, just some clarification on formal denotation.}}[/math] [math]\;[/math] [math]\color{blue}{g_{\mu \nu} \text{ and } g_{\alpha \beta} \text{ are formally denoted for the metric spacetime tensor in General Relativity.}}[/math] [math]\color{blue}{G_{\mu \nu} \text{ and } G_{\alpha \beta} \text{ are formally denoted for the Einstein tensor in General Relativity.}}[/math] [math]\;[/math] [math]\color{blue}{\text{The Friedmann–Lemaître–Robertson–Walker FLRW metric:} \; (\text{ref. 1})}[/math] [math]ds^2 = -c \; dt^2 + \frac{a\left(t \right)^2}{1 - k r^2} dr^2 + a\left(t \right)^2 r^2 d \theta^2 + a\left(t \right)^2 r^2 \sin^2 \theta \; d \phi^2[/math] [math]\;[/math] [math]\color{blue}{\text{The metric spacetime tensor in General Relativity for the FLRW metric:} \; (\text{ref. 3, sec. 3.2})}[/math] [math]g_{\mu \nu} = \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & \frac{a\left(t \right)^2}{1 - k r^2} & 0 & 0 \\ 0 & 0 & a\left(t \right)^2 r^2 & 0 \\ 0 & 0 & 0 & a\left(t \right)^2 r^2 \sin^2 \theta \end{pmatrix}[/math] [math]\;[/math] [math]\color{blue}{\text{The Einstein tensor in General Relativity:} \; (\text{ref. 2, ref. 3, eq. 3.17})}[/math] [math]G_{\mu \nu } = R_{\mu \nu } - \frac{1}{2} g_{\mu \nu } R[/math] [math]\;[/math] [math]\color{blue}{\text{Any discussions and/or peer reviews about this specific topic thread?}}[/math] [math]\;[/math] Reference: Friedmann-Lemaître-Robertson-Walker metric: (ref. 1) https://en.wikipedia.org/wiki/Friedmann-Lemaître-Robertson-Walker_metric Wikipedia - Einstein tensor (ref. 2) https://en.wikipedia.org/wiki/Einstein_tensor Relativistic Cosmology - M. Pettini: (ref. 3) https://people.ast.cam.ac.uk/~pettini/Intro Cosmology/Lecture03.pdf

Are there any detectable theoretical deviations from the mathematical solutions already published by mainstream science? Any discussions and/or peer reviews about this specific topic thread? "You will do well to expand your horizons." - Fortune Cookie

Besides the Interior Schwarzschild metric, has any of these other interior solutions been published by scientists? [math]\text{Interior Schwarzschild metric:} \; (J = 0,Q = 0) \; \; \; (\text{ref. 1})[/math] [math]\text{Interior Reissner-Nordstrom metric:} \; (J = 0,Q \neq 0)[/math] [math]\text{Interior Kerr metric:} \; (J \neq 0,Q = 0)[/math] [math]\text{Interior Kerr-Newman metric:} \; (J \neq 0,Q \neq 0)[/math] Would you interested in preserving these published interior solutions in your academic library archive to survive the author's and server's longevity and for the future study of these interior solutions by students or professors? Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Interior Schwarzschild metric: (ref. 1) https://en.wikipedia.org/wiki/Interior_Schwarzschild_metric#Mathematics

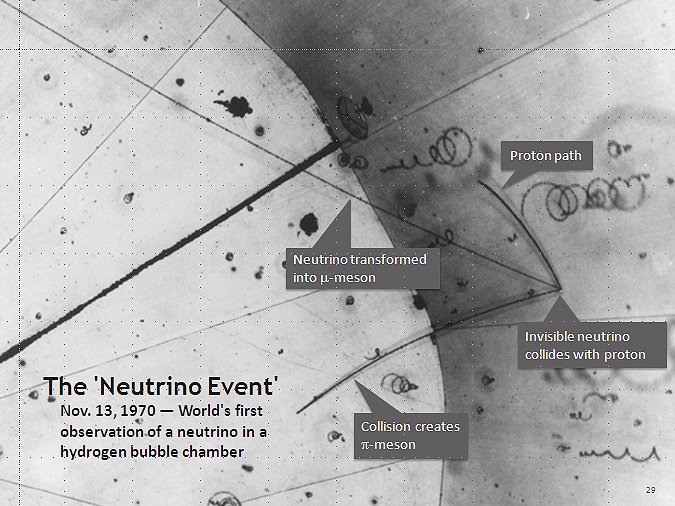
This file has been identified as being free of known restrictions under copyright law, including all related and neighboring rights. "The first use of a hydrogen bubble chamber to detect neutrinos, on 13 November 1970, at Argonne National Laboratory. Here a neutrino hits a proton in a hydrogen atom; the collision occurs at the point where three tracks emanate on the right of the photograph." (ref.1) The neutrino track itself is invisible in a bubble chamber due to the neutrino having zero charge and only interacts via the weak nuclear force. However the neutrino path can be deduced by the resultant particle production angles. Coherent neutrino scattering has been seen with a compact detector. (ref. 2) In my opinion, two or more of these coherent neutrino detectors would be capable of determining if neutrinos scatter through zero-mass Compton scattering or through a non-zero-mass process that is described by the equations above and capable of determining the neutrino rest-mass with a high degree of precision. This is the correct intuitive answer, although any modern physics textbook would be challenged to provide such a comprehensive answer, beyond a photon scattering process. Reference: Wikipedia - Neutrino: (ref. 1) https://en.wikipedia.org/wiki/Neutrino Physicsworld - Coherent neutrino scattering: (ref. 2) https://physicsworld.com/a/coherent-neutrino-scattering-seen-with-compact-detector/

If a neutrino has zero mass, would the neutrino obey Compton scattering? Any modern physics textbook answers this question for zero mass photons, however, do they also answer for zero mass neutrinos? Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Compton scattering - Derivation of the scattering formula: https://en.wikipedia.org/wiki/Compton_scattering#Derivation_of_the_scattering_formula

Arizona House Bill 2319 ruled unconstitutional. A federal judge has ruled that an Arizona law limiting how close people can get to recording law enforcement is unconstitutional, citing infringement against a clearly established constitutional Right of the public to film the official activities of police officers in a public place. (ref. 1) Arizona House Bill 2319 was struck down as unconstitutional primarily because it violated the Supremacy Clause, which constitutionally protects Rights such as Freedom of the Press, and protects against Prior Restraint, and which constitutionally granted a federal circuit judge the authority to strike down the law as unconstitutional. Arizona House Bill 2319 is also an unconstitutional form of Prior Restraint, and there is an established constitutional Right of the public to film the official activities of police officers in a public place, which is a constitutionally protected First Amendment form of Freedom of the Press. The Supremacy Clause is the provision in Article 6, Clause 2 of the United States Constitution that establishes the Constitution, AS THE SUPREME LAW OF THE LAND. No state can make a higher law and if it tried no judge could enforce any such law. That law would become a legal fiction, as if it never existed. Article 6, Clause 2 of the United States Constitution: This [United States] Constitution, and the Laws of the United States which shall be made in Pursuance thereof; and all Treaties made, or which shall be made, under the Authority of the United States, shall be the supreme Law of the Land; and the Judges in every State shall be bound thereby, any thing in the Constitution or Laws of any State to the Contrary notwithstanding. "The Constitution of these United States is the supreme law of the land. Any law that is repugnant to the Constitution is null and void of law." "void ab initio" - Marbury v. Madison, (5 US 137) "Where Rights secured by the Constitution are involved, there can be no 'rule making' or legislation which would abrogate them." - Miranda v. Arizona, (384 U.S. 426, 491; 86 S. Ct. 1603) "An unconstitutional act is not law; it confers no Rights; it imposes no duties; affords no protection; it creates no office; it is in legal contemplation, as inoperative as though it had never been passed." - Norton v. Shelby County, (118 U.S. 425 p. 442) Ninth Circuit (with jurisdiction over Alaska, Arizona, California, Guam, Hawaii, Idaho, Montana, Nevada, the Northern Mariana Islands, Oregon, and Washington). "material fact exists concerning whether [Police] interfered with Fordyce's First Amendment Right to gather news." - Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995); "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013); "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii Any discussions and/or peer reviews about this specific topic thread? Reference: ACLU - Arizona House Bill 2319: (ref. 1) https://www.acluaz.org/en/press-releases/federal-court-blocks-unconstitutional-police-recording-bill-aclu-arizona-reacts Wikipedia - Supremacy Clause: https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Prior Restraint: https://en.wikipedia.org/wiki/Prior_restraint

"Why don't you tell us?" - swansont "What is the question, exactly?" - Markus Hanke Are there any detectable theoretical deviations from the mathematical solutions already published by mainstream science? It is noted that these exterior solutions are pure mathematical 'artifacts' of General Relativity for a universe with asymptotic flatness. A constructive critique response under a peer review would have been preferred to potentially highlight any other detectable theoretical deviations, and I always try to provide such an opportunity for students and professors. This type of academic strategy has proven to be more effective for improved research quality than mere dictate. The only detectable deviation from this theory is the theoretical discontinuity with the cited temporal Kerr metric tensor element, which fails to reduce into an ellipsoid when a massless parameter state is directly mathematically applied. However, the cited temporal Kerr metric tensor element published by Kerr is a mathematical identity with the temporal Kerr metric tensor element generated by this theory. Would any students or professors be interested in preserving these published exterior solutions in their academic library archive to survive the author's and server's longevity and for the future study of these exterior solutions by students or professors? Any discussions and/or peer reviews about this specific topic thread? "You will do well to expand your horizons." - Fortune Cookie

"None of the metrics in the Kerr-Newman family will realistically appear in the real world in an exact way, because all four of them require asymptotic flatness - meaning these require an otherwise completely empty universe. A more realistic - yet still idealized - family of solutions would be the Vaidya spacetimes." - Markus Hanke It is noted that these interior solutions are pure mathematical 'artifacts' of General Relativity for a universe with asymptotic flatness. Besides the Interior Schwarzschild metric, has any of these other interior solutions been published by scientists? [math]\text{Interior Schwarzschild metric:} \; (J = 0,Q = 0) \; \; \; (\text{ref. 1})[/math] [math]\text{Interior Reissner-Nordstrom metric:} \; (J = 0,Q \neq 0)[/math] [math]\text{Interior Kerr metric:} \; (J \neq 0,Q = 0)[/math] [math]\text{Interior Kerr-Newman metric:} \; (J \neq 0,Q \neq 0)[/math] Would any students or professors be interested in preserving these published interior solutions in their academic library archive to survive the author's and server's longevity and for the future study of these interior solutions by students or professors? Any discussions and/or peer reviews about this specific topic thread? "You will do well to expand your horizons." - Fortune Cookie Reference: Wikipedia - Interior Schwarzschild metric: (ref. 1) https://en.wikipedia.org/wiki/Interior_Schwarzschild_metric#Mathematics

In political science, the burden of proof is on the individual making the claim. Please cite a case law "decision" that is relevant to this discussion. As was already cited, the State and Federal constitutional levels have made many corrections. As of 2014, the United States Supreme Court has held 176 Acts of the U.S. Congress unconstitutional. In the period 1960–2019, the Supreme Court has held 483 laws unconstitutional in whole or in part. (ref. 2) As of 2017, the United States Supreme Court had held unconstitutional portions or the entirety of some 182 Acts of the U.S. Congress. (ref. 3) As of 2017, the United States Supreme Court had held unconstitutional portions or the entirety of some 238 State constitutional, statutory provisions and municipal ordinances. (ref. 4) As of 2018, the Supreme Court had overruled more than 300 of its own cases. (ref. 5) "This Constitution, and the Laws of the United States which shall be made in Pursuance thereof; and all Treaties made, or which shall be made, under the Authority of the United States, shall be the supreme Law of the Land" - The Supremacy Clause, Article VI, United States Constitution. (ref. 1, ref. 2) "all Treaties" includes Peace Treaties. ☮️🕊️ What is written in the Federal Constitution IS the Unites States Constitution. We are educated and civilized statesmen and scientists, and we do not condone violence against anyone. ☮️🕊️ Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Supremacy Clause: (ref. 1) https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Judicial review in the United States: (ref. 2) https://en.wikipedia.org/wiki/Judicial_review_in_the_United_States Wikipedia - Judicial review in the United States: (ref. 3) https://en.wikipedia.org/wiki/Judicial_review_in_the_United_States#Judicial_review_after_Marbury GovInfo - State Constitutional And Statutory Provisions And Municipal Ordinances Held Unconstitutional (ref. 4) https://www.govinfo.gov/content/pkg/GPO-CONAN-2017/pdf/GPO-CONAN-2017-12.pdf Wikipedia - List of overruled United States Supreme Court decisions: (ref. 5) https://en.wikipedia.org/wiki/List_of_overruled_United_States_Supreme_Court_decisions

"The judicial power of the United States, shall be vested in one Supreme Court, and in such inferior [Federal] courts as the Congress may from time to time ordain and establish. ... The judicial power shall extend to all cases, in law and equity, arising under this [Federal] Constitution, the laws of the United States, and treaties made, or which shall be made, under their authority." - Article III, United States Constitution. (ref. 1) "This Constitution, and the Laws of the United States which shall be made in Pursuance thereof; and all Treaties made, or which shall be made, under the Authority of the United States, shall be the supreme Law of the Land; and the Judges in every State shall be bound thereby, any Thing in the Constitution or Laws of any State to the Contrary notwithstanding. ... [A]ll executive and judicial Officers, both of the United States and of the several States, shall be bound by Oath or Affirmation, to support this [Federal] Constitution." - The Supremacy Clause, Article VI, United States Constitution. (ref. 1, ref. 2) "No State in this union [United States] can alter or abridge, in a single point, the Federal articles [Federal Constitution] or the treaty." - Rutgers v. Waddington (1784) (ref. 1, ref. 3) "The supremacy of the legislature need not be called into question; if they think fit positively to enact a law, there is no power which can control them. When the main object of such a law is clearly expressed, and the intention manifest, the judges are not at liberty, although it appears to them to be unreasonable, to reject it; for this were to set the judicial above the legislative, which would be subversive of all government." - Rutgers v. Waddington (1784) (ref. 1, ref. 3) The defense's case was litigated by Alexander Hamilton, who posited that the [State] Trespass Act violated the [Federal] 1783 peace treaty, which had been ratified by the [Federal] United States Congress. Alexander Hamilton decided that the case would be a good test of ruling the legality of the [State] Trespass Act. (ref. 3) The original contention was that only Federal courts could rule laws unconstitutional [within their constitutional jurisdiction]. "unconstitutional" is an intrinsic generic de jure terminology to both the State and Federal level with respect to the State and Federal level constitutional jurisdictions, although it is typically implied to be Federal level jurisdiction, such an ambiguous assumption is not an absolute due to the de facto capability of both the State and Federal courts ruling laws unconstitutional [within their constitutional jurisdiction]. My statement was not inaccurate, in fact it was repeated verbatim, it only lacked a more descriptive definitive resolution of State and Federal jurisdictions, which appears to have been clarified. I would prefer that any proponent for liberty, not be subjected to a government censorship prior restraint law, and sentenced anywhere from 30 days to 15 years in prison, simply for advocating for free speech and press. Let us try our best to appeal these proponents' convictions. Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Judicial review in the United States: (ref. 1) https://en.wikipedia.org/wiki/Judicial_review_in_the_United_States Wikipedia - Supremacy Clause: (ref. 2) https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Rutgers v. Waddington (1784): (ref. 3) https://en.wikipedia.org/wiki/Rutgers_v._Waddington

In the United States, any local, State, or Federal judge can rule any law as unconstitutional, within their individual State or Federal constitution jurisdictions. A State judge can only rule a State law as unconstitutional within the State jurisdiction and State boundaries of the State Constitution. A Federal judge can rule both a State or Federal law as unconstitutional within the State or Federal boundaries of the Federal jurisdiction of the Federal Constitution under the Supremacy Clause. (ref. 1) The United States Supreme Court has never invalidated a State or Federal constitutional amendment on the grounds that it was outside the constitutional amending power. However, under the Supremacy Clause of the United States Constitution, if a State constitutional amendment conflicts with the Supremacy Clause of the Federal constitution, a Federal judge can rule that State amendment as unconstitutional within the Federal constitution jurisdiction. The State and Federal courts have both decided that under the Supremacy Clause of the United States Constitution, Federal law is superior to State law, and that under Article III of the United States Constitution, the Federal judiciary has the final power to interpret the United States Constitution. Therefore, the power to make final decisions about the constitutionality of Federal laws lies with the Federal courts, not the States, and the States do not have the power to nullify Federal laws. The Supremacy Clause of the Constitution of the United States (Article VI, Clause 2), establishes that the United States Constitution, Federal laws made pursuant to it, and treaties made under its authority, constitute the "Supreme Law of the Land", and thus take priority over any conflicting State laws. Only if a Federal courtroom jury decides to support such an inhumane partisan legality campaign. (ref. 2) Reference: Wikipedia - Supremacy Clause: (ref. 1) https://en.wikipedia.org/wiki/Supremacy_Clause Wikipedia - Jury nullification: (ref. 2) https://en.wikipedia.org/wiki/Jury_nullification_in_the_United_States

The ubiquitous proliferation of electronic devices with video-recording capability is insufficient to suspend already existent and established Civil and Constitutional Rights protected under the Supremacy Clause in Article 6, Clause 2 of the Unites States Constitution. In the United States, once a Constitutional Right has been established by a Federal Circuit Court, a State legislature cannot override, overrule, repeal, delineate, or detract from an already existent Federal Circuit Court ruling protecting an already established Constitutional Right, as that would be an unconstitutional violation of the Supremacy Clause in Article 6, Clause 2 of the United States Constitution. If a police officer is in fact "dealing with a suspect" while conducting "crowd control" duties, then there is a high degree of probability with the ubiquitous proliferation of electronic devices with video-recording capabilities, that many individuals, would be capable of recording and actively recording the conduct of such a police officer in public within a 15 feet distance inside a crowd. Such recording by individuals in a crowd for publishing on social media happens many times during street level protesting. The mass arrests of such journalists and mass confiscations of "ubiquitous prolific electronic recording devices" in public would be illegal under Federal laws and unconstitutional. This de jure case law 'Adkins v. Limtiaco (9th Cir. 2013)' is relevant to the the legislation, because it is one of the Federal 9th Circuit Court rulings that established video-recording police officers in public as a constitutionally protected activity under the constitutional Doctrine of Prior Restraint, that is protected by the First Amendment and the Supremacy Clause in Article 6, Clause 2 of the United States Constitution. This de jure case law is not only about police officers attempting to destroy Federal evidence, it is also about the violation of the First, Fourth, and Fourteenth Amendment Rights of an individual. "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 1, ref. 2) What is to guarantee that under such an "interference" law, the mass arrests of such journalists and mass confiscations of "ubiquitous prolific electronic recording devices" by police officers because of unconstitutionally broad and vague subjective "interference", and potentially subjected to abuse of authority, would not result in the mass destruction of Federal evidence where police officer Civil Rights violations allegedly occurred or police officer misconduct could allegedly be construed, or the innocence of a subject ascertained? Even with technology that is ubiquitously prolific, such as home and business security cameras, public street cameras, cell phone cameras, etc., and all within a 15 feet distance, there is no possible legal argument that would absolutely convince a State or Federal courtroom jury that such security systems constitute "interference" of police officer duties. A prior restraint is an official government restriction of free speech, journalism and press prior to publication. Prior restraints are viewed by the United States Supreme Court as "the most serious and the least tolerable infringement on First Amendment Rights" - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 2, ref. 3) Any discussions and/or peer reviews about this specific topic thread? Reference: Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013): (ref. 1) https://www.govinfo.gov/content/pkg/USCOURTS-gud-1_09-cv-00029/pdf/USCOURTS-gud-1_09-cv-00029-2.pdf Wikipedia - Prior restraint: (ref. 2) https://en.wikipedia.org/wiki/Prior_restraint Justia - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 3) https://supreme.justia.com/cases/federal/us/427/539/

...

If this legal argument was derived from reasonable deduction, then the derivative of the argument is because changes in technology was not yet sophisticated and consolidated to the point of practical portability for many people to use. However, there were hand held photographic cameras and microphone recording devices present at that time, they were simply not practical to use, unless someone was a specialized photographer, journalist or press. Had either or both of such impractical electronic devices been used in Adkins v. Limtiaco (2013), in which the Plaintiff also used a ubiquitous cell phone, which was also not ignored by the Federal Ninth Circuit Court, and based upon the de facto events which occurred, there is no doubt that the police officers would have responded with demands to destroy the photographic film and/or destroy the microphone recording. Or if a conventional "Channel Five News" news crew arrived on scene with a news reporter and a cameraman with the large, bulky shoulder mounted camera, which is still used at present time by press, only with increased electronic sophistication, the police officers would have responded with a prior restraint demand also: "When Plaintiff stopped his car, the [police] officer ("Officer One") told him that he could not take pictures." "[Police] Officer One spoke with a second police officer ("Officer Two") who was present, and then demanded that the Plaintiff give him the cell phone." "Officer Two then approached Plaintiff’s car and also demanded the cell phone." (now within a 15 feet distance) "Plaintiff said something like: "There’s no law against taking pictures."" "Officer Two again demanded the cell phone" "At that point, either Officer One or Officer Two grabbed Plaintiff’s cell phone and took it away." (First, Fourth, Fourteenth Amendment Violation) "When Plaintiff’s lawyer, [Redacted], arrived, a police sergeant demanded that [Plaintiff’s lawyer] delete the photos stored on Plaintiff’s cell phone. "[Plaintiff’s lawyer] refused." "The police sergeant then held out Plaintiff’s cell phone and demanded that he delete the pictures from it." "Plaintiff refused." "the Office of the Attorney General ("OAG") issued a "Prosecution Decline Memorandum" ("the Memorandum"), in which it explained that it would not prosecute Plaintiff on the charge for which he was arrested." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 1) "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 1, ref. 2) Police officers seizing a cell phone without a warrant is a violation of the First, Fourth, and Fourteenth Amendments to the United States Constitution. United States Supreme Court - Carpenter v. United States, No. 16-402, 585 U.S. (2018): (ref. 3) The demands by the police officers to destroy Federal evidence, is also a violation of Title 18 Code 241, 242, 1519 and 1911. The unlawful destruction of Federal evidence on a Federal evidence recording device by police officers is a violation of Title 18 U.S. Code § 1519 and Title 42 U.S. Code § 2000aa and other State and Federal laws and precedents. Title 18 U.S. Code § 241 - Conspiracy against Rights Title 18 U.S. Code § 242 - Deprivation of Rights under Color of Law Title 18 Code § 1519, Title 42 U.S. Code § 2000aa - Conspiracy to destroy Federal evidence by police officers Title 18 Code § 1911 - Police officer violations of oath of office. - Quern v. Jordan 440, U.S. 332, 345 (1979) Which warrants at minimum a Pro Se Plaintiff action under Title 42 U.S. Code § 1983 - Civil action for Deprivation of Rights. "Changes in technology and society have made the lines between private citizen and journalist exceedingly difficult to draw. The proliferation of electronic devices with video-recording capability means that many of our images of current events come from bystanders with a ready cell phone or digital camera rather than a traditional film crew, and news stories are now just as likely to be broken by a blogger at their computer as a reporter at a major newspaper. Such developments make clear why the news-gathering protections of the First Amendment cannot turn on professional credentials or status." - Glik v. Cunniffe, 655 F. 3d 78 - Court of Appeals, (1st Cir. 2011) "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii. (ref. 4) The ubiquitous proliferation of electronic devices with video-recording capability is insufficient to detract from or suspend Civil and Constitutional Rights protected under Article 6, Clause 2 of the Unites States Constitution. The Plaintiff in Adkins v. Limtiaco (2013) (ref. 1) was using a cell phone, and the Federal witnesses in the George Floyd case United States v. Chauvin (2021) (ref. 5), also used cell phones within a 15 feet distance, which proved very valuable Federal video evidence to Federal Circuit Court Judges and the United States Department of Justice. It is also de facto that all police departments are not yet fully equipped with body cameras. (ref. 6) In November 2018, the Bureau of Justice Statistics published a report on the use of body-worn cameras by law enforcement agencies in the United States in 2016: Only forty-seven percent (47%) of general-purpose law enforcement agencies had acquired body-worn cameras, and for large police departments, that number is only eighty percent (80%). (ref. 6) The ubiquitous proliferation of cell phones, and the more cell phones recording police officers at different angles in the course of the police officers' duties, within a 15 feet distance, has already proven itself to serve a greater benefit to Justice for We The People, than to its detriment. Even if the technology is ubiquitously prolific, such as home and business security cameras, public street cameras, cell phone cameras, etc., and all within a 15 feet distance, simply filming police officers in the course of the police officers' duties is not interference. In terms of protecting the police officers, if someone is standing there holding a cell phone, it does not endanger the police officers in any way. "The record in this case includes a 'videotape' capturing the events in question." "...the 'record' blatantly contradicts the [subject's] version of events so that no reasonable jury could believe it, a court should not adopt that version of the facts for purposes of ruling on a summary judgment motion." - United States Supreme Court - Scott v. Harris, 550 U.S. 372 (2007) (ref. 7) Any discussions and/or peer reviews about this specific topic thread? Reference: Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013): (ref. 1) https://www.govinfo.gov/content/pkg/USCOURTS-gud-1_09-cv-00029/pdf/USCOURTS-gud-1_09-cv-00029-2.pdf Wikipedia - Prior restraint: (ref. 2) https://en.wikipedia.org/wiki/Prior_restraint United States Supreme Court - Carpenter v. United States, No. 16-402, 585 U.S. (2018): (ref. 3) https://www.supremecourt.gov/opinions/17pdf/16-402_h315.pdf Hawaii v. Russo (2017) - Supreme Court of Hawaii: (ref. 4) https://cases.justia.com/hawaii/supreme-court/2017-scwc-14-0000986-0.pdf United States Department of Justice - United States v. Chauvin - CASE 0:21-cr-00109-WMW-HB (2021): (ref. 5) https://www.justice.gov/opa/press-release/file/1392446/download United States National Institute For Justice - Research on Body-Worn Cameras and Law Enforcement: (ref. 6) https://nij.ojp.gov/topics/articles/research-body-worn-cameras-and-law-enforcement Justia - Scott v. Harris, 550 U.S. 372 (2007): (ref. 7) https://supreme.justia.com/cases/federal/us/550/372/

If this legal argument was derived from reasonable deduction, then this is the legal argument that should have been presented during the FIRST United States Federal Ninth Circuit Court case on this Civil Rights issue. In Fact, 'De Facto', the United States Federal Ninth Circuit Court ruled the exact opposite as 'De Jure' case law: "material fact exists concerning whether [Police] interfered with Fordyce's First Amendment Right to gather news." - Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995) (ref. 2) In Fact, 'De Facto', the United States Supreme Court also ruled the exact opposite, as prior restraint is "the most serious and the least tolerable infringement on First Amendment Rights" - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 3, ref. 4) In the United States, once a 'De Jure' Federal case law on Civil Rights protected by Article 6, Clause 2 of the United States Constitution has been established, a Federal Ninth Circuit Judge becomes bound within the parameters of that Federal Ninth Circuit Court decision, and cannot detract from such Federal judicial rulings, without severely undermining their constitutional judicial peer integrity and making an unconstitutional ruling that is capable of being overturned by the appellate and supreme courts. In this instance, a U.S. Citizens First Amendment Right to gather news in a public space without prior restraint interference. And since the Federal Ninth Circuit Court did not establish a magical fifteen feet (15') distance, no such de jure or de facto distance exists, and any State or Federal legislature and/or State or Federal court that detracts from such established Federal Ninth Circuit Court case law parameters, would in fact be conducting prior restraint themselves. "Where Rights secured by the Constitution are involved, there can be no 'rule making' or legislation which would abrogate them." - Miranda v. Arizona, (384 U.S. 426, 491; 86 S. Ct. 1603) "The Constitution of these United States is the supreme law of the land. Any law that is repugnant to the Constitution is null and void of law." "void ab initio" - Marbury v. Madison, (5 US 137) Ninth Circuit (with jurisdiction over Alaska, Arizona, California, Guam, Hawaii, Idaho, Montana, Nevada, the Northern Mariana Islands, Oregon, and Washington). The United States Federal Ninth Circuit Court: "material fact exists concerning whether [Police] interfered with Fordyce's First Amendment Right to gather news." - Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995) (ref. 2) "Defendants [police officers] stopped Plaintiff only to get him to delete the pictures from his cell phone, and then arrested him only because of his repeated challenges to their authority. Such circumstances would make Plaintiff’s arrest an illegal retaliatory arrest and prior restraint." - Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013) (ref. 3) "there is a constitutional Right of the public to film the official activities of police officers in a public place." - Hawaii v. Russo (2017) - Supreme Court of Hawaii. (ref. 4) Arizona House Bill 2319 is specifically enforcing unconstitutional prior restraint penalties for the First Amendment exercise of free speech, journalism and press prior to publication. A prior restraint is an official government restriction of free speech, journalism and press prior to publication. Prior restraints are viewed by the United States Supreme Court as "the most serious and the least tolerable infringement on First Amendment Rights" - Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) (ref. 5, ref. 6) If passed, Arizona House Bill 2319 is expected to be struck down as "unconstitutional" in the United States Federal Ninth Circuit Court within 3 years. Reference: House Bill 2319 - anyone who police order to stop filming but continues to do so would face a class 3 misdemeanor and up to 30 days in jail: (ref. 1) https://www.azleg.gov/legtext/55leg/2R/bills/HB2319P.pdf Fordyce v. City of Seattle, 55 F.3d 436, 438 (9th Cir. 1995): (ref. 2) https://caselaw.findlaw.com/us-9th-circuit/1054985.html Adkins v. Limtiaco, No. 11-17543, 2013 WL 4046720 (9th Cir. Aug. 12, 2013): (ref. 3) https://www.govinfo.gov/content/pkg/USCOURTS-gud-1_09-cv-00029/pdf/USCOURTS-gud-1_09-cv-00029-2.pdf Hawaii v. Russo (2017) - Supreme Court of Hawaii: (ref. 4) https://cases.justia.com/hawaii/supreme-court/2017-scwc-14-0000986-0.pdf Nebraska Press Association v. Stuart, 427 U.S. 539 (1976) - United States Supreme Court (ref. 5) https://tile.loc.gov/storage-services/service/ll/usrep/usrep427/usrep427539/usrep427539.pdf Wikipedia - Prior restraint: (ref. 6) https://en.wikipedia.org/wiki/Prior_restraint

Any discussions and/or peer reviews about this specific topic thread? "I think of the horizon at midnight, the sky and sea blurring together." - Sophie Hardcastle Reference: Wikipedia - Schwarzschild metric - Flamm's paraboloid: (ref. 1) https://en.wikipedia.org/wiki/Schwarzschild_metric#Flamm's_paraboloid Wikipedia - Schwarzschild radius: (ref. 2) https://en.wikipedia.org/wiki/Schwarzschild_radius Wikipedia - Schwarzschild metric: (ref. 3) https://en.wikipedia.org/wiki/Schwarzschild_metric Wikipedia - Boyer-Lindquist coordinates - Line element: (ref. 4) https://en.wikipedia.org/wiki/Boyer-Lindquist_coordinates#Line_element Science Forums - General Relativity: Four Exterior Metric Solutions - Orion1: (ref. 5) https://www.scienceforums.net/topic/126549-general-relativity-four-exterior-metric-solutions/ Wikipedia - Photon sphere: (ref. 6) https://en.wikipedia.org/wiki/Photon_sphere Wikipedia - Astrophysical jet: (ref. 7) https://en.wikipedia.org/wiki/Astrophysical_jet Wikipedia - Accretion disk: (ref. 8) https://en.wikipedia.org/wiki/Accretion_disk Wikipedia - Black hole - Innermost stable circular orbit: (ref. 9) https://en.wikipedia.org/wiki/Black_hole#Innermost_stable_circular_orbit_(ISCO) Mathematica 7 - General Relativity - Flamm's Paraboloid source code notebook attachment: General Relativity - Flamm's Paraboloid.nb Mathematica 7 - General Relativity - Schwarzschild Black Hole Toy Model source code notebook attachment: General Relativity - Schwarzschild Black Hole Toy Model.nb Please merge the threads if there is a protocol violation.

Any discussions and/or peer reviews about this specific topic thread? "I think of the horizon at midnight, the sky and sea blurring together." - Sophie Hardcastle

[math]\text{General Relativity: Flamm's Paraboloid}[/math] [math]\text{The exterior Schwarzschild metric space-time curvature solutions for a radius greater than the Schwarzschild radius } (r > r_{s})[/math] [math]\text{can be visualized as mathematical parametrics. There is an additional Euclidean z-axis metric polar dimension w,}[/math] [math]\text{which has no physical reality and is not part of space-time.}[/math] [math]\color{blue}{ \text{Any discussions and/or peer reviews about this specific topic thread?}}[/math] [math]\color{blue}{\text{"I think of the horizon at midnight, the sky and sea blurring together." - Sophie Hardcastle}}[/math]