Orion1

Planck satellite baryonic cosmological composition parameter: (ref. 1, pg. 11, ref. 2, pg. 3) [math]\Omega_{b} = 0.0495[/math] [math]\;[/math] Black holes cosmological composition parameter: {ref. 2, pg. 3) [math]\Omega_{bh} = 0.00007[/math] [math]\;[/math] Solar mass: (ref. 3) [math]M_{\odot} = 1.9885 \cdot 10^{30} \; \text{kg}[/math] [math]\;[/math] Milky Way galaxy mass: (ref. 4, pg. 1) [math]M_{mw} = 1.260 \cdot 10^{12} \cdot M_{\odot} = 2.506 \cdot 10^{42} \; \text{kg}[/math] [math]\boxed{M_{mw} = 2.506 \cdot 10^{42} \; \text{kg}}[/math] [math]\;[/math] PSR J2215+5135 pulsar Tolman-Oppenheimer-Volkoff observational lower mass limit: (ref. 5) [math]\boxed{M_{bh} \geq 2.27 \cdot M_{\odot}}[/math] [math]\boxed{M_{bh} \geq 4.514 \cdot 10^{30} \; \text{kg}}[/math] [math]\;[/math] Stellar class O upper mass limit: (ref. 6) [math]\boxed{M_{bh} \geq 16 \cdot M_{\odot}}[/math] [math]\boxed{M_{bh} \geq 3.182 \cdot 10^{31} \; \text{kg}}[/math] [math]\;[/math] Toy model black holes per galaxy average number: [math]\frac{N_{bh}}{N_g} = \frac{\Omega_{bh} M_{mw}}{\Omega_b M_{bh}} = \left(1.114 \cdot 10^{8} \rightarrow 7.851 \cdot 10^{8} \right) \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\boxed{\frac{N_{bh}}{N_g} = \frac{\Omega_{bh} M_{mw}}{\Omega_b M_{bh}}}[/math] [math]\boxed{\frac{N_{bh}}{N_g} = \left(1.114 \cdot 10^{8} \rightarrow 7.851 \cdot 10^{8} \right) \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\;[/math] Synthetic catalog black holes per galaxy average number: (ref. 7, pg. 1) [math]\frac{N_{bh}}{N_g} = 1.693 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Planck 2013 results. XVI. Cosmological parameters: (ref. 1) http://planck.caltech.edu/pub/2013results/Planck_2013_results_16.pdf The Cosmic Energy Inventory: (ref. 2) http://arxiv.org/pdf/astro-ph/0406095v2.pdf Wikipedia - Sun Sol: (ref. 3) https://en.wikipedia.org/wiki/Sun Mass models of the Milky Way: (ref. 4) http://arxiv.org/pdf/1102.4340v1 Wikipedia - Tolman-Oppenheimer-Volkoff limit: (ref. 5) https://en.wikipedia.org/wiki/Tolman-Oppenheimer-Volkoff_limit Wikipedia - Stellar classification - Harvard spectral classification: (ref. 6) https://en.wikipedia.org/wiki/Stellar_classification#Harvard_spectral_classification Synthetic catalog of black holes in the Milky Way: (ref. 7) https://arxiv.org/pdf/1908.08775.pdf

Affirmative, I seem to have reached a reference citation impasse regarding the tensor field functions integration of [math]\Lambda^{\mu}_{\alpha}[/math] and [math]\Lambda^{\nu}_{\beta}[/math]. All of the references that have been cited do not demonstrate a functions integration past this initial point for a tensor field. Is this approach at least mathematically and symbolically correct to this point? Any citations or recommendations? Any discussions and/or peer reviews about this specific topic thread?

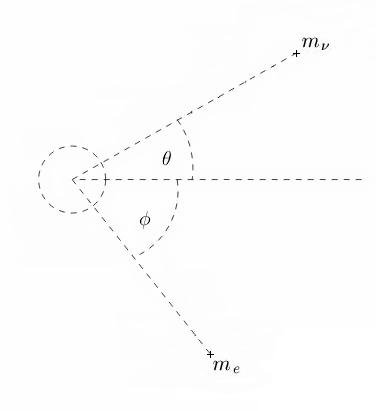
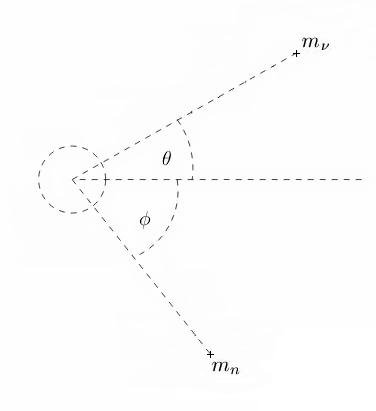
Affirmative, revision complete. Derivation of neutrino mass from neutrino scattering: [math]\;[/math] [math]\theta[/math] - scattered neutrino angle [math]\phi[/math] - electron recoil angle [math]E_{\nu i}[/math] - initial neutrino total energy [math]E_{\nu f}[/math] - final neutrino total energy [math]E_{e}[/math] - electron total energy [math]E_{\nu}[/math] - neutrino total energy Scattered particles rebounding with relativistic momentum have total energy: [math]E_{e} = \gamma_{e} m_{e} c^{2} \; \; \; \; \; \; E_{\nu} = \gamma_{\nu} m_{\nu} c^{2}[/math] Where [math]m_{e}[/math] and [math]m_{\nu}[/math] are the particle rest masses. [math]\gamma_{e}[/math] and [math]\gamma_{\nu}[/math] are the Lorentz factors. (ref. 1) [math]\;[/math] Observational measurements of both particle total energy and velocity, it is possible to calculate the particle rest masses [math]m_{e}[/math] and [math]m_{\nu}[/math]: [math]\boxed{m_{e} = \frac{E_{e}}{\gamma_{e} c^{2}}} \; \; \; \; \; \; \boxed{m_{\nu} = \frac{E_{\nu}}{\gamma_{\nu} c^{2}}} \tag{0}[/math] [math]\;[/math] [math]E_{e} \sin \phi = E_{\nu f} \sin \theta \tag{1}[/math] [math]\;[/math] [math]E_{e} \cos \phi + E_{\nu f} \cos \theta = E_{\nu i} \tag{2}[/math] [math]\;[/math] Isolate [math]E_{e} \cos \phi[/math] from equation (2): [math]E_{e} \cos \phi = E_{\nu i} - E_{\nu f} \cos \theta \tag{3}[/math] [math]\;[/math] Divide equation (1) by equation (3) for an expression for [math]\tan \phi[/math]. [math]\;[/math] [math]\tan \phi = \frac{E_{\nu f} \sin \theta}{E_{\nu i} - E_{\nu f} \cos \theta} = \frac{\sin \theta}{\frac{E_{\nu i}}{E_{\nu f}} - \cos \theta} \tag{4}[/math] [math]\;[/math] Acquire a substitution for [math]\frac{E_{\nu i}}{E_{\nu f}}[/math] to eliminate [math]E_{\nu f}[/math]. Use the Compton equation, which can be rearranged to yield [math]\frac{\lambda_{\nu f}}{\lambda_{\nu i}} = \frac{E_{\nu i}}{E_{\nu f}}[/math] in terms of [math]\lambda_{\nu i}[/math] alone. [math]\;[/math] [math]\frac{\lambda_{\nu f}}{\lambda_{\nu i}} = \frac{E_{\nu i}}{E_{\nu f}} \tag{5}[/math] [math]\;[/math] [math]\frac{\lambda_{\nu f}}{\lambda_{\nu i}} = \frac{E_{\nu i}}{E_{\nu f}} = 1 + \frac{E_{\nu i}}{E_{e}} \left(1 - \cos \theta \right) = 1 + \frac{\gamma_{\nu} m_{\nu} c^2}{\gamma_{e} m_{e} c^2} \left(1 - \cos \theta \right) = 1 + \frac{\gamma_{\nu} m_{\nu}}{\gamma_{e} m_{e}} \left(1 - \cos \theta \right) \tag{6}[/math] [math]\;[/math] Substituting equation (6) into equation (4) and eliminate [math]E_{\nu i}[/math] and [math]E_{\nu f}[/math] in favor of [math]m_{\nu}[/math] alone. [math]\tan \phi = \frac{\sin \theta}{\frac{E_{\nu i}}{E_{\nu f}} - \cos \theta} = \frac{\sin \theta}{1 + \frac{\gamma_{\nu} m_{\nu}}{\gamma_{e} m_{e}} \left(1 - \cos \theta \right) - \cos \theta} = \frac{\sin \theta}{\left(1 + \frac{\gamma_{\nu} m_{\nu}}{\gamma_{e} m_{e}} \right)\left(1 - \cos \theta \right)} \tag{7}[/math] [math]\;[/math] Utilizing a trigonometric identity produces the desired result, specifically: [math]\frac{1 - \cos \theta}{\sin \theta} = \tan \left(\frac{\theta}{2} \right) \tag{8}[/math] [math]\;[/math] Substituting this trigonometric identity into equation (7) results in: [math]\left(1 + \frac{\gamma_{\nu} m_{\nu}}{\gamma_{e} m_{e}} \right) \tan \phi = \cot \frac{\theta}{2} \tag{9}[/math] [math]\;[/math] Solve for neutrino rest mass [math]m_{\nu}[/math]: [math]\tan \phi + \frac{\gamma_{\nu} m_{\nu}}{\gamma_{e} m_{e}} \tan \phi = \cot \frac{\theta}{2} \tag{10}[/math] [math]\;[/math] [math]\frac{\gamma_{\nu} m_{\nu}}{\gamma_{e} m_{e}} \tan \phi = \left(\cot \frac{\theta}{2} - \tan \phi \right) \tag{11}[/math] [math]\;[/math] Electron-neutrino scattering neutrino rest mass: [math]\boxed{m_{\nu} = \frac{\gamma_{e} m_{e} \cot \phi}{\gamma_{\nu}} \left(\cot \frac{\theta}{2} - \tan \phi \right)} \tag{12}[/math] [math]\;[/math] Nuclear-neutrino scattering neutrino rest mass: [math]\boxed{m_{\nu} = \frac{\gamma_{n} m_{n} \cot \phi}{\gamma_{\nu}} \left(\cot \frac{\theta}{2} - \tan \phi \right)} \tag{13}[/math] [math]m_{n}[/math] - nuclear rest mass [math]\;[/math] Electron interaction neutrino scattering angle [math]\theta[/math]: [math]\boxed{\theta = 2 \operatorname{arccot} \left(\frac{\left(\gamma_{e} m_{e} + \gamma_{\nu} m_{\nu} \right) \tan \phi}{\gamma_{e} m_{e}} \right)} \tag{14}[/math] [math]\;[/math] Neutrino interaction electron recoil angle [math]\phi[/math]: [math]\boxed{\phi = \arctan \left(\frac{\gamma_{e} m_{e} \cot \frac{\theta}{2}}{\gamma_{e} m_{e} + \gamma_{\nu} m_{\nu}} \right)} \tag{15}[/math] [math]\;[/math] Nuclear interaction neutrino scattering angle [math]\theta[/math]: [math]\boxed{\theta = 2 \operatorname{arccot} \left(\frac{\left(\gamma_{n} m_{n} + \gamma_{\nu} m_{\nu} \right) \tan \phi}{\gamma_{n} m_{n}} \right)} \tag{16}[/math] [math]\;[/math] Neutrino interaction nuclear recoil angle [math]\phi[/math]: [math]\boxed{\phi = \arctan \left(\frac{\gamma_{n} m_{n} \cot \frac{\theta}{2}}{\gamma_{n} m_{n} + \gamma_{\nu} m_{\nu}} \right)} \tag{17}[/math] [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Lorentz factor: (ref. 1) https://en.wikipedia.org/wiki/Lorentz_factor Wikipedia - Compton scattering - Derivation of the scattering formula: https://en.wikipedia.org/wiki/Compton_scattering#Derivation_of_the_scattering_formula Physics 253 - Compton Scattering - Patrick LeClair http://pleclair.ua.edu//PH253/Notes/compton.pdf Orion1 - Neutrino mass from Fermi-Dirac statistics...: https://www.scienceforums.net/topic/90189-neutrino-mass-from-fermi-dirac-statistics/ Science News - Neutrinos seen scattering off an atom’s nucleus for the first time: https://www.sciencenews.org/article/neutrinos-seen-scattering-atoms-nucleus-first-time

De Broglie relativistic momentum: (ref. 1) [math]p = \frac{\hbar}{\overline{\lambda}} = \gamma m_0 v[/math] [math]\;[/math] Relativistic energy-momentum relation and relativistic mass particle total energy identity: [math]\boxed{E_{t} = \sqrt{\left(m_{0} c^{2} \right)^{2} + \left(pc \right)^{2}} = \gamma m_0 c^2}[/math] [math]\;[/math] [math]\boxed{E_{t} = \sqrt{\left(m_{0} c^{2} \right)^{2} + \left(\frac{\hbar c}{\overline{\lambda}} \right)^{2}} = \gamma m_0 c^2}[/math] [math]\;[/math] Is this equation an identity for a relativistic mass particle? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Matter wave: (ref. 1) https://en.wikipedia.org/wiki/Matter_wave

Relativistic energy-momentum relation total energy: (ref. 1) [math]E_{t}^{2} = \left(m_{0} c^{2} \right)^{2} + \left(pc \right)^{2} [/math] [math]E_{t} = \sqrt{\left(m_{0} c^{2} \right)^{2} + \left(pc \right)^{2}}[/math] [math]\;[/math] Relativistic mass particle total energy: (ref. 2) [math]E_{t} = \gamma m_0 c^{2}[/math] [math]\;[/math] Relativistic energy-momentum relation and relativistic mass particle total energy identity: [math]\boxed{E_{t} = \sqrt{\left(m_{0}c^{2} \right)^{2} + \left(pc \right)^{2}} = \gamma m_0 c^2}[/math] [math]\;[/math] Is this equation an identity for a relativistic mass particle? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Energy-momentum relation: (ref. 1) https://en.wikipedia.org/wiki/Energy–momentum_relation#Special_relativity Wikipedia - Energy-momentum relation - heuristic approach for massive particles: (ref. 2) https://en.wikipedia.org/wiki/Energy–momentum_relation#Heuristic_approach_for_massive_particle

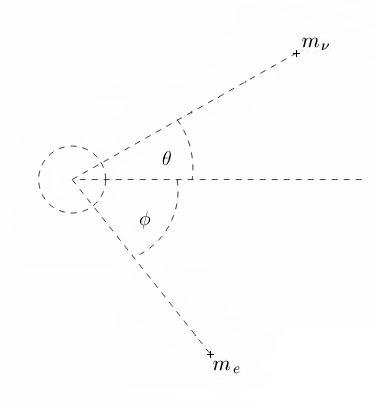
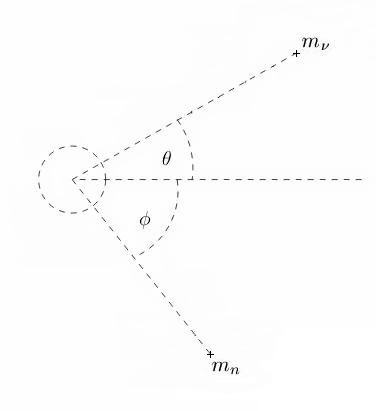
Derivation of neutrino mass from neutrino scattering: [math]\;[/math] [math]\theta[/math] - scattered neutrino angle [math]\phi[/math] - electron recoil angle [math]p_{i}[/math] - initial neutrino momentum [math]p_{f}[/math] - final neutrino momentum [math]p_{e}[/math] - electron momentum [math]\;[/math] Scattered particles rebounding with relativistic momentum have total energy: [math]E_{e} = \gamma m_{0e} c^{2} = m_{e} c^{2} \; \; \; \; \; \; E_{\nu} = \gamma m_{0\nu} c^{2} = m_{\nu} c^{2}[/math] Where [math]m_{e}[/math] and [math]m_{\nu}[/math] are the relativistic particle masses. [math]\;[/math] Observational measurements of both particle total energy and velocity, it is possible to calculate the rest particle masses [math]m_{0e}[/math] and [math]m_{0\nu}[/math]: [math]\boxed{m_{0e} = \frac{E_{e}}{\gamma c^{2}}} \; \; \; \; \; \; \boxed{m_{0\nu} = \frac{E_{\nu}}{\gamma c^{2}}} \tag{0}[/math] [math]\;[/math] [math]p_{e} \sin \phi = p_{f} \sin \theta \tag{1}[/math] [math]\;[/math] [math]p_{e} \cos \phi + p_{f} \cos \theta = p_{i} \tag{2}[/math] [math]\;[/math] Isolate [math]p_{e} \cos \phi[/math] from equation [math](2)[/math]: [math]p_{e} \cos \phi = p_{i} - p_{f} \cos \theta \tag{3}[/math] [math]\;[/math] Divide equation [math](1)[/math] by equation [math](3)[/math] for an expression for [math](3)[/math] for an expression for [math]\tan \phi[/math]: [math]\;[/math] [math]\tan \phi = \frac{p_{f} \sin \theta}{p_{i} - p_{f} \cos \theta} = \frac{\sin \theta}{\frac{p_{i}}{p_{f}} - \cos \theta} \tag{4}[/math] [math]\;[/math] Acquire a substitution for [math]\frac{p_{i}}{p_{f}}[/math] to eliminate [math]p_{f}[/math]. Use the Compton equation, which can be rearranged to yield [math]\frac{\lambda_{f}}{\lambda_{i}} = \frac{p_{i}}{p_{f}}[/math] in terms of [math]\lambda_{i}[/math] alone. [math]\;[/math] [math]\frac{\lambda_{f}}{\lambda_{i}} = \frac{p_{i}}{p_{f}} \tag{5}[/math] [math]\;[/math] [math]\frac{\lambda_{f}}{\lambda_{i}} = \frac{p_{i}}{p_{f}} = 1 + \frac{E_{\nu}}{E_{e}} \left(1 - \cos \theta \right) = 1 + \frac{m_{\nu} c^2}{m_{e} c^2} \left(1 - \cos \theta \right) = 1 + \frac{m_{\nu}}{m_{e}} \left(1 - \cos \theta \right) \tag{6}[/math] [math]\;[/math] Substituting equation [math](6)[/math] into equation [math](4)[/math], and eliminate [math]p_{i}[/math] and [math]p_{f}[/math] in favor of [math]m_{\nu}[/math] alone. [math]\;[/math] [math]\tan \phi = \frac{\sin \theta}{\frac{p_{i}}{p_{f}} - \cos \theta} = \frac{\sin \theta}{1 + \frac{m_{\nu}}{m_{e}} \left(1 - \cos \theta \right) - \cos \theta} = \frac{\sin \theta}{\left(1 + \frac{m_{\nu}}{m_{e}} \right)\left(1 - \cos \theta \right)} \tag{7}[/math] [math]\;[/math] Utilizing a trigonometric identity produces the desired result, specifically: [math]\frac{1 - \cos \theta}{\sin \theta} = \tan \left(\frac{\theta}{2} \right) \tag{8}[/math] [math]\;[/math] Substituting this trigonometric identity into equation [math](7)[/math] results in: [math]\left(1 + \frac{m_{\nu}}{m_{e}} \right) \tan \phi = \cot \frac{\theta}{2} \tag{9}[/math] [math]\;[/math] Solve for neutrino mass [math]m_{\nu}[/math]: [math]\tan \phi + \frac{m_{\nu}}{m_{e}} \tan \phi = \cot \frac{\theta}{2} \tag{10}[/math] [math]\;[/math] [math]\frac{m_{\nu}}{m_{e}} \tan \phi = \left(\cot \frac{\theta}{2} - \tan \phi \right) \tag{11}[/math] [math]\;[/math] Electron-neutrino scattering neutrino mass: [math]\boxed{m_{\nu} = m_{e} \cot \phi \left(\cot \frac{\theta}{2} - \tan \phi \right)} \tag{12}[/math] [math]\;[/math] Nuclear-neutrino scattering neutrino mass: [math]\boxed{m_{\nu} = m_{n} \cot \phi \left(\cot \frac{\theta}{2} - \tan \phi \right)} \tag{13}[/math] [math]\;[/math] [math]m_{n}[/math] - nuclear mass [math]\;[/math] Electron interaction neutrino scattering angle [math]\theta[/math]: [math]\boxed{\theta = 2 \operatorname{arccot} \left(\frac{\left(m_{e} + m_{\nu} \right) \tan \phi}{m_{e}} \right)} \tag{14}[/math] [math]\;[/math] Neutrino interaction electron recoil angle [math]\phi[/math]: [math]\boxed{\phi = \arctan \left(\frac{m_{e} \cot \frac{\theta}{2}}{m_{e} + m_{\nu}} \right)} \tag{15}[/math] [math]\;[/math] Nuclear interaction neutrino scattering angle [math]\theta[/math]: [math]\boxed{\theta = 2 \operatorname{arccot} \left(\frac{\left(m_{n} + m_{\nu} \right) \tan \phi}{m_{n}} \right)} \tag{16}[/math] [math]\;[/math] Neutrino interaction nuclear recoil angle [math]\phi[/math]: [math]\boxed{\phi = \arctan \left(\frac{m_{n} \cot \frac{\theta}{2}}{m_{n} + m_{\nu}} \right)} \tag{17}[/math] [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Compton scattering - Derivation of the scattering formula: https://en.wikipedia.org/wiki/Compton_scattering#Derivation_of_the_scattering_formula Physics 253 - Compton Scattering - Patrick LeClair http://pleclair.ua.edu//PH253/Notes/compton.pdf Orion1 - Neutrino mass from Fermi-Dirac statistics...: https://www.scienceforums.net/topic/90189-neutrino-mass-from-fermi-dirac-statistics/ Science News - Neutrinos seen scattering off an atom’s nucleus for the first time: https://www.sciencenews.org/article/neutrinos-seen-scattering-atoms-nucleus-first-time

Please cite which Wikipedia reference? Also, I am not certain which 'discussion' with 'list of references' that is being inferred, please clarify. (ref. 7) Server guideline rule Section 2 (7) prohibits me from directing discussion to another server. My apology if my stringent interpretation of this rule is overtly strict or interpreted as a deflection or deferment, please clarify. (ref. 7) Do you agree with this equation for deriving a relativistic lagrangian? Relativistic Lagrangian integration via substitution: [math]\mathcal{L} = \sum_{1}^{n} E_{k}\left(n \right) - \sum_{1}^{n} E_{p}\left(n \right) = \sum_{1}^{n} \mathcal{L}\left(n \right) = 0[/math] Relativistic Lagrangian: [math]\boxed{\mathcal{L} = \sum_{1}^{n} \mathcal{L}\left(n \right) = 0}[/math] Affirmative, revision complete. [math]\;[/math] Einstein's field equations: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = \frac{8 \pi G}{c^{4}} T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations in natural units: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = 8 \pi T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations Ricci tensor in natural units: [math]\boxed{ R_{\mu \nu} = 8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}[/math] [math]\;[/math] Lagrangian equation: [math]\mathcal{L} = \underbrace{ \mathbb{R} }_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0[/math] [math]\;[/math] General relativity Lagrangian equation: [math]\boxed{\mathcal{L} = \underbrace{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] A massless gravitational wave is still massless on a Planck scale, and the result is still a metric tensor field. [math]\;[/math] Metric tensor field: (ref. 1, pg. 21, eq. 1.68) [math]T^{' \mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] The general relativity Ricci tensor is a metric tensor field: [math]\boxed{R_{\mu \nu} = T^{' \mu \nu} \left(x' \right)}[/math] [math]\;[/math] Lagrangian equation for a massless Planck graviton: [math]\boxed{\mathcal{L} = \underbrace{ \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right) }_{QG} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] General relativity and Planck quantum gravity identity: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric: (ref. 2) [math]g_{\mu \nu} = \eta_{\mu \nu} + h_{\mu \nu}[/math] [math]\;[/math] [math]\eta_{\mu \nu}[/math] - perturbed nondynamical background metric [math]h_{\mu \nu}[/math] - true metric deviation of [math]g_{\mu \nu}[/math] from flat spacetime [math]\;[/math] [math]h_{\mu \nu}[/math] must be negligible compared to [math]\eta_{\mu \nu}[/math]: [math]|h_{\mu \nu}| \ll 1[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 1: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R \left(\eta_{\mu \nu} + h_{\mu \nu} \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 2: [math]\boxed{8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) - \frac{1}{2} R \left(\eta_{\mu \nu} + h_{\mu \nu} \right)}[/math] [math]\;[/math] General relativity Ricci scalar curvature: (ref. 3, ref. 4) [math]R = g^{\mu \nu } R_{\mu \nu}[/math] [math]\;[/math] General relativity Ricci scalar curvature and Planck quantum gravity scalar curvature: [math]R = g^{\mu \nu } R_{\mu \nu} = g^{\mu \nu } \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)[/math] [math]\boxed{R = g^{\mu \nu } \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 2 integration via substitution: [math]8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) - \frac{1}{2} g^{\mu \nu} \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(\eta_{\mu \nu} + h_{\mu \nu} \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} g^{\mu \nu}\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 3: [math]\boxed{8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} g^{\mu \nu}\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime inverse metric: (ref. 2) [math]g^{\mu \nu} = \eta^{\mu \nu} - h^{\mu \nu}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 4: [math]\boxed{8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} \left(\eta^{\mu \nu} - h^{\mu \nu} \right)\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] [math]\Lambda^{\mu}_{\alpha} = \frac{\partial \xi^{\mu}}{\partial x^{\alpha}} \; \; \; \; \; \; \Lambda^{\nu}_{\beta} = \frac{\partial \xi^{\nu}}{\partial x^{\beta}}[/math] [math]\;[/math] [math]x^{\alpha} = \left(ct, r, \theta, \phi \right) \; \; \; \; \; \; x^{\beta} = \left(ct, r, \theta, \phi \right)[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 5: (ref. 5) [math]\boxed{8 \pi T_{\mu \nu} = \left(\frac{\partial \xi^{\mu}}{\partial x^{\alpha}} \right)\left(\frac{\partial \xi^{\nu}}{\partial x^{\beta}} \right) T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} \left(\eta^{\mu \nu} - h^{\mu \nu} \right)\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] General relativity stress-energy tensor: [math]T_{\mu \nu} = \pm \left(\begin{matrix} -\rho & 0 & 0 & 0 \\ 0 & p & 0 & 0 \\ 0 & 0 & p & 0 \\ 0 & 0 & 0 & p \end{matrix} \right)[/math] [math]\;[/math] In spherical coordinates [math](ct, r, \theta, \phi)[/math] the Minkowski flat spacetime metric takes the form: [math]ds^{2} = -c^{2} dt^{2} + dr^{2} + r^{2} d\theta^{2} + r^{2} \sin^{2} \theta \; d\phi^{2}[/math] [math]\;[/math] General relativity Minkowski flat spacetime metric tensor: [math]T^{\alpha \beta} \left(x \right) = \pm \begin{pmatrix} -c^{2} dt^{2} & 0 & 0 & 0 \\ 0 & dr^{2} & 0 & 0 \\ 0 & 0 & r^{2} d\theta^{2} & 0 \\ 0 & 0 & 0 & r^{2} \sin^{2} \theta \; d\phi^{2} \end{pmatrix}[/math] [math]\;[/math] General relativity Minkowski flat spacetime metric: [math]\eta_{\mu \nu} = \pm \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}[/math] [math]\;[/math] General relativity Minkowski flat spacetime metric is equivalent to the inverse metric: (ref. 6) [math]\boxed{\eta_{\mu \nu} = \eta^{\mu \nu}}[/math] [math]\;[/math] General relativity Minkowski flat spacetime perturbed nondynamical background metric deviation is equivalent to the inverse metric deviation: [math]\boxed{h_{\mu \nu} = h^{\mu \nu}}[/math] [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf Wikipeda - General relativity - linearized gravity: (ref. 2) https://en.wikipedia.org/wiki/Linearized_gravity Wikipeda - General relativity: (ref. 3) https://en.wikipedia.org/wiki/General_relativity#Einstein's_equations Wikipeda - General relativity: (ref. 4) https://en.wikipedia.org/wiki/Metric_tensor_(general_relativity)#Einstein's_equations Wikipeda - General relativity - Metric tensor - Local coordinates and matrix representations: (ref. 5) https://en.wikipedia.org/wiki/Metric_tensor_(general_relativity)#Local_coordinates_and_matrix_representations Wikipeda - Lorentz covariance: (ref. 6) https://en.wikipedia.org/wiki/Lorentz_covariance Science Forums - Guidelines: (ref. 7) https://www.scienceforums.net/guidelines/

Affirmative, is this an identity of the lagrangian Dirac equation with EM interaction? [math]\mathcal{L} = \underbrace{\overline{\psi} \left(i \gamma^{\mu} D_{\mu} - m \right) \psi}_{Dirac} - \underbrace{e \overline{\psi} \gamma^{\mu} Q \psi A_{\mu}}_{EM \text{ } interaction}[/math] [math]\;[/math] [math]\mathcal{L} = \overline{\psi} \left(i \gamma^{\mu} D_{\mu} - m \right) \psi - e \overline{\psi} \gamma^{\mu} Q \psi A_{\mu}[/math] [math]\;[/math] [math]\mathcal{L} = \overline{\psi} i \gamma^{\mu} D_{\mu} \psi - \overline{\psi} m \psi - e \overline{\psi} \gamma^{\mu} Q \psi A_{\mu}[/math] [math]\;[/math] [math]\mathcal{L} = \overline{\psi} i \gamma^{\mu} D_{\mu} \psi - e \overline{\psi} \gamma^{\mu} Q \psi A_{\mu} - \overline{\psi} m \psi[/math] [math]\;[/math] [math]\mathcal{L} = \overline{\psi} \gamma^{\mu} \left(i D_{\mu} - e Q A_{\mu} \right)\psi - \overline{\psi} m \psi[/math] [math]\;[/math] [math]\boxed{\mathcal{L} = \overline{\psi} \left[\gamma^{\mu}\left(i D_{\mu} - e Q A_{\mu} \right) - m \right] \psi}[/math]

The scientific author of the original lagrangian equation appears to be modeling a massless and chargeless quantum field interaction. [math]\;[/math] General relativity Lagrangian equation with mass and charge and a GUT quaternion: (ref. 1, ref. 2, pg. 8, eq. 2.8) [math]\boxed{\mathcal{L} = \underbrace{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{\overline{\psi} \left(i \gamma^{\mu} D_{\mu} - m \right) \psi}_{Dirac} - \underbrace{e \overline{\psi} \gamma^{\mu} Q \psi A_{\mu}}_{EM \text{ } interaction} + \underbrace{|D_{\mu} h|^2 - V\left(|h| \right)}_{Higgs} + \underbrace{\overline{\psi^{\alpha}} \gamma_{\mu} \left(A_{\mu}^{\alpha \beta} \psi^{\beta} + \psi^{\alpha} B_{\mu} \right)}_{GUT \text{ } quaternion} = 0}[/math] [math]\;[/math] Reference: Wikipedia - Grand Unified Theory - Symplectic groups and quaternion representations: (ref. 1) https://en.wikipedia.org/wiki/Grand_Unified_Theory#Symplectic_groups_and_quaternion_representations Search For The Standard Model Higgs Boson In Leptons Plus Jets Final States: (ref. 2) https://www-d0.fnal.gov/results/publications_talks/thesis/nguyen/thesis.pdf

There does not appear to be a scientific consensus for the lagrangian equation for GUT Pati-Salam models. The integration strategy appears to involve modeling both gauge symmetry and particle hierarchy into the Yukawa lagrangian. [math]\;[/math] Yukawa lagrangian: [math]\mathcal{L} = \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0[/math] [math]\;[/math] However, the GUT quaternion lagrangian equation appears to exhibit both gauge symmety and particle heirarchy and matrix parameters which could be compatible with the SO(10) regime under Pati-Salam. [math]\;[/math] GUT quaternion lagrangian equation: (ref. 1) [math]\mathcal{L} = \overline{\psi^{a}} \gamma_{\mu} \left(A_{\mu}^{ab} \psi^{b} + \psi^{a} B_{\mu} \right)[/math] [math]\;[/math] Because the GUT energy scale is well below the Planck energy scale, the general relativity Lagrangian equation may still be utilized without the introduction of a graviton. [math]\;[/math] GUT energy scale: [math]\Lambda_{\text{GUT}} \approx 10^{16} \; \text{GeV}[/math] [math]\;[/math] Planck energy scale: [math]E_{P} = 1.221 \cdot 10^{19} \; \mathrm {GeV}[/math] [math]\;[/math] General relativity Lagrangian equation with a GUT quaternion: [math]\boxed{\mathcal{L} = \underbrace{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{\overline{\psi^{a}} \gamma_{\mu} \left(A_{\mu}^{ab} \psi^{b} + \psi^{a} B_{\mu} \right)}_{\text{GUT quaternion}} = 0}[/math] Reference: Wikipedia - Grand Unified Theory - Symplectic groups and quaternion representations: (ref. 1) https://en.wikipedia.org/wiki/Grand_Unified_Theory#Symplectic_groups_and_quaternion_representations

Affirmative, revision complete. [math]\;[/math] Einstein's field equations: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = \frac{8 \pi G}{c^{4}} T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations in natural units: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = 8 \pi T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations Ricci tensor in natural units: [math]\boxed{ R_{\mu \nu} = 8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}[/math] [math]\;[/math] Lagrangian equation: [math]\mathcal{L} = \underbrace{ \mathbb{R} }_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0[/math] [math]\;[/math] General relativity Lagrangian equation: [math]\boxed{\mathcal{L} = \underbrace{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] A massless gravitational wave is still massless on a Planck scale, and the result is still a metric tensor field. [math]\;[/math] Metric tensor field: (ref. 1, pg. 21, eq. 1.68) [math]T^{' \mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] The general relativity Ricci tensor is a metric tensor field: [math]\boxed{R_{\mu \nu} = T^{' \mu \nu} \left(x' \right)}[/math] [math]\;[/math] Lagrangian equation for a massless Planck graviton: [math]\boxed{\mathcal{L} = \underbrace{ \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right) }_{QG} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] General relativity and Planck quantum gravity identity: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric: (ref. 2) [math]g_{\mu \nu} = \eta_{\mu \nu} + h_{\mu \nu}[/math] [math]\;[/math] [math]\eta_{\mu \nu}[/math] - perturbed non-dynamical background metric [math]h_{\mu \nu}[/math] - true metric deviation of [math]g_{\mu \nu}[/math] from flat spacetime [math]\;[/math] [math]h_{\mu \nu}[/math] must be negligible compared to [math]\eta_{\mu \nu}[/math]: [math]|h_{\mu \nu}| \ll 1[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 1: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R \left(\eta_{\mu \nu} + h_{\mu \nu} \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 2: [math]\boxed{8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) - \frac{1}{2} R \left(\eta_{\mu \nu} + h_{\mu \nu} \right)}[/math] [math]\;[/math] General relativity curvature scalar: (ref. 3) [math]R = g^{\mu \nu } R_{\mu \nu}[/math] [math]\;[/math] General relativity and Planck quantum gravity curvature scalar: [math]R = g^{\mu \nu } R_{\mu \nu} = g^{\mu \nu } \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)[/math] [math]\boxed{R = g^{\mu \nu } \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 2 integration via substitution: [math]8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) - \frac{1}{2} g^{\mu \nu} \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(\eta_{\mu \nu} + h_{\mu \nu} \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} g^{\mu \nu}\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 3: [math]\boxed{8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} g^{\mu \nu}\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime inverse metric: (ref. 2) [math]g^{\mu \nu} = \eta^{\mu \nu} - h^{\mu \nu}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 4: [math]\boxed{8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} \left(\eta^{\mu \nu} - h^{\mu \nu} \right)\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] [math]\Lambda^{\mu}_{\alpha} = \frac{\partial \xi^{\mu}}{\partial x^{\alpha}} \; \; \; \; \; \; \Lambda^{\nu}_{\beta} = \frac{\partial \xi^{\nu}}{\partial x^{\beta}}[/math] [math]\;[/math] [math]x^{\alpha} = \left(ct, r, \theta, \phi \right) \; \; \; \; \; \; x^{\beta} = \left(ct, r, \theta, \phi \right)[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 5: [math]\boxed{8 \pi T_{\mu \nu} = \left(\frac{\partial \xi^{\mu}}{\partial x^{\alpha}} \right)\left(\frac{\partial \xi^{\nu}}{\partial x^{\beta}} \right) T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} \left(\eta^{\mu \nu} - h^{\mu \nu} \right)\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] General relativity stress-energy tensor: [math]T_{\mu \nu} = \pm \left(\begin{matrix} -\rho & 0 & 0 & 0 \\ 0 & p & 0 & 0 \\ 0 & 0 & p & 0 \\ 0 & 0 & 0 & p \end{matrix} \right)[/math] [math]\;[/math] In spherical coordinates [math](ct, r, \theta, \phi)[/math] the Minkowski flat spacetime metric takes the form: [math]ds^{2} = -c^{2} dt^{2} + dr^{2} + r^{2} d\theta^{2} + r^{2} \sin^{2} \theta \; d\phi^{2}[/math] [math]\;[/math] General relativity Minkowski flat spacetime metric tensor: [math]T^{\alpha \beta} \left(x \right) = \pm \begin{pmatrix} -c^{2} dt^{2} & 0 & 0 & 0 \\ 0 & dr^{2} & 0 & 0 \\ 0 & 0 & r^{2} d\theta^{2} & 0 \\ 0 & 0 & 0 & r^{2} d\phi^{2} \end{pmatrix}[/math] [math]\;[/math] General relativity Minkowski flat spacetime metric: [math]\eta_{\mu \nu} = \pm \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}[/math] [math]\;[/math] General relativity Minkowski flat spacetime metric is equivalent to the inverse metric: [math]\boxed{\eta_{\mu \nu} = \eta^{\mu \nu}} \left(ref. 4 \right)[/math] [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf Wikipeda - General relativity - linearized gravity: (ref. 2) https://en.wikipedia.org/wiki/Linearized_gravity Wikipeda - General relativity: (ref. 3) https://en.wikipedia.org/wiki/General_relativity Wikipeda - Lorentz covariance: (ref. 4) https://en.wikipedia.org/wiki/Lorentz_covariance

Affirmative, revision complete. [math]\;[/math] Einstein's field equations: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = \frac{8 \pi G}{c^{4}} T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations in natural units: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = 8 \pi T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations Ricci tensor in natural units: [math]\boxed{ R_{\mu \nu} = 8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}[/math] [math]\;[/math] Lagrangian equation: [math]\mathcal{L} = \underbrace{ \mathbb{R} }_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0[/math] [math]\;[/math] General relativity Lagrangian equation: [math]\boxed{\mathcal{L} = \underbrace{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] A massless gravitational wave is still massless on a Planck scale, and the result is still a tensor field. [math]\;[/math] Tensor field: (ref. 1,pg. 21, eq. 1.68) [math]T^{' \mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] The general relativity Ricci tensor is a tensor field: [math]\boxed{R_{\mu \nu} = T^{' \mu \nu} \left(x' \right)}[/math] [math]\;[/math] Lagrangian equation for a massless Planck graviton: [math]\boxed{\mathcal{L} = \underbrace{ \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right) }_{QG} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] General relativity and Planck quantum gravity identity: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric: [math]g_{\mu \nu} = \eta_{\mu \nu} + h_{\mu \nu}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 1: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R \left(\eta_{\mu \nu} + h_{\mu \nu} \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity weak field limit spacetime metric and Planck quantum gravity identity 2: [math]\boxed{8 \pi T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) - \frac{1}{2} R \left(\eta_{\mu \nu} + h_{\mu \nu} \right)}[/math] [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf

Affirmative, that is correct. [math]\;[/math] Einstein's field equations: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = \frac{8 \pi G}{c^{4}} T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations in natural units: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} = 8 \pi T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations Ricci tensor in natural units: [math]\boxed{ R_{\mu \nu} = 8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}[/math] [math]\;[/math] Lagrangian equation: [math]\mathcal{L} = \underbrace{ \mathbb{R} }_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0[/math] [math]\;[/math] General relativity Lagrangian equation: [math]\boxed{\mathcal{L} = \underbrace{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] A massless gravitational wave is still massless on a Planck scale, and the result is still a tensor field. [math]\;[/math] Tensor field: (ref. 1, pg. 21, eq. 1.68) [math]T^{' \mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] The general relativity Ricci tensor is a tensor field: [math]\boxed{R_{\mu \nu} = T^{' \mu \nu} \left(x' \right)}[/math] [math]\;[/math] Lagrangian equation for a massless Planck graviton: [math]\boxed{\mathcal{L} = \underbrace{ \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right) }_{QG} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] General relativity and Planck quantum gravity identity: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R g_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] General relativity spacetime metric: [math]g_{\mu \nu} = \eta_{\mu \nu} + h_{\mu \nu}[/math] [math]\;[/math] General relativity spacetime metric and Planck quantum gravity identity: [math]\boxed{8 \pi T_{\mu \nu} + \frac{1}{2} R \left(\eta_{\mu \nu} + h_{\mu \nu} \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right)}[/math] [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf

[math]\;[/math] Affirmative, according to Wikipedia, The action S is given by: [math]S = -mc \int ds = \int L dt[/math] [math]\;[/math] Where L is the relativistic Lagrangian for a free particle: [math]L = -mc^{2} \sqrt{1 - \frac {v^{2}}{c^{2}}}[/math] [math]\;[/math] And my solution for the proper time relativistic Lagrangian for a free particle: [math]\boxed{\mathcal{L} = - \frac{m_{0} c^{2}}{\gamma\left(\dot{\mathbf{r}} \right)} = -m_{0} c^2 \sqrt{1 - \frac{\dot{\mathbf{r}}^2 \left(t \right)}{c^2}}}[/math] [math]\;[/math] [math]\;[/math] A free particle that encounters a gravity field potential will always form a closed path in x,y,z, and time dilation t, and invoke Keplers laws: [math]L = - \frac{m_0 c^2}{\gamma\left( \dot{\mathbf{r}} \right)} - V\left(\mathbf{r}, \dot{\mathbf{r}}, t \right)[/math] [math]\;[/math] [math]\mathbf{v} = \dot{\mathbf{r}} = \frac{d\mathbf{r}}{dt} = \left(\frac{dx}{dt} , \frac{dy}{dt} , \frac{dz}{dt} \right)[/math] [math]\;[/math] Except in the case for a hyperbolic trajectory with escape velocity, where the path integral is inflection curved at the point source for the gravitational field potential. [math]\;[/math] Because, It is implied that the Ricci tensor is still the classical theory of general relativity in this form. Affirmative, I think that you have answered your own question. [math]\;[/math] Einstein's field equations: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{R g_{\mu \nu}}{2} = \frac{8 \pi G}{c^{4}} T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations in natural units: [math]G_{\mu \nu} = R_{\mu \nu} - \frac{R g_{\mu \nu}}{2} = 8 \pi T_{\mu \nu}[/math] [math]\;[/math] Einstein's field equations Ricci tensor in natural units: [math]\boxed{ R_{\mu \nu} = 8 \pi T_{\mu \nu} + \frac{R g_{\mu \nu}}{2} }[/math] [math]\;[/math] Lagrangian equation: [math]\mathcal{L} = \underbrace{ \mathbb{R} }_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0[/math] [math]\;[/math] General relativity Lagrangian equation: [math]\boxed{\mathcal{L} = \underbrace{8 \pi T_{\mu \nu} + \frac{R g_{\mu \nu}}{2}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] Conventional gravitational waves that are quantized below the Planck radius with a total Planck energy would be indistinguishable from what scientists refer to as gravitons. Absent a total Planck energy available to generate them, scientists will never observe them to add them to the standard model. [math]\;[/math] A massless gravitational wave is still massless on a Planck scale, and the result is still a tensor field. [math]\;[/math] Tensor field: (ref. 1,pg. 21, eq. 1.68) [math]T^{' \mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] Lagrangian equation for a massless Planck graviton: [math]\boxed{\mathcal{L} = \underbrace{ \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right) }_{QG} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0}[/math] [math]\;[/math] General relativity and Planck quantum gravity identity: [math]\boxed{8 \pi T_{\mu \nu} + \frac{R g_{\mu \nu}}{2} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)}[/math] [math]\;[/math] Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf

Relativistic Lagrangian Lorentz factor: (ref. 1, ref. 2, ref. 6) [math]dt = \gamma\left(\dot{\mathbf{r}} \right) d\tau[/math] [math]\;[/math] [math]\gamma\left(\dot{\mathbf{r}} \right) = \frac{dt}{d\tau} = \frac{1}{\sqrt{1 - \frac{\dot{\mathbf{r}}^2}{c^2}}}[/math] [math]\boxed{\gamma\left(\dot{\mathbf{r}} \right) = \frac{1}{\sqrt{1 - \frac{\dot{\mathbf{r}}^2}{c^2}}}}[/math] [math]\;[/math] [math]\dot{\mathbf{r}} = \frac{d\mathbf{r}}{dt}[/math] [math]\;[/math] Relativistic Lagrangian neutral particle total energy integration via substitution: (ref. 2) [math]E_{t} = m_0 c^2 \frac{dt}{d \tau} = \gamma\left(\dot{\mathbf{r}} \right) m_0 c^2 = \frac{m_0 c^2}{\sqrt {1 - \frac{\dot{\mathbf{r}}^2 \left(t \right)}{c^2}}} = m_0 c^2 + {1 \over 2} m_0 \dot{\mathbf{r}}^2 \left(t \right) + {3 \over 8} m_0 \frac{\dot{\mathbf{r}}^4 \left(t \right)}{c^2} + \cdots[/math] [math]\;[/math] Relativistic Lagrangian neutral particle total energy: (ref. 2) [math]\boxed{E_{t} = \frac{m_{0} c^2}{\sqrt{1 - \frac{\dot{\mathbf{r}}^2 \left(t \right)}{c^2}}}}[/math] [math]\;[/math] Classical neutral particle kinetic energy: [math]E_{k} = \frac{m_{0} v^{2}}{2} = \frac{m_{0}}{2} \frac{ds^{2}}{dt^{2}}[/math] [math]\boxed{E_{k} = \frac{m_{0}}{2} \frac{ds^{2}}{dt^{2}}}[/math] [math]\;[/math] Classical Lagrangian neutral particle kinetic energy: (ref. 4) [math]E_{k} = \frac{m_{0} g_{bc}}{2} \frac{\mathrm{d}\xi^{b}}{\mathrm{d}t} \frac{\mathrm{d}\xi^{c}}{\mathrm{d}t}[/math] [math]\;[/math] Relativistic Lagrangian neutral particle kinetic energy: [math]E_{k} = m_{0} c^{2} \left(\gamma\left(\dot{\mathbf{r}} \right) - 1 \right)[/math] [math]\;[/math] Newtons second law for neutral particle integration via substitution: (ref. 3) [math]\mathbf{F} = \frac{d \mathbf{p}}{dt} = \frac{d(m_{0} \mathbf{v})}{\mathrm{d}t} = m_{0} \frac{d\mathbf{v}}{\mathrm{d}t} = m_{0} \frac{ds}{dt^2}[/math] [math]\;[/math] Newtons second law for neutral particle: [math]\boxed{\mathbf{F} = m_{0} \frac{ds}{dt^2}}[/math] [math]\;[/math] Relativistic Newtons second law for neutral particle: [math]\boxed{\mathbf{F} = \gamma m_{0} \frac{ds}{dt^2}}[/math] [math]\;[/math] General relativity geodesic equation: (ref. 4) [math]\frac{d^{2}x^{\mu}}{dt^{2}} + \Gamma^{\mu}{}_{\alpha \beta} \frac{dx^{\alpha}}{dt} \frac{dx^{\beta}}{dt} = 0[/math] [math]\;[/math] Newtons second law in Lagrangian form for neutral particle: (ref. 5) [math]F^{a} = m_{0} \left(\frac{d^{2} \xi^{a}}{dt^{2}}+ \Gamma^{a}{}_{bc} \frac{d\xi^{b}}{dt} \frac{d\xi^{c}}{dt} \right)[/math] [math]\;[/math] Relativistic Newtons second law in Lagrangian form for neutral particle: [math]\boxed{F^{a} = \gamma\left(\dot{\mathbf{r}} \right) m_{0} \left( \frac{d^{2} \xi^{a}}{dt^{2}} + \Gamma^{a}{}_{bc} \frac{d\xi^{b}}{dt} \frac{d\xi^{c}}{dt} \right)}[/math] [math]\;[/math] Relativistic Lagrangian for a neutral particle: [math]\mathcal{L} = E_{k} - E_{p}[/math] [math]\;[/math] [math]\boxed{\mathcal{L} = m_{0} c^{2} \left(\gamma\left(\dot{\mathbf{r}} \right) - 1 \right) - E_{p}}[/math] [math]\;[/math] Relativistic Lagrangian integration via substitution: [math]\mathcal{L} = \sum_{1}^{n} E_{k}\left(n \right) - \sum_{1}^{n} E_{p}\left(n \right) = \sum_{1}^{n} \mathcal{L}\left(n \right) = 0[/math] [math]\;[/math] Relativistic Lagrangian: [math]\boxed{\mathcal{L} = \sum_{1}^{n} \mathcal{L}\left(n \right) = 0}[/math] [math]\;[/math] The Lagrangian equation integration via substitution: [math]\mathcal{L} = \sum_{1}^{n} \mathcal{L}\left(n \right) = \underbrace{\mathbb{R}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0 \; \; \; \; \; \; n = 5[/math] The Lagrangian equation: [math]\boxed{\mathcal{L} = \underbrace{\mathbb{R}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0} \; \; \; \; \; \; n = 5[/math] [math]\;[/math] [math]\;[/math] I think that this revision has compensated for the 4 momentum and 4 velocity under general relativity with respect to proper time [math]\tau[/math], through the Lorentz factor. The 4 momentum and 4 velocity is intrinsic to general relativity as required by four-dimensional space-time. [math]\;[/math] I note two general relativity geodesic equation forms, a spacial and a temporal form. [math]\;[/math] General relativity spacial geodesic equation: (ref. 4) [math]\frac{d^{2}x^{\mu}}{ds^{2}} + \Gamma^{\mu}{}_{\alpha \beta} \frac{dx^{\alpha}}{ds} \frac{dx^{\beta}}{ds} = 0[/math] [math]\;[/math] General relativity temporal geodesic equation: (ref. 4) [math]\frac{d^{2}x^{\mu}}{dt^{2}} + \Gamma^{\mu}{}_{\alpha \beta} \frac{dx^{\alpha}}{dt} \frac{dx^{\beta}}{dt} = 0[/math] [math]\;[/math] Do you agree with this mathematical symbolic formalism derivation revision for the formal Lagrangian equation? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - The Lorentz factor: (ref. 1) https://en.wikipedia.org/wiki/Lorentz_factor Wikipedia - Relativistic Lagrangian mechanics: (ref. 2) https://en.wikipedia.org/wiki/Relativistic_Lagrangian_mechanics#Coordinate_formulation Wikipedia - Newtons second law: (ref. 3) https://en.wikipedia.org/wiki/Newton's_laws_of_motion#Newton's_second_law Wikipedia - Geodesics in general relativity: (ref. 4) https://en.wikipedia.org/wiki/Geodesics_in_general_relativity Wikipedia - Newtons second law Lagrangian form: (ref. 5) https://en.wikipedia.org/wiki/Lagrangian_mechanics#From_Newtonian_to_Lagrangian_mechanics Wikipedia - Four-velocity: (ref. 6) https://en.wikipedia.org/wiki/Four-velocity

[math]\;[/math] Please consider Newtons second law and the relativistic Newtons second law for a moment. [math]\;[/math] [math]\gamma[/math] - Lorentz factor [math]\;[/math] Newtons second law: (ref. 1) [math]\mathbf{F} = \frac{d \mathbf{p}}{dt} = \frac{d\left(m \mathbf{v} \right)}{\mathrm{d}t} = m {\frac{d\mathbf{v}}{\mathrm{d}t}} = m \frac{ds}{dt^2}[/math] [math]\boxed{\mathbf{F} = m \frac{ds}{dt^2}}[/math] [math]\;[/math] Relativistic Newtons second law: [math]\boxed{\mathbf{F} = \gamma m \frac{ds}{dt^2}}[/math] [math]\;[/math] Newtons second law in Lagrangian form: (ref. 2) [math]F^{a} = m \left( \frac{d^{2} \xi^{a}}{dt^{2}}+ \Gamma^{a}{}_{bc} \frac{d\xi^{b}}{dt} \frac{d\xi^{c}}{dt} \right)[/math] [math]\;[/math] Relativistic Newtons second law in Lagrangian form: [math]\boxed{F^{a} = \gamma m \left( \frac{d^{2} \xi^{a}}{dt^{2}}+ \Gamma^{a}{}_{bc} \frac{d\xi^{b}}{dt} \frac{d\xi^{c}}{dt} \right)}[/math] [math]\;[/math] Thus including all classical nonrelativistic Lagrangian mechanics into relativistic Lagrangian mechanics? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Newtons second law: (ref. 1) https://en.wikipedia.org/wiki/Newton's_laws_of_motion#Newton's_second_law Wikipedia - Newtons second law in Lagrangian form: (ref. 2) https://en.wikipedia.org/wiki/Lagrangian_mechanics#From_Newtonian_to_Lagrangian_mechanics

I request to initiate a thread on what I only know as the Lagrangian equation. The original published scientific paper derivation proof is unknown to me. [math]\;[/math] Lagrangian equation: [math]\mathcal{L} = \underbrace{\mathbb{R}}_{GR} - \overbrace{\underbrace{\frac{1}{4} F_{\mu \nu} F^{\mu \nu}}_{Yang-Mills}}^{Maxwell} + \underbrace{i \overline{\psi} \gamma^\mu D_\mu \psi}_{Dirac} + \underbrace{|D_\mu h|^2-V\left(|h| \right)}_{Higgs} + \underbrace{h \overline{\psi} \psi}_{Yukawa} = 0[/math] [math]\;[/math] This Lagrangian equation appears to represent a massless field tensor fundamental field interaction Lagrangian combination zero summation action in natural units. [math]\;[/math] The classical General Relativity Lagrangian tensor appears to describe a Ricci tensor on a smooth spacially flat Ricci maniold [math]\mathbb{R}[/math]. (ref. 1, ref. 2) [math]\;[/math] The massless field tensor Yang-Mills Maxwell Lagrangian term represents at the core of the unification of the electromagnetic force and weak forces [math](U(1) \times SU(2))[/math] and quantum chromodynamics, the theory of the strong force [math](SU(3))[/math] and predicts all the massless spin one Maxwells equations. (ref. 3, ref. 4) [math]\;[/math] The massless field tensor Dirac Lagrangian term is a relativistic wave equation that describes all spin one-half particle interactions. (ref. 5) [math]\;[/math] The massless field tensor Higgs Lagrangian term describes all spin zero Higgs field interactions. (ref. 6) [math]\;[/math] The massless field tensor Yukawa coupling interaction term describes the interaction between a massless spin zero scalar field [math]\phi[/math] and a massless spin one-half Dirac field [math]\psi[/math] (ref. 7) [math]\;[/math] Do you know where the original published scientific paper derivation proof is located? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Ricci curvature: (ref. 1) https://en.wikipedia.org/wiki/Ricci_curvature Wikipedia - Riemannian manifold: (ref. 2) https://en.wikipedia.org/wiki/Riemannian_manifold Wikipedia - Maxwells equations: (ref. 3) https://en.wikipedia.org/wiki/Maxwell's_equations#Formulation_in_SI_units_convention Stackexchange - derivation of maxwells equations from field tensor lagrangian: (ref. 4) https://physics.stackexchange.com/questions/3005/derivation-of-maxwells-equations-from-field-tensor-lagrangian Wikipedia - Dirac Lagrangian: (ref. 5) https://en.wikipedia.org/wiki/Dirac_equation#Dirac_Lagrangian Wikipedia - Higgs field: (ref. 6) https://simple.wikipedia.org/wiki/Higgs_field Wikipedia - Yukawa Lagrangian: (ref. 7) https://en.wikipedia.org/wiki/Yukawa_interaction#The_action

This is true for the Compton equation, where a mass-less particle is scattering from a mass particle. However, in equation [math](6)[/math], the energy terms for [math]E[/math] represent the total energy of a mass particle, which includes its rest mass plus kinetic energy. I should have been more clear about that equation description and will include the total energy description in the next revision, hence peer review. If I understand this inelastic scattering correctly, when a lighter particle scatters from a heavier particle, as total kinetic energy is increased, then more kinetic energy is absorbed by the recoiling heavier particle and less kinetic energy is carried away by the lighter particle. So, the limit of equations [math](12)[/math] and [math](13)[/math] as kinetic energy approaches infinity, should be the rest mass of the neutrino. [math]\lim_{E_k \to \infty} m_{\nu} = m_{\nu,0}[/math]

Derivation of neutrino mass from neutrino scattering: [math]\theta[/math] - scattered neutrino angle [math]\phi[/math] - electron recoil angle [math]p_{i}[/math] - initial neutrino momentum [math]p_{f}[/math] - final neutrino momentum [math]p_{e}[/math] - electron momentum [math]p_{e} \sin \phi = p_{f} \sin \theta \tag{1}[/math] [math]p_{e} \cos \phi + p_{f} \cos \theta = p_{i} \tag{2}[/math] Isolate [math]p_{e} \cos \phi[/math] from equation [math](2)[/math]: [math]p_{e} \cos \phi = p_{i} - p_{f} \cos \theta \tag{3}[/math] Divide equation [math](1)[/math] by equation [math](3)[/math] for an expression for [math]\tan \phi[/math]: [math]\tan \phi = \frac{p_{f} \sin \theta}{p_{i} - p_{f} \cos \theta} = \frac{\sin \theta}{\frac{p_{i}}{p_{f}} - \cos \theta} \tag{4}[/math] Acquire a substitution for [math]\frac{p_{i}}{p_{f}}[/math] to eliminate [math]p_{f}[/math]. Use the Compton equation, which can be rearranged to yield [math]\frac{\lambda_{f}}{\lambda_{i}} = \frac{p_{i}}{p_{f}}[/math] in terms of [math]\lambda_{i}[/math] alone, noting that [math]p = \frac{E}{c}[/math]. [math]\lambda_{f} - \lambda_{i} = \frac{h}{m_{e} c} (1 - \cos \theta) \tag{5}[/math] [math]\frac{\lambda_{f}}{\lambda_{i}} = \frac{p_{i}}{p_{f}} = 1 + \frac{E_{\nu}}{E_{e}} (1 - \cos \theta) = 1 + \frac{m_{\nu} c^2}{m_{e} c^2} (1 - \cos \theta) = 1 + \frac{m_{\nu}}{m_{e}} (1 - \cos \theta) \tag{6}[/math] Substituting equation [math](6)[/math] into equation [math](4)[/math], and eliminate [math]p_{i}[/math] and [math]p_{f}[/math] in favor of [math]m_{\nu}[/math] alone. [math]\tan \phi = \frac{\sin \theta}{\frac{p_{i}}{p_{f}} - \cos \theta} = \frac{\sin \theta}{1 + \frac{m_{\nu}}{m_{e}} (1 - \cos \theta) - \cos \theta} = \frac{\sin \theta}{\left(1 + \frac{m_{\nu}}{m_{e}} \right)(1 - \cos \theta)} \tag{7}[/math] Utilizing a trigonometric identity produces the desired result, specifically: [math]\frac{1 - \cos \theta}{\sin \theta} = \tan \left(\frac{\theta}{2} \right) \tag{8}[/math] Substituting this trigonometric identity into equation [math](7)[/math] results in: [math]\left(1 + \frac{m_{\nu}}{m_{e}} \right) \tan \phi = \cot \frac{\theta}{2} \tag{9}[/math] Solve for neutrino mass [math]m_{\nu}[/math]: [math]\tan \phi + \frac{m_{\nu}}{m_{e}} \tan \phi = \cot \frac{\theta}{2} \tag{10}[/math] [math]\frac{m_{\nu}}{m_{e}} \tan \phi = \left(\cot \frac{\theta}{2} - \tan \phi \right) \tag{11}[/math] Electron-neutrino scattering neutrino mass: [math]\boxed{m_{\nu} = m_{e} \cot \phi \left(\cot \frac{\theta}{2} - \tan \phi \right)} \tag{12}[/math] Nuclear-neutrino scattering neutrino mass: [math]\boxed{m_{\nu} = m_{n} \cot \phi \left(\cot \frac{\theta}{2} - \tan \phi \right)} \tag{13}[/math] [math]m_{n}[/math] - nuclear mass Electron interaction neutrino scattering angle [math]\theta[/math]: [math]\boxed{\theta = 2 \operatorname{arccot} \left(\frac{(m_{e} + m_{\nu}) \tan \phi}{m_{e}} \right)} \tag{14}[/math] Neutrino interaction electron recoil angle [math]\phi[/math]: [math]\boxed{\phi = \arctan \left(\frac{m_{e} \cot \frac{\theta}{2}}{m_{e} + m_{\nu}} \right)} \tag{15}[/math] Nuclear interaction neutrino scattering angle [math]\theta[/math]: [math]\boxed{\theta = 2 \operatorname{arccot} \left(\frac{(m_{n} + m_{\nu}) \tan \phi}{m_{n}} \right)} \tag{16}[/math] Neutrino interaction nuclear recoil angle [math]\phi[/math]: [math]\boxed{\phi = \arctan \left(\frac{m_{n} \cot \frac{\theta}{2}}{m_{n} + m_{\nu}} \right)} \tag{17}[/math] Any discussions and/or peer reviews about this specific topic thread? Reference: Wikipedia - Compton scattering - Derivation of the scattering formula: https://en.wikipedia.org/wiki/Compton_scattering#Derivation_of_the_scattering_formula Physics 253 - Compton Scattering - Patrick LeClair: http://pleclair.ua.edu//PH253/Notes/compton.pdf Orion1 - Neutrino mass from Fermi-Dirac statistics...: https://www.scienceforums.net/topic/90189-neutrino-mass-from-fermi-dirac-statistics/ Science News - Neutrinos seen scattering off an atom’s nucleus for the first time: https://www.sciencenews.org/article/neutrinos-seen-scattering-atoms-nucleus-first-time