studiot

Well, I did wonder. But Google has plenty on 'politis' a Greek concept of a citizen and his rights and duties. So my question stands. As regards lobsters, I remember some years back visiting the Aquarium and Marine Biology labs whilst on holiday in Pembrokeshire. I was impressed with the work and projects they had going on with local schools. One project was a huge tank for the study of the marine environment. Listening to the guide I learend that the marine invornment was far closer to the 'law of the jungle' than ouit own. Everything was easy prey to something and even fierce looking creatures like lobsters would be quicly gobbled up if they strayed too far from their shelter. Definitely a constantly dangerous and aggressive environment.

Can anyone tell me what is meant by Politis in thread title ? It's all Greek to me. I also wonder if, having been mentioned in the current BBC drama, JP will become a latter day Harvey Smith ?

The response from the art world. https://www.bbc.co.uk/news/uk-england-derbyshire-59318780

Hi Chris, the two most important Laws in Science are called the first and seconf Law of Thermodynaics. They are the most important in my opinion, because they enabled the industrial revolution. The first law states "You can't get something for nothing" or "There is no such thing as a free lunch" or "You can't win, you can only break even". The second law states "You can't even break even you can only loose" So think of an ordinary coal or log fire. In theory you could collect all the heat from the combustion and use that as well as the portion you actually use. But the first law tells you that you can only get out what you put in. That is for a specific amount of fuel you get a specific amount of heat and no more. However the second law bites you in the ass because some of the products of combustion appear as a gas and go up the chimney. But to make a gas from a solid or liquid (fuel) requires an input of heat energy. This heat can only come from the heat of combustion as ther is nowhere else for it to come from. If the combustion products did not go up the chimney they would collect in the fireplace. Similarly if you took all the energy out of the water passing through a turbine at the bottom of a dam, the water would unot have enough energy left to flow away and you would be faced with a flood. At each stage of any process there Mr 10% (or worse) always takes his cut. So every time you recycle your hydrogen you would loose 10% (it would actually be more). Does this help ?

You mean Vance Packard ?

That is not, and never has been, the situation I described. As it is clear you are not going to even attempt to follow my question, let alone begin to answer it, we are done here with your fairy tales.

An excellent. and satisfying short, summary of what everyone has been saying to you. +1

The question you asked me on Nov 9 was, “Re phrasing for absorbtion, Are you telling me you that the electron can 'jump' before absorbtion takes place ? Surely the fundamental question is Which must happen first, absorption, or the electron transition ? “ The question strikes me as asking, Which came first, the shell or the nut? For one thing, you can’t tell precisely when the transition took place because of the impossibility of observing the event and the terms absorption and transition are essentially synonymous. My answer was that I can’t possibly see how anyone can time the events. I could have guessed and said absorption comes first. I suspect that is the answer you were looking for but that is not an answer I can support since I see the timing as unknowable. I have no idea where you are going with your “spectral lines” example so I expect you to explain whatever you are trying to explain. The problem can be viewed theoretically as a problem of math and this has been done by Carver Mead. Carver Mead is a former colleague of Richard Feynman and well known for his innovative work with transistors and IC’s so I suspect he knows what he is talking about. Mead's calculations are time-symmetric with waves going simultaneously forward and backward in time so the concepts of first and last are meaningless. The calculations can be found in the book “Collective Electrodynamics” by Carver Mead in Part 5 “Electromagnetic Interaction of Atoms.” The time of duration in his equations is represented by the letter alpha. I don’t understand Mead’s calculations well enough to give a reliable explanation but it is obvious from his descriptions that he has moved on from photon theory. This is not quite what I am saying. I am saying that two separate particles with different quantum states can share a common existence as if they were side-by-side even though they may be light centuries apart. More specifically, an electron in one part of the universe can share energy with an electron in a another part of the universe by means of entanglement so long as they reside on the same light cone. But, with all that waffle, you still have not addressed my question. You have just tried to sweep it under the carpet. I would hazard a guess that everyone else reading this thread can see that I have tried to ask the same question in different ways in order to try to make it as clear as I possibly can. Rephrasing sometimes helps. However you persistently address different questions, from the one I asked you. Of course not, you are answering a differnt question that you posed to yourself. Easy sidestep. Whether we are able to measure something or not has no bearing on that something itself. It would still be the same, even if we did not exist at all to attempt a measurement. So as not to appear grumpy and churlish I will offer a line of analytical thinking in more detail. A great many of our achievements in Science and Engineering are founded on the technique considering a very small piece of something and then considering what happens to our theory when we shrink that piece to zero. So consider an electron gaining energy by absorbtion, with a start time and a finish time separated by a very small time interval. (Note I have not specified absorbtion of any type of EM radiation, just energy from whatever source. Such non EM sources undoubtedly exist and are studied in basic physics.) Now QM tells us that the electron cannot make the transition to the higher state until the entire quantity of energy is available, whenever that occurs. Perhaps it cannot even start that transition until that point in time is reached. So we now consider a transition of the electron with its own, yet to be defined, start and end points, which correspond to different states of the electron (by definition) Put these together in a critical path analysis and then see what happens as you shrink either or both to zero. 'Instantaneous' would require both these very short time intervals to be exactly zero. Which would imply that the electron is in two different states at once. Still the same question, just with more detail. Schrodinger asked it way back about his cat.

+1 for another well thought out and balanced assessment. (Background sounding of Copland's "fanfare for the common man") You have advanced the cause of rational thinking by "non experts" substantially. More so in my opinion that the subject of this thread, even though I have little symapthy for him. Hi MigL, I am going to both agree with you and disagree with you. Yes I agree that I find current Psychology , as a Science, at about the level of Physics in the time of Francis Bacon. They are just beginning to find their way by feeling for the variables/parameters to observe and consider. As such they have yet to develop any really effective tools, just as mechanics was before Gallileo and Newton. Today we know a lot more about mechanics (who would be brave/foolish enough to say we know everything ?). In particular I am suprised at your declaration of repeatabilty. Yes it is a desirable outcome, but not always attainable, even in mechanics. We know of at least three factors that mitigate against the possibility of repeatabilty. 1) Statistical variation, leading to the development of limit state theory amongst other techniques. 2) Chaos theory leading to multiple (unrepeatable) outcomes. 3) Catastrophe theory, leading to uncertainty of timing of a mechanical outcome.

I tied mine once nearly 2 years ago, to the correct tension and have not needed to tie them again. The masks have now been through the wash at least once a week since then.

My wife did a similar thing, except she cut up some old tights for the material to make the stretchy ties at the back. She has also been experimenting with the metal strips recovered from the hospital blue masks which are re-deformable. As a matter of interest the blue masks survive trips thropugh the wahing machine.

I agree but this is a duplicate thread of this one

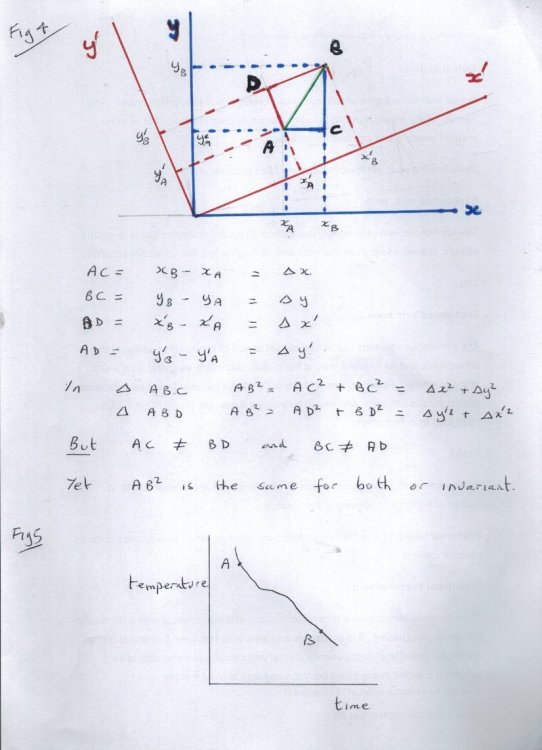
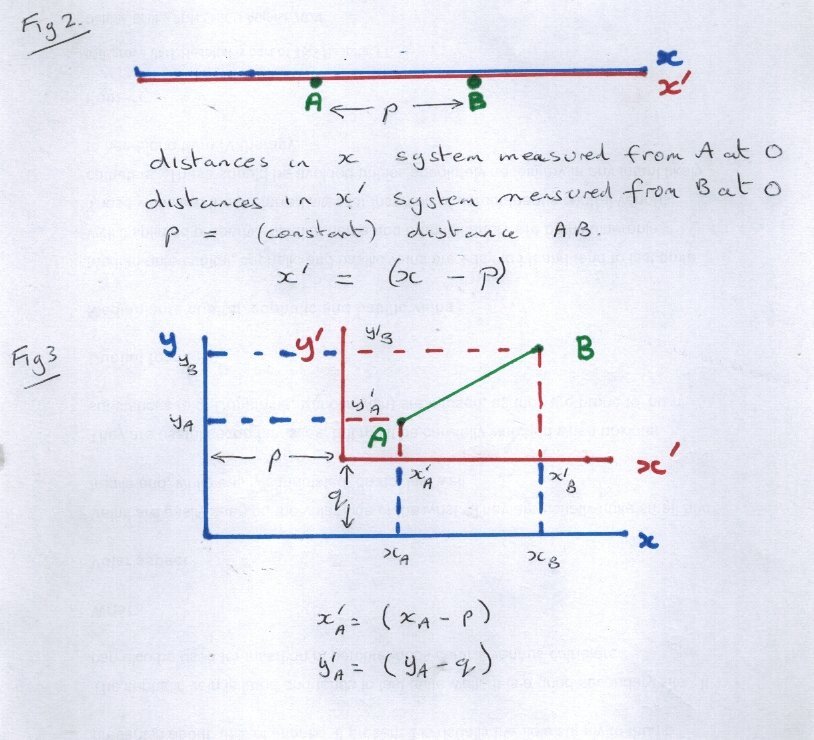
Ok so I have been doodling over the weekend, but sadly did not get as far as I had hoped. So here is the next part. Fig 2 is a repeat of Fig 1 but introducing two coordinate systems. In the red corner we have the red system. x', and in the blue corner we have the blue system x. Note the constant p yields a 'transfomation' equation between the two systems. We can also show that the the distance between A and B have the same value in both systems, following the equations in Fig1. That is it is invariant. I will return to the x' = (x - p) equation in more detail, when we get on to motion. In Fig 3 we strike out in 2 dimensions, with two displacement constants, p and q. Now that we are using the full extent of our graph paper, I have tilred the line AB, shown in green. Hopefully it is easy to see that the length of this line is [math]\sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} = \sqrt {{{\left( {x{'_B} - x{'_A}} \right)}^2} + {{\left( {y{'_B} - y{'_A}} \right)}^2}} [/math] although the coordiante differences are different for the red and blue systems. Displacement of a coordinate system is a 'permitted transformation' that simply move the origin about on the graph paper. The other permitted transformation is a rotation of the soordinate system, as in Fig 4 I have gone explicitly through the geometry to show how once again the length AB or its square AB2 is invariant, regardless of the angle of rotation. The key to this is to note that the length AB is the common hypotenuse to two triangles, ABC in the blue system and ABD in the red system. So for rotation also the length is measured the same in both systems That wraps up the static situation, but what ae we actually doing ? We are drawing lines on a piece of graph paper. All lines on that graph paper have a length measured in, say, cm. That is both axis lines, gridlines and plotted lines. To attach meaning to this look at Fig 5, which is a cooling curve for some substance, and a 'plot' of temperature against time. What units is the distance along the curve between points A and B measured in ? Well like all lines on the graph paper, it is measured in cm But, you say, the axes are in seconds and degrees C. No they are also measured, on the graph, in cm. Bot axes are subject to a scale factor (constant in this case) that introduces the necessary conversion of units. Cm to seconds and cm to degrees, remembering that we can only plot cm on the graph paper. This is where you question about c comes in. c is a velocity and velocity is a (variable or constant) scale factor converting time to length. The next installment will introduce moving coordinate systems, which are the basis of relativity. There are three things we must take forward from this. Firstly that there are invariants that are measured the same in all coordinate systems. Secondly The most important one is a function of coordinate difference, not the coordinates themselves. Thirdly that all we have been considering is Geometry, as in the shape and size of things.

And yet they are popular in Scandinavia. I have no idea what you mean by this ?

Some explanation of your diagrams would help and perhaps draw more discussion. I, for one, have no idea what you are showing in your diagrams. Perhaps also you could fill in the blank space following your here is some more comment ?

I suggest another way of looking at it is to say that classical mechanics (of the sort we have been talking about) is about localisation, quantum mechanics is about delocalisation. I was at Loughborough in 1968, 69 and 70. The Chemistry department was dwarfed by the Chemical Engineering department. The Physics department was even smaller than the Chemistry. But that is all a long story.

Seems to me that the 'environment' is shown at the sides (ends) of the waveforms using the standard ground symbols. The particle in a box is certainly not isolated since it is in a box. QM does offer an analysis of a body under no constraints ie a freely moving particle. But then a free body diagram with no replacement forces is a bit trivial.

I can't resist this, although google fought man and boy to resist offering anything for hat pump. As to your legitimate question. Yes some extra loft insulation was done but things like cavity wall, high grade double glazing, swapping old metal frames for solid mahogany, underfloor insulation were all done years before the heat pump. No costs of the extra loft insulation were included in the opening post.

I have a great deal of respect for Proff Atkins and several of his books. Funny, when I was first at university most of the important names of british chemistry books were light blue, eg Moelwyn-Hughes. One thing that I recall is the difference between classical and quantum systems. You cannot divorce a quantum system from its environment, there are no 'free body diagrams' in QM.

To answer in your own words and stop hijacking mine with off topic material ?

Thanks for pointing out my spelling error.

I suppose it depends how you weigh out your crimes. The theft of a loaf of bread or a clean new pair of trousers, when you don't have enough money for food, shelter etc, = 2 crimes or 2 criminals. Whereas mass murder by the million, when you have more than enough of everything, counts as only one ?

What experience and figures do you present to back up this claim ?

I get the impression from the News that the biggest crimes are committed by some of the most influential/richest/important people. So it is neither true nor fair to conflate being poor and being a criminal.

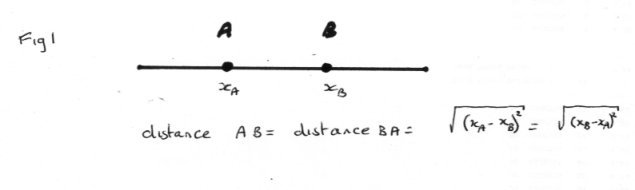
Ok to continue where I left off. Just to point out that I am offering backgound explanations and insights that you won't find in any one textbook. If you just want a formal development, there are many good presentations on offer. The official title is not 'spacetime' but 'the spacetime continuum'. A continuum is a grid or framework of points where at every point the properties of interest are the same. This expresses the idea of homogeneity, which is also inherent in the Principle of Relativity. For instance take a piece of squared graph paper. It is a continuum. A geometric continuum. A finite continuum, since the paper has edges, but a continuum nonetheless. The graph paper has no 'origin'. We can impose an origin at any point by imposing a pair of axes. And impose scales marked on the paper. This then gives a particular coordinate system to the grid. It also gives us a large number of possible different coordinate systems. I will start with static coordinate systems (which do not need time) before proceeding to moving coordinate systems (which do need time). For completeness I will start with one dimensional (ie one axis only, the x axis) coordinate systems. Coordinate systems are also called 'frames' , and will introduce the motivation for this name. The importance of one dimension is that it gives us a definition of length or distance between any two points A , B in the continuum as in fig (1). We use the rather awkward looking square root of the square of the difference in coordinates, xA and xB because this makes the distance from A to B the same as the distance from B to A and also makes this a positive or zero (ie nonnegative) quantity, which is only zero if A and B are the same point. [math]\sqrt {{{\left( {{x_A} - {x_B}} \right)}^2}} = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2}} [/math] Note. This conforms to the mathematics definition of a metric or distance function. Metrics in Physics can also be negative and Relativity explores what happens when the metric in Physics is negative. Another mathematical nicety is that the modulus or absolute value |xA-xB| can also be used as a metric, but has the disadvantage that it is not differentiable at zero. Work in progress to be continued.