-
Posts
7713 -
Joined
-
Last visited
-
Days Won
26
Sensei last won the day on October 27 2023
Sensei had the most liked content!
Profile Information
-
Interests
Quantum Physics, C/C++/.NET Framework/Java programming.
-
Favorite Area of Science
Quantum Physics
Recent Profile Visitors
61889 profile views
Sensei's Achievements

Genius (11/13)
1.3k
Reputation
-

Given the reactions, how many Volts is the yield ?
Sensei replied to Externet's topic in Applied Chemistry
Experimentally. -
The most basic electrical devices consist of the following elements: a resistor, a capacitor and an coil. https://en.wikipedia.org/wiki/Resistor https://en.wikipedia.org/wiki/Capacitor https://en.wikipedia.org/wiki/Inductor The most basic electronic devices have the above elements plus a diode (or equivalent vacuum tube), a transistor (or equivalent vacuum tube), integrated circuits, microcontrollers, and processors. https://en.wikipedia.org/wiki/Diode https://en.wikipedia.org/wiki/Transistor https://en.wikipedia.org/wiki/Vacuum_tube https://en.wikipedia.org/wiki/Integrated_circuit Integrated circuits, microcontrollers and processors are programmable, that is, they execute a program that someone wrote and upload to them or to RAM and/or ROM. Where stands your "steel wool" with the above?
-
No. Human is not a true hermaphrodite for the same reason that man does not have six fingers or six legs, i.e. inheritance of genes from an older generation to a newer one. Errors in DNA reproduction result in the deactivation or even complete loss of part of the genetic code. Once the tetrapodomorphs developed four (premature) legs, and passed them on to the tetrapod, it was very difficult to regain the legs lost in evolution. The same applies to hermaphroditism.
-
..extremely capacious range of knowledge probed to be reduced to a few sentences that will be a farce of an answer.. some people spend live on it.. 7zip is known for using AES-256. https://en.wikipedia.org/wiki/Advanced_Encryption_Standard But what really matters is what block mode.. https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation See the image encoded with ECB block mode: https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#Electronic_codebook_(ECB) The lack of an initialization vector can have bad consequences..
-
Obviously. But the question is whether you or anyone should trust them. ..how will you do that? Obviously not by e-mail, FB, social medias, not by voice by phone.. Which anyone can decrypt with the ZIP password cracking tool for Linux: https://www.kali.org/tools/fcrackzip/ it is the silliest idea to do.. and has nothing to do with "convenience".. unless "convenient" means "total insecurity".. Then what for to password protect it in the first place? in some/typical cases, an image is harder to decipher than plain text.. Protecting against interception of information is one side of the coin. The second side is whether the data that was sent came from a legitimate source.. https://en.wikipedia.org/wiki/Digital_signature https://en.wikipedia.org/wiki/Pretty_Good_Privacy
-
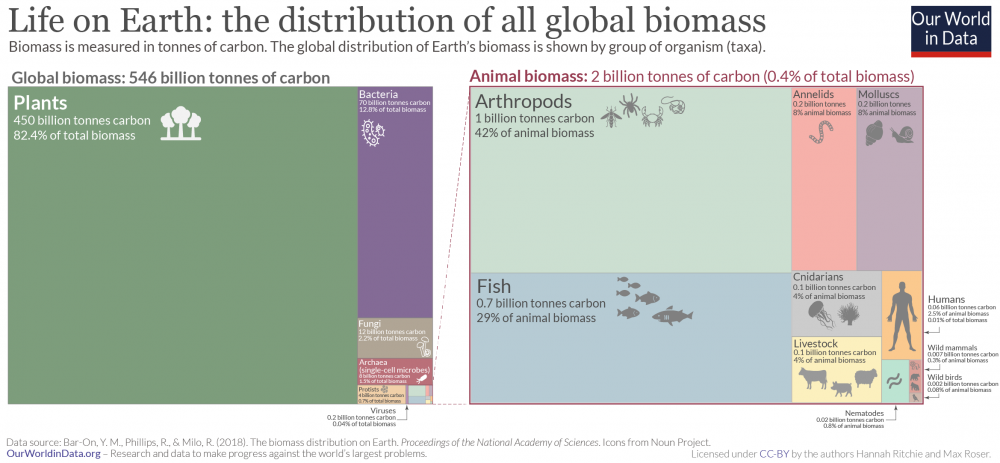
If you look at the biomass of organisms on Earth, you will see that most living organisms do not have sex at all or are hermaphrodites. https://ourworldindata.org/life-on-earth Mammals evolved from reptiles, and these evolved from amphibians, and these evolved from fish. Something that works will not suddenly change into something else because it would disrupt the whole process of fetal development. Changes happen very slowly over millions of years.
-
A regular user does not have access to YouTube cookies.. There are three types of cookies. HTTP cookies, JavaScript local supercookies and JavaScript session supercookies. JS cookies are set and retrieved from JavaScript. HTTP cookies are sent from your browser when you visit the site. They are all stored on the user's computer. Optionally, they may also be stored on the server. It depends on the webmaster/administrators of the visited site. Clearing the cache and cookies does not guarantee no recognition if you visit the same site again. People use Google accounts, Apple IDs, etc. Without a Google account on your smartphone, you can't use the Google Play Store, for example. And every time you visit YouTube, you are asked to sign in, etc. Google stores the IMEI of your smartphones when you create an account, or sign in to the existing account from the next model, i.e. they know that someone sold you a smartphone, gave it to you, that you stole it from someone, that you found someone else's smartphone, etc. etc. You would have to click on his personal website to use any of these cookies. Or he would have to use web beacon on his website. https://en.wikipedia.org/wiki/Web_beacon The amount of knowledge is quite large. He would have to have his own server, know HTML, CSS, JS, PHP, etc. etc. to be able to create such ID theft functionality. And it would work regardless of whether he wrote a YouTube video post or anything else. You wouldn't know that his post was using this technology..
-

Why is the sun moving so fast in this solar eclipse video?
Sensei replied to myname's topic in Other Sciences
Clouds are moving in the foreground, which gives the impression that the sun is moving.. -
Scientists have spent decades on this, a lifetime, and you want us to explain everything to you from scratch. Start from learning how to measure distance to distant stars.. https://en.wikipedia.org/wiki/Stellar_parallax Once you know how to measure distances to near stars, move on to farther stars, then to galaxies, and then to distant galaxies.. If a galaxy is farther away tomorrow than it is today, the obvious conclusion will be that we are receding away.. All this is based on the finite and constant speed of light.
-
I stick to original definition of a lie as something false. The delay in delivering the message is irrelevant here. Otherwise, you can call the Sun a lie, because it is 8 minutes late on the Earth. Which will be ridiculous.
-
Calling it a "lie" to receive correct information with some delay is a serious misuse. The same is true of e-mails, text messages or social networks, where time is counted in milliseconds or even seconds. Lying, as far as I remember, is receiving incorrect information. delay in receiving a message does not make the message false.
-
Not exactly a hydrogen-powered vehicle accident, but a CNG-powered bus. It starts at the 47-second mark if you don't want to listen to the short introduction:
-
C'mon. They want to use liquid Hydrogen inside of regular cars. I have here buses which run on liquid Hydrogen ATM... There are smarter ways to use this precious helium than balloons and airships.