studiot

Sounds like someone is trying to pull the metaphorical atoms of my metaphorical leg to me. Both your statements 1 and 2 are false so I suggest you start again with a proper explanation of what you are trying to say.

If you want to discuss numbers (or anything else) mathematically you need to only use properties that numbers have, not introduce new properties they do not have more especially not when you name those properties something whuch already has a specific mathematical definition as something other than your new properties. I won't both again to say that numbers are not lines and lines are not numbers. You will not find a single number as an element of a set of lines or even the set of all lines. Similarly you will not find a single line as an element of a set of numbers or even the set of all numbers. You keep mentioning a well define property of lines notably distance. How do you define distance ? Numbers do not have this property , they have the property of > < or =, and you must use these to couch you arguments in. Equally, lines do not have the property of + - x or / as well defined operations nor do they follow the normal rules of arithmetic. The conventional way of presenting the notion of a limit as getting closer and closer to something is called the epsilon-delta argument, which involves the normal arithmetic operations along with the less than, greater than or equals notation. Have you heard of this ? I can show you this if you are prepared to listen Are you prepared to listen becasue at the moment you do not seem to be. @Genady has offered you an alternative method via sequences, you don't seem interested in these either. I should warn you that this only works with certain types of sequence called null or Cauchy sequences. They don't. But there is nothing wrong with your comments. A finite range is just the difference between two selected numbers.

The difficulty with answering your queries is how much you do or do not remember from the past. What you need to know here is this minor theorem. Every real number has a decimal representation ( note it is not necessarily unique) So any decimal you can write will be some real number. So is 0.0 repeating a real number. Yes But is 0.0 repeating the smallest real number ? No -1 < 0 So to your worry over an infinite count of zeros after the decimal point, so what ? Pi is well known as and infinite string of digits, as is 0.3 recurring. The process never ends that is what infinity means! Since it never ends, there is no last digit in an infinite string. So the situation you envisage cannot arise. No matter how many noughts you have after the decimal point you can always add another one. This is a fine example of using the wrong words, resulting in nonsense. As is this leading to a statement that is just plain wrong Only some aspects can be thought of geometrically, and only in some circumstances. And distance is not really one of them. Consider this Every number has a square. (theorem) So let us lay out a line of numbers against a line of squares 1,2,3,4,5,6,7,8,9 1,4,,9,16,25,36,49,64,81 Every number on the first line is in one-to-one correspondence with a number on the second line. but the 'lines' have quite a different character.

Well I have yet to see anyone in England that can make a half ways decent paprikash or goulash - or even know the difference - except my late mother. I only wish I could do better than come near her standard. And then her bannocks. I have never been able to replicate those.

Sometimes it is just a question of getting the right words as using popular general ones in their non scientific sense can lead to misunderstandings. 🙂

I only wish that were so. Because I find it really galling to be served something at 5 to 10 times the price of my home cooked and think "I could do much better".. Most folks who sit at my table agree. And I have never poisoned anyone, unlike some self styled high class establishments. When I was first at uni, one of my flatmates came from South Shields. He had a copy of the local rag sporting the headline "Chinese Restaurant Steeps Peas in Toilet." Go figure

Exactly. +1

This simple scheme might help. Which way do you want the maths to go more or less complicated? Which of these real numbers is the next number after 1 ? 1.1 1.01 1.001 1.0001 1.0001 1.00001 1.000001 etc

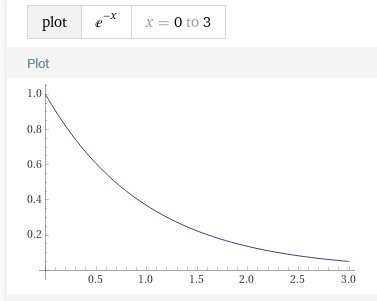
The word point is much overused. I debated with myself how to avoid it as far a possible to avoid confusion. Totally agreed. But I do not like the use of the word end in relation to lines as it can be imprecise. An open interval has no end. I am sorry you missed my main point (there is that word again, but with a different meaning this time) So it means that my explanation was not good enough so I will try to do better. But it is difficult to know what you know as you obviously have met the idea of open and closed intervals before since you used an alternative notation in your responses. I carefully avoided [0,2) etc because it is easy to overlook which bracket is which and you can never be sure whether the writer meant it or not. The reversed square bracket stand out, don't you think ? Also curved brackets are used to denote sets. Anyway you clearly understand that part. My main point was that lines and numbers are not the same, although they have some properties in common, which allows one to exemplify the other when only the common properties are of concern. But sets of numbers have lots of other properties where they cannot be represented as lines. So mathematicians seek more general approaches. If there is a number that is greater than any other number is the set then the set is bounded. In fact we say it is bounded above and can say (similarly it is bounded below if there is a number less than any other number in the set.) So the set (1, 2, 3, 4, 5, 6) is bounded above by the numbers 6, 7, 8, 9, 10... We call any of these an upper bound. Also the upper bound may be an element of the set or it may not. When the upper bound is an element we call it the maximum of the set. Now there is a theorem, which I will not prove, called the least upper bound theorem. "If any set of numbers is bounded above it has a least upper bound" In our example 6 is the least upper bound of our set and is also the maximum. But our set is also finite so it is easy to see this. Finite sets means that the count of elements is finite: Infinite sets have an infinite count of elements. The boundedness theorems apply to finite and to infinite sets, (But not the max and min) Infinite sets can also be bounded. The set of all the elements of the negative exponential e-x, from x=0 to x = ∞ is bounded above by 1 and bounded below by 0, although the set is infinite becasue the count of x values is infinite. Note the x = ∞ 'end' is never reached or as I prefer there is no right hand end to this line. So this line has no minimum. The left hand end depends whether we include or exclude x = 0 in the set (closed or open ) If we include x = 0 then the upper bound of 1 is also the maximum, But if we exclude it then again the upper bound is never reached and the set has no maximum either.

An abbreviation of british slang expression, common from about 1920s to 1970s. Right ho. Meaning I acknowledge what you have said and will carry on on that basis.

Very quickly before I head for the bank Part 3 of Callen Thermodynamics and Thermostatistics pages 455 - 471 Callen goes through modern interpretation of the quantum angular momentum rules via Noethers theorem (symmetries), Goldstone's theorem (broken symmetries) and gauge symmetries in relation to accessible and inaccessible microstates of a system and the state space of a system. The quantum rules forbid certain transfers of angular momentum which leaves ortho and para hydrogen as essentially different gases in a mixture.

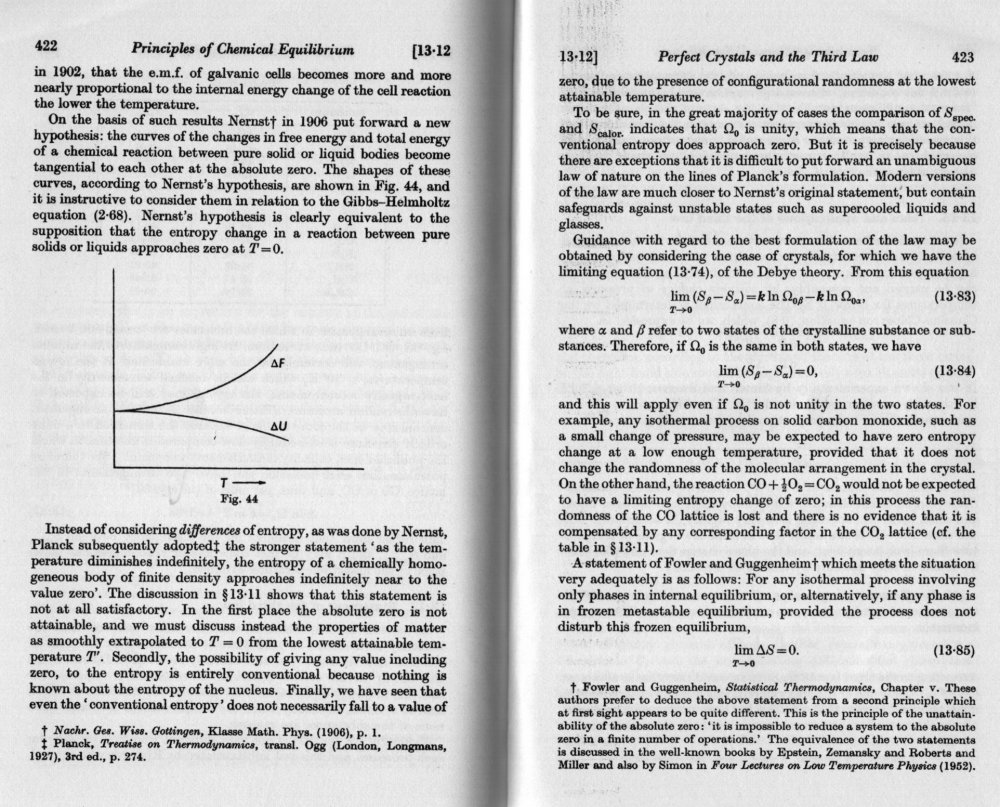
Glad it worked out for you! It was late and I was rushed last night. One of the very first books I bought at university back in 1968 was Denbigh's Chemical Equilibrium. He gives a much wider treatment of these effects both from a fugacity/Chemical Potential point of view (P1`22 - 132) and also form a statistical/calorimetric entropic point of view. Here are some pages of the latter which may be of interest since they cover a much wider range of gases that just hydrogen. The note at the bottom of p420 refers to Glasstone - an earlier work from 1940 - on page 588 My 1951 second ed has that material at the beginning pages 94 - 97 entitled Ortho and Para States. This may be more accessible for you as it is american. In deference to your opthalmology I have increased the scan deoth, although it means a larger file size. Yes I agree, the standard chemist's method of avoiding mechanical mechanisms is to go the least energy/ least action route. Another good reference is Wilson Thermodynamics and Statistical Mechanics 1966 Chapter 6 Specific Heats p 139ff 6.12 The Rotational Specific Heat of Hydrogen

No apology needed. If it is really inadequate the please do speak up. But do you realise that ScienceForums offer the full sized scsn by clicking on the pictures ? In my browser (firefox on and old XP Dell) this opens a new browser window whcih you can zoom to full size.

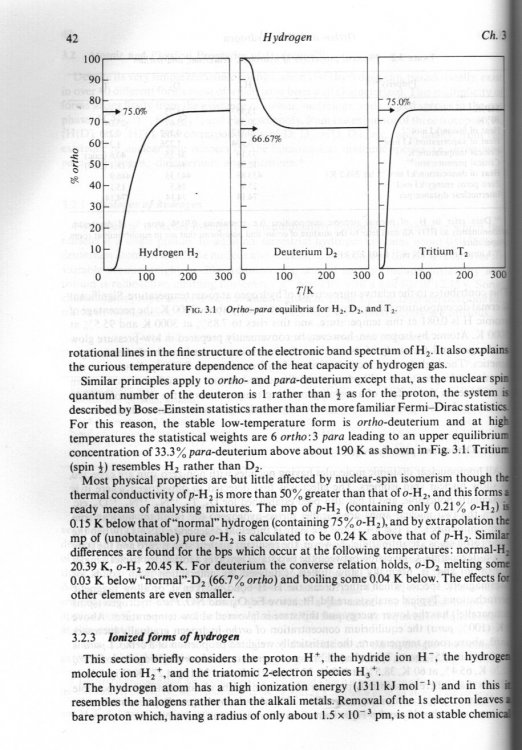
Here is some more information on Ortho v Para from Greenwood and Earnshaw Chemistry of the elements. Sorry for the quality of the scan but it is difficult for this book as it has over one and a half thousand pages.

Easy, we are doing it all the time in the UK where much of the building stock is old. It is called renovation and/or repurposing. Relevance to what? You made a statement I challenged it with examples from elsewhere where property was being sold at below construction costs for a variety of reasons. I also clearly admitted that this may not happen in the US, although some here seem to want to limit the discussion to the US, such requirement was not contained in the OP as far as I can see. But if, as you say, you wish to limit your discussion to brand newbuild properties only then the suggestion is that this build would be well away from existing cities and presumably on cheaper land, which is much more plentiful in the US than in Europe. I have also indicated that what we call 'planning gain' in the UK significantly adds to the total cost of newbuild. Again I don't know its fraction in other countries.

I see no maths, physics or science in the OP, just a lengthy blog sprinkled with a few scientific words and some non scientific ones. Plus a lot of advertising for some book or other. Plus a misunderstanding of the meaning of the quotation from W Pauli.

Genady and Lorenz have made some good comments but perhaps I should answer your question more formally. The line segment does not change its geometry - you misunderstand. Lines, line segments and numbers are all three different things. Lines and line segments are geometrical objects. Numbers are not. The real number line is a representation of all real numbers, placed into one-to-one correspondence with the real line as an assembly of points. There is no other similar correspondence with other types of number. We do this because it is a useful way of visualising things, especially as a lot of geometry is taught before any of the higher mathematics necessary to fully appreciate the comparison is taught. The correspondence goes all the way to 'point set theory' where the elements of a set (also called points) can be one of three types. Interior (also called accumulation points) , boundary or isolated. Genady has already described two of these, though he called a boundary point an end point. A set which includes its boundary points is called a closed set. A set which does not include its boundary points is called an open set. An isolated point is both closed and open. As regards line segments, a line segment has two boundary points and is called an interval or line interval. An interval can be open or closed, but since it has two boundary points it may include one and not the other and we either say the interval is half open or half closed. The whole real number line is open. The line segment or interval from say zero to plus infinity or minus infinity is half open. The interval from zero to say 2 is closed if it includes both 0 and 2 and open if it includes neither. These concepts are very important when you study limits and calculus, so they have their own special notation. Here is a diagram, showing the geometric and algebraic representation of the types interval (0,2) the rounded brackets are the general form when the type doesn't matter.

You specified construction costs. No it did not. It is even debatable whether central government ever had the right to cause them to be sold, since they did not pay for them in the first place. Where did I say any of these were new ? All houses need to be constructed at some point in their history. As a matter of interest some blocks of flats were sold in the north of England at £1 (I think the first was in Liverpool) for a whole blockbecause the local authority which had built them and actually owned them could not afford to upkeep them any more. I do think, however that your comment about the cost/worth of things is extremely poignant however. It just doesn't cover all bases. Also it is worth pointing out that the value of a property - as reflected in its current sale price - is hoped by the owners to be greater than their original purchase price, whether they just bought it or actually built it, but may end up being less. And that is called a free market. Yes I totally agree we have the means, but I would add not the will. +1

Well you would be wrong. We have already discussed the €1 houses in Italy. But Mrs Thatcher did exactly that with "The right to buy scheme" , which was only fairly recently ended in the UK. I don't know enough about other European countries to comment further in detail on them. And you still haven't confirmed whether you are including land costs and planning costs in your costings. It's the attitude and high anti-objectivity of the smart assed quips I am objecting to. Well I most certainly call this distortion of what I actually said cherry picking with the implication very clearly being that I want to claim it is " Their fault". Yes, that's a phenomenon - not the biggest problem, but one that's easy to cite by people who want to prove it's 'their choice; their fault'. Here's an article on the subject: I think it is such a shame that this thread has become simply a vehicle for those who want to hurl all embracing mud at anyone who want to objectively, and dare I say it - scientifically - unpick what is a very complex and in some ways sad situation. What is a homeless person ? I came across someone recently whos is technically homeless, (Of no fixed abode) but actually lives in a quarter of a million £ boat and runs a fleet of vehicles. I know that is an extreme case and plenty of truly homeless folk would jump at the chance to have a consistent roof over their heads. But I don't see how solutions can sensibly be proposed or enacted without starting with a proper analysis of who the homeless are, where they come from and why they are homeless. I know they are not one group to be lumped together but a hugely disparate lot. Nor am I holding UK experience out as any sort of paragons. I have already cited the grossly outdated and unfair vagrancy acts. But there are also many good goings on here and they should also be put forward. For example the Big Issue scheme has been said by many users to provide that sense of personal dignity and worth that allows or has allowed sellers to climb out of their difficulty by their own efforts. We had a seller in the South West who was well known and respected for a decade, who raised tens of thousands of £ for charity, yet chose to live in hostels for the homeless, moving round the SW. I know he finally quit and bought a modest property of his own. I repeat the situation is vary very complicated.

I think cherry picking from someone else's post should be beneath both of you. iNow I was responding to a point purely about resources, including cost. Peterkin how many UK homeless have you actually met to discuss their situation with ? And how familiar are you with UK vagrancy laws ? Both of you I have not in any way said nothing should be done. Quite the reverse if you bother to read my entire posts on this subject. There are, after all, precious few of them.

I didn't see an explanation from @Alex_Krycek to questions about the distinction between homeless people and homeless addicts. Nor a response to my own questions. Different problems require different solutions. Yes I agree in principle with CharonY but it may be worth noting that in the UK the vagrancy laws have not been repealed as our elected representatives have far more important squabbling and finger pointing to do than tidy up centuries old archaic legislation. You can in principle in the UK be prosecuted it you go out with no money in your pocket. These same laws require 'vagrants' to move on after a certain number of nights in any one place. These regulations are more rigidly enforced. So how is a homeless person supposed to return to normal, get a job and settle back into the community ? No one here has yet raised the issue of whether the homeless would actually take up social housing af any description. Again UK experience is that a significant % will actually prefer to remain homeless and 'free', because the cost to them of conforming in any type of available accomodation is too high. Finally I highlighted the difference between the US and Europe, in that the US land prices and palnning regulations play different roles in the 'cost of construction' - I didn't get a response from swansont on this.

The slip was too good to miss. Especially as the original proposal doesn't seem to have many (any?) backers for a variety of paractical, moral, social and legal reasons. Sadly nor has it had many admissions that there is a serious problem which I thought was clearly laid out in the OP, although I do not agree with the proposed solution. It is a pity that this thread has become rather entrenched hard line.

I didn't know it was random ?

Actually I wasn't suggesting that. Europe also suffers from this problem, though I have not seen any statistics to show the crime rate of homeless addicts is worse than many other sectors of the community. I am merely challenging swansont's assertion about construction costs. What do these include ? Interestingly there are quite a few do-it-up programmes on UK TV at the moment. One is just running a series on these €1 properties. They bought one (two actually) and have been doing them up.

In the US maybe. But I don't agree that it applies in more heavily populated Europe.