studiot

Yet again I have wasted my time and effort (and money buying windows 10) trying to reply honestly to a thread. I prepared this reply but when I submitted it it all disappeared again. I was able to recover it, but it disappeared 3 times in a row, although you can see from the screenshot that I was allegedly logged in at the time. For one of those tries, I tried relogging in but it still happened. Furthermore now I am logged in I thought adverts wer in general suppressed, not covering a significant proportion of the users screen ?

Did you check to see if the rules or ethos of this forum has changed since you last posted in 2011 ? At that time I note you posted some pretty decent Physics in accordance with our discussion rules. So what is your thread all about please ?

OK so as always the answer to you basic question can be as simple or as complicated as you wish. At the very simplest, yes there is complete demarcation between hardware and software. However that view will not get you very far. The most common model is usually called the layer model. This comes in various amounts of complexity ie more or fewer layers. The layers are usually portrayed in a vertical heirarchy. The simplest is the two layer model , with 'hardware' at the bottom and 'software' at the top. The all important idea is that there are predifined exchange parameters which are passed from one layer to the next. All communication between layers is by way of these parameters. Layers do not have direct communication with or control of other layers and can only communicate via these parameter channels with the layer immediately above/below. The reason for this is that the 'software layer' does not need to 'know' what is actually in the hardware layer. It could be switches, transistors, light bulbs, charged/discharged capacitors or it could be something non electrical at all. My flatmate in University did his final year project building a fluid logic hardware layer. One more generalisation and that will be enough for now. All this is of no use without the traditional 'black box' theory. You must have means of input and output otherwise you have a system that just sits there and contemplates its own navel. So I favour adding a horizontal direction to the model to account for input and output. If you find this worth pusuing, we can use the models, building up complexity, to look at your other questions about interactions and the nature of input and output.

Having dried my thermometer out I can report the following measurements Lenovo M8 tablet Battery 5000mAh reported power idle 0.5W, loaded 4W. Charger 2A usb = 10W Cover wallet constructed of leatherette covered card. Screen exposed, rest covered. Ambient temperature 23 C Tablet working temp at 40% charge 26.5 C, working on battery alone. Tablet switched off After 1 hour tablet cooled to 24.2 C Charging started 1/2 hour after commencement of charging, tablet @ 28.5 C 1 hour after commencement of charging, tablet @29.9 C 2 hours after commencement of charging, tablet @26.9 C 3 hours after commencement of charging tablet @ 28.5 C Reboot charge still connected charge 99% 3.5 hours after commencement charging tablet @ 28.5 charge 100%

Hawking, via Moontanman, his joke in the jokes thread is rather good too.

Here is the Wiki article on the subject of police doppler radar guns. https://en.wikipedia.org/wiki/Doppler_radar

Isn't all this talk of boilers off topic ? After all how many toilets have boilers ? I remember most work vessels in the 70s and 80s in the gulf using salt water to flush the toilets. Readers, may have come across the fictional character, modelled on Nelson, called Hornblower, treating himself to a daily sluicing in sea water (hand) pumped by the ratings on his ships, even in the Atlantic winter.

There are many sorts of slang. One not mentioned so far is Cockney Rhyming slang.

I wondered that and agree. Here is the modifed spreadsheet

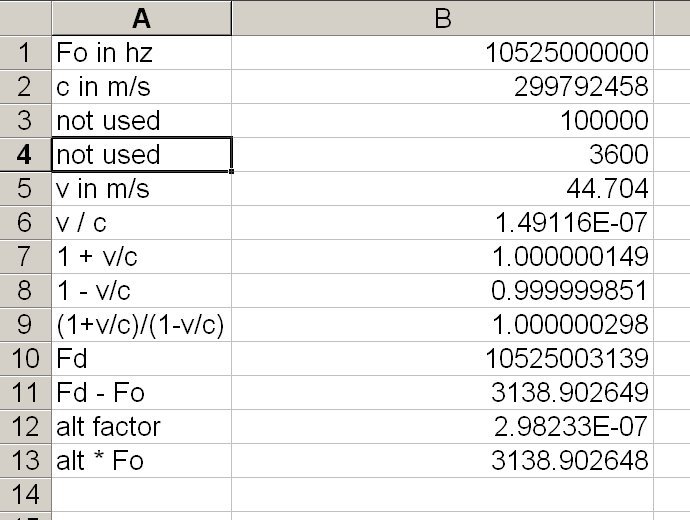
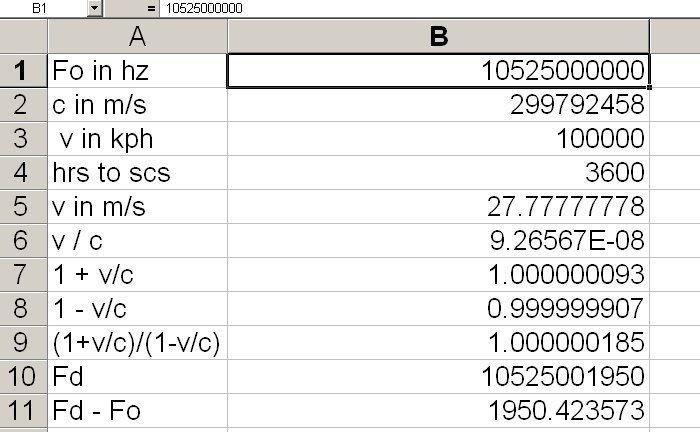
I agree that this would be the best Excel can do, and Excel is the best way I have for handling multidigit numbers. However since wee are talking about the difference between the last four digits to two eleven digit numbers, not to mention the loss involved in the quotients, there will be a lot of variation depending upon calculation method.

I made it 2328

Suggestions for using AI Combined with suitable human oversight, monitoring and controlling dangerous situations, places or activities such as prisons.

Surely you are looking at this all wrong because you should only allocate one axis per dimension. I'm sorry but although you quoted my previous technical comment, you made no response to it, instead taking the opportunity to promote another wall of woo. I have reported this for being placed in the wrong sub forum so I suggest you read the speculations special rules and contact a moderator if you need to.

What a pity you didn't simply ask how I came to my answer. If we try to substitute x = 0 into the given expression we find [math]\frac{{{2^x} - 1}}{x} \to \frac{{1 - 1}}{0} \to \frac{0}{0}[/math] Which we know we cannot do. But the situation is remedable as we can apply l'Hopital's rule thus [math]\frac{{\frac{d}{{dx}}\left( {{2^x} - 1} \right)}}{{\frac{d}{{dx}}\left( x \right)}} = \frac{{2^x}\ln 2}{1} = \ln 2 = 0.693[/math]

0 never 'equals '1 There are number systems without zero, it it not necessary for all number systems. From what you say you have obviously met some simplified explanation of the development of numbers and let your imagination run riot. The proper development of numbers is a very important and interesting (to some) subject in maths. We can discuss this properly if you like. I'm sorry but the rest of your post is just a kind of numerology, it is not science. Furthermore your 'stability' values fly in the face of direct observation. You should look at the 'packing fraction curve' ; Iron is the most stable element.

If you have your phone or tablet in a protective case, additional to the tablet itself, does anyone know or have any data on how safe it is to leave the device in the case for charging or should it always be removed ?

Thanks. Yes I have often collected quotes from various back pages by methodically going through and adding them to the imput box. Then moving on to another page and immediately clicking in the now empty input box at the bottom of the page which restores my previous collection so I can add to it.

I must say you seem to have a very deep interest in this subject, far greater than my own, as you keep referring to people and things I have never heard of. If you don't like it, why bother ?

Your reply may be relevant to many things, especially since they are interlinked. However I am sorry to say that I still am no wiser as to what you are saying. Pewrhaps it would help if I observed (as I have dome several times in the past) that there is nothing you can say in Mathematics that cannot be said in plain English, the converse is not true since there are many things you can say (express) in English that cannot be said mathematically. Is this what you are alluding to ?

test test test Many thanks for your concern. As you can see from my test it is working now. I think I will blame it all on Dave - he was, after all , lurking about the time it happened. 🙂

OK This is useful. Yes f is a function. That is it is a whole set of values of y each one corresponding to a value of x. Important features of functions are. Each value of x must correspond to one and only one value of y However many different values of x may correspond to the same value of y For instance the constant function y = 3 makes y to be 3 for each and every value of x. The whole function is the whole set of pairs of values, one x and one y in each. y = f(x) refers to all the pairs (x, y) and may represent a geometric curve. If the function is not to broken up it may be 'differentiable'. This means a second function called the derived function or just the derivative may be obtained from it by a process called differentiation. Thus the derivative is a function, just like its progenitor. The integral on the other hand is quite different. To integrate means to perform some sort of sum. Indeed the symbol is a stylised Gothic S. When you perform a sum you add things up and come up with a number. A single number. Luckily there are some formulae for performing this sum, but as Genady has already said, there is no general formule. The Fundamental Theorem of Calculus also comes to our rescue when we want to find these sums ( hence the link to area, volume and many other things) I called f' the 'primitive' which gives rise to the derived function - You can also use the term 'antiderivative' if you wish. This is really wonderful news because it tells us that the number we want - the sum the integral represents - is the difference between two numbers, the value of the primitive at each end on the region. I say region because the simple formula integrates (sums) along a line but the region may be a line an area a volume or more. A further comment looking ahead. Finding the primitive allows us to 'solve' differential equations which are equations containing both algebraic functions and derivatives. such equations arise quite naturally in just about every corner of science and engineering.

Exactly what I would expect your elementary Dummies book to say. So can you explain it further, what do you think f is? What do you think an integral actually is, when you say 'you are finding the (definite) integral....' ? What are you expecting to find ? These are not trick questions, they are meant to help you understand when I explain more fully. This explanation will include the reason I am putting the word definite in brackets. By the way the (definite) integral is not necessarily an area, though it can give you various area with suitable processing. For example the (definite) integral of sin x from 0 to 2pi is zero so it will give you nothing at all.

Well thanks for that. It is certainly non functional for me atm. All I did was test some Tex in the sandbox. Gosh that lot came up when I came to type in a reply, after entering your quote into the box. Weird. Anyway I would be very grateful if you could point me at any Firefox settings I can look at in W10

Consider the following Let [math]y=\frac{{{2^x}-1}}{x} [/math] What is y when x = 0 ? Clue it is not 1 it is about 0.693

[math]\int_a^b {df=f(b) - f(a)} [/math] Can you say what this means to you please ? It is known as 'The Fundamental Theoem of Calculus'.