joigus

Good one. Here's the catch: (my emphasis on OP's source) Nearly a 100 years in the books. And still people, when in doubt between reality and causality, would rather sacrifice the latter. It is reality that is dead as a sharp concept, even though it is a very good approximate one. This goes to show how adhesive the concept of classical reality is: "It's either this or not this" is harder to give up than smoking.

That's an outstandingly good question IMO. I know inverse problems in physics are notoriously difficult. Eg, the inverse-scattering problem: Given the scattering properties, find the scatterer. What you're proposing, in terms of scattering problems, would be: Given any scattering, can I always find a scatterer that does it? My guess would be no too. That you can always find a T that does it, even though you might have to make it un-physical. But I cannot go beyond the guess at this point.

Yes. Scale can dilute our delusions. It shouldn't should it? Einstein seems to have been of the same opinion. I find it very difficult to disagree with that. The most likely candidate to smooth things out is, of course, quantum mechanics. And Genady is very hard to win over, probably because he lives on an island.

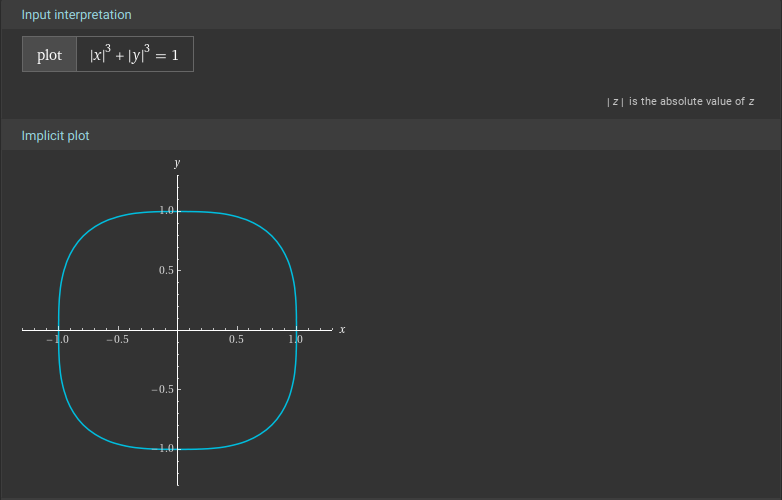
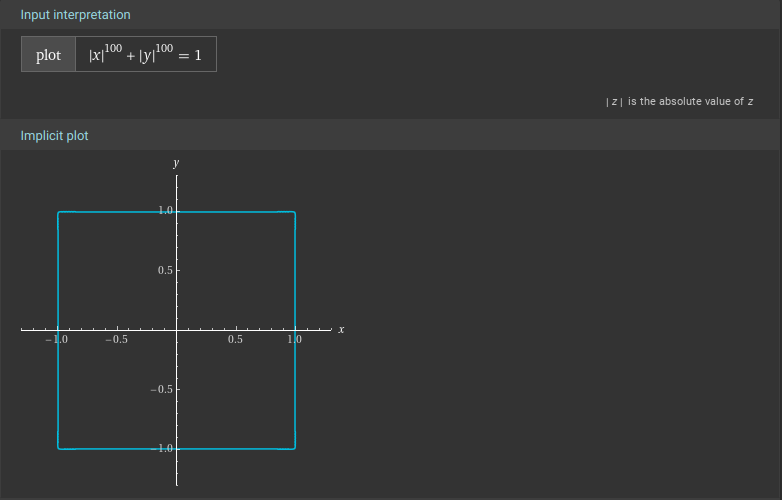
The argument that always creeps in is that, looks (and is) smooth enough, while, doesn't so much, although it's equally smooth. It's just that the curvature at the corners is enormous as compared to scale 1. These are called squircles, btw, and they're fascinating.

I always use pressing Ctrl+hyperlink, as suggested by Swansont. Fast.

Amen OP confused "theory of everything" with "everything I think is a theory".

OK. Then the Wikipedia article needs editing, because it's very confusing. It explains nothing of that. Not a thing.

Sorry I missed this. There seems to be a correspondence between one and the other, right?

Here's what I mean: According to Wikipedia, the definition of LCT's is, \[ X_{(a,b,c,d)}(u)=\begin{cases} \sqrt{\frac{1}{ib}}\cdot e^{i\pi\frac{d}{b}u^{2}}\int_{-\infty}^{\infty}e^{-i2\pi\frac{1}{b}ut}e^{i\pi\frac{a}{b}t^{2}}x(t)\,dt, & \text{when }b\ne0,\\ \sqrt{d}\cdot e^{i\pi cdu^{2}}x(d\cdot u), & \text{when }b=0. \end{cases} \] So it's just an integral transform acting on the time-dependent part of the position-variable representation of the total wave function. IOW, this transformation does not depend on colour, electric charge, weak hypercharge, spin, or any of that. Nothing! It doesn't even touch those indices. How can it provide classification into irreducible representations according to colour, electric charge, weak hypercharge, spin and all of that? I don't see how it does, and I can't picture any way in which anybody can tell me how it does unless they have a theory, as promised in the wikipedia article: What theory? Where is the theory? Does anyone have a theory to explain this utterly unbelievable statement that a group acting on one space helps classify objects defined in another (completely unrelated) space!!!? I know about Cartan, and Gell-Mann matrices, and unitary representations of compact groups. I know all of that. But it doesn't even begin to address any of my concerns about this.

For a whole bunch of good reasons! Mm... Not really. I'm very familiar with \( SU(2)/\mathbb{Z}_{2}\cong SO(3) \) and \( SL(2)/\mathbb{Z}_{2}\cong SO(3,1) \) and their algebras, as with some non-unitary groups. But it is one thing to decompose groups into factors and quotients and do the analysis in terms of Dynkin diagrams, central charges, Casimir quadratics and what have you, and quite a different thing is to state where these groups become relevant and why. And what they help to break apart and study. For example SU(2) can be said to embody how elementary particle "see" rotations in space (example: spin), or... it can also be an internal symmetry group that tells us nothing about space and just refers to abstract directions in the Hilbert space (example: hypercharge). It's still a mystery to me how parametric transformations in the "space" of energy and time (LCT's) is telling us anything at all about transformations in a completely different space (the space of colour, hypercharge, electric charge, and so on). I fail to see how even spin is included in the package. And I'm not any the wiser now. But it's perfectly possible that I'm just too rusty on this, so my apologies in advance if that's the case.

I find it a tad peculiar that the multiplets of the standard model are obtained[???] (correctly AFAICT) from this 3-parameter group that only acts on the frequency-time plane. Really? How does the E,t plane "know" about parity? The multiplets displayed there are sure those of the standard model. And the fact that electrons are called "negatons" doesn't bother me too much. But where do these "boxes" come from? From this group whose only motivation is to generalise and unify Fourier and Laplace transforms, as well as other reparametrizations of the phase? I suppose Wick rotations can be found accommodation there too... I don't know. I've been looking at the more readable page on LCT's, https://en.wikipedia.org/wiki/Linear_canonical_transformation And everything seems nice and dandy until we get to this table with the claim, "a" theory? What theory? This suspiciously sounds like a non-properly-curated addendum to the previous wikipedia article by some people intent on self-promotion. I could be totally off-base, but I find the last paragraph of the wikipedia article very suspicious even though the table is that of the SM. They haven't shown to me to any degree of accuracy or plausibility that the table can be proven from the representations of the LCT. Besides, the LCT is 3-parameter group. The standard model, OTOH, is what SU(3)xSU(2)LxU(1) --> 8+3+1 internal + spin Only counting the compact-group (quantised) degrees of freedom. It doesn't add up in my mind. How did you come across this? What is you interest? Can you tell me more?

I don't think so. AAMOF, ideas like "we live in a simulation" or panspermia sound to me dangerously close to trying to revive the idea of an intelligent creator, but with an aura of scientism about it. All of them (and the ones to come) equally vulnerable to the infinite-regression argument: Who simulated the simulators?, and Who seeded the seeders? etc.

That's from Life of Brian, if I'm not mistaken. I testify to the fact that the teleological argument has been receiving some attention lately. More of a cardiac massage, IMO.

On my part, it's OK. Those aren't bad questions necessarily. Any imprecision is understandable on account of the difficulty of the subject. IMO Mordred's answer was spot on and succinct. I have little to add to what he said. You seem to be bothered by the presence of fields in the geometry though, and that's fair enough. In pure geometry we don't have this arrowy structure we call fields. On top of that they have an algebra of creation and annihilation, and they are complex (have an imaginary part). Those are quantum fields and they seem to go beyond the scope of geometry. Does space-time emanate from the field, or is it the other way? Nobody knows. Maybe there was an eternal inflation scenario, as some models say, and scalar fields gave shape to everything else. It's, as Mordred said, speculation. Highly educated, yes, but speculation after all.

I suppose what @MigL means is that differential geometry is no longer applicable. There is no point closer, and closer, and closer still to a given point. There might be "quantifiable relationships between distinct objects" but not of a geometric nature. Or there might be no distinction of objects. Or... I suppose when you say "objects" you mean points? Maybe the quantifiable relationships are something like entanglement, but that's not really geometry.

No, we can't. Modern humans diverged into their different phenotypical varieties, if you will, about 70,000 ya. while, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9374477/#:~:text=The divergence time between the,camel was different from the around 6 million years ago¹ African and Asian elephants diverged from a common ancestor around 6 million years ago¹ and are two distinct species that differ in many physical attributes². For example, Asians have small round ears and twin-domed heads while Africans have large ears and rounded heads².Apr 25, 2023 Modern humans are in fact genetically closer together than most other species. One of the few species that are much tighter together than us is the cheetah. Have you heard of the 70,000 year old bottleneck due to the Toba eruption? Cheetahs are eve much closer together than us because their bottleneck happened only 10,000 ya. All this info you can find on the internet. You only have to bother doing so.

No. They tend to be female. Can you be constantly wrong in a little less inflammatory way?

I was joking. I'd share a beer with you two too. Certainly possible. I prefer to think in terms of how the character of Muhammad has been construed through time. Like what influential people that came after him did with his figure, as well as the early offshoots of Christianity at the time he is supposed to have lived. Don't forget it was Waraqa ibn Nawfal, a Nestorian priest (Christian), who authorised him as a prophet.

That I find highly illogical. I think you got the song wrong. This would have made a lot more sense, https://www.youtube.com/watch?v=hFDcoX7s6rE

I haven't, but I'm very interested in anything you might have to say about it. Not to say I'm not enjoying the discussion on local realism and the concept of reality. (As well as the ongoing intellectual feud between Moontanman and Dim.)

Yeah, hunter-gatherers are the problem. Sigh

I shy away from worldviews (try to), even though sometimes I can't help getting tangled in them. There are too many obstacles, some of them really thick, to acquire any kind of a vantage point. And the individual perspective is only too limited. I see a piece of landscape from where I stand. That's all. Besides, there are already too many Manichaeans out there, preaching with too loud a voice. I don't want to be that person. I must side with Genady here, but as a dream perhaps. That some day mathematics, logic, and similar tools of analysis can tell us what this or that pattern does in the great scheme of things. As for the rest, such tools will hopefully tell us why and what in the world cannot be understood on account of logical/semantic incompleteness. Mathematics is so... dispassionate. Atheism is not a worldview, btw, as far as I can discern. It's more of a 'what do you mean by that' attitude the way I understand it.

Also, \( \nu \) in \( E = h\nu \) is the Greek letter nu, while \( v \) in DeBroglie's relation \( \lambda=h/mv \) is the Latin letter v. Could that be related to your problem? IOW, one is the frequency in Hertzs, while the other is the speed.

I'm no expert here, but feedback mechanisms in biology are so frequent that I think pointing to the presence/absence of a certain chemical as the cause of an illness (or of any other process for that matter) is probably not the way to go.

It's Sagan, of course. And after that, Sagan. The poetry, the music, the absolutely unfettered passion for understanding it all that cannot be muffled in any way. The Cosmos is all that is, or was, or ever will be... And I was immediately and unconditionally engaged for the rest of my life. As to the rest of them, I can't help but feel they've been built as marketing products in a way, probably through no fault of their own. I agree with exchemist that Hossenfelder means business more than any of the others. Sorry for the mixed metaphor.