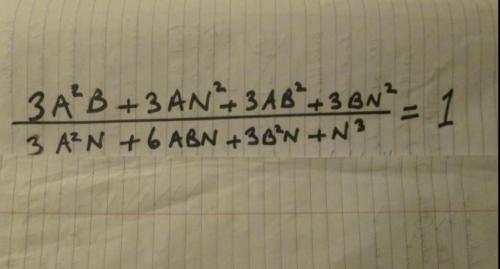-
Posts
622 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by Joatmon
-
I'm a bit puzzled scanning through this thread but there are a few points I'd like to add. The first is obvious - Right angled triangles have sides that comply with Pythagoras theorem. The second, once you have your triangle you cannot multiply different sides by different amounts - in effect you would be altering the shape of the triangle. Each side must be multiplied by the same amount. Lastly such a triangle represents either constant forces or if forces are changing it can only represent a particular instant in time. I'm retired now but my speciality was electronics and our main complication concerned sinusoidal forces (voltages) where appreciating the difference between instantaneous value and a steady state equivalent was necessary. I don't know if this helps, but it's my two pennyworth
-
OK, I'll be the gullible one! If we can assume that one, and only one, of the boxes contain a correct answer then the percentages shown have nothing to do with the question. If we had asked four people to choose the correct location of the answer to the next question and they each choose a different letter -A, B, C, or D then surely only one will be correct? Each individual will have had a one in four chance of getting it correct. What am I missing ?
-
As I understand it one of the golden rules of the universe is that you never get something for nothing. I would therefore think that if anything is happening in the warmer space that takes any energy at all then that energy must come from the aluminium supercooled ring. Your idea seems to be rather like the idea that you could drive an electrical generator from a wheel of a car and feed it back to an electric motor and have transport for nothing. I wonder why you would need a massive aluminium ring - if the idea works then I suppose the mass of the ring is immaterial. Another way of looking at it is to consider whether you have created a perpetual motion machine.
-
Although it can't carry energy or information at that speed I'll mention, just for fun really, that phase velocity in a rectangular waveguide travels along the waveguide with a speed greater than light. I remember the incredulity with which the fact was met when first introduced to us when radar students.
-

Delete All of My Posts Please!
Joatmon replied to Winner568's topic in Suggestions, Comments and Support
I'm not a legal expert in any sense but all I know is that quotes such as follows have the owner of at least one forum worried enough to grant such requests just in case there is a post somewhere in the "conversation" that could be claimed to breach data laws:- “‘personal data’ means any information relating to an identified or identifiable natural person (‘data subject’); an identifiable natural person is one who can be identified, directly or indirectly, in particular by reference to an identifier such as a name, an identification number, location data, an online identifier or to one or more factors specific to the physical, physiological, genetic, mental, economic, cultural or social identity of that natural person”. In this particular case with only three posts I can see that it is quite easy to check. Just saying........... -

Delete All of My Posts Please!
Joatmon replied to Winner568's topic in Suggestions, Comments and Support
If you are subject to UK law I'm not sure you can refuse to remove personal information. Among the wording is "Make it easy for people to withdraw consent and tell them how." I am a moderator on another site and it is for that reason we allow all data we hold on a member, including their posts, to be deleted if they so request. -

Why do we need vacuum tubes, transistors..why not just use DC?
Joatmon replied to Elite Engineer's topic in Engineering
Question asked - Why even have the power source (wall outlet basically) connected to the VT, and just hook up the power source up to the computer directly, Simple Answer. Wall sockets provide relatively high voltage alternating current, computers run on low voltage direct current, as do most electronic circuits. You need something to reduce the voltage (a transformer) followed by something to change the alternating supply to direct current ( a rectifier). The rectifier back in the 1960's would have used one or more vacuum tubes (thermionic diodes). With the coming of transistor technology the diodes would be replaced by semi-conductor diodes (PN junctions). Later still the development of silicon based devices such as transistors and microchips allowed ever more complicated circuitry to be developed that would hold the low voltage circuit supply steady under different loads and a range of input voltage. We now call a package that contains the three elements(voltage reduction. rectification, stabilisation) a power supply. It usually is a small black box that sits between your wall socket and your computer. -

Fermat's Last Theorem with hardly any Mathematics
Joatmon replied to Joatmon's topic in Analysis and Calculus
Thank you for giving this thread your thoughts, it is appreciated. I must think about what you say about the infinity of numbers that exist in the infinitely small space that exists between each of the infinite set of numbers. My feeling is that when it comes to plotting graphs there won't be any surprising jumps - just a continuing of a smooth transition. For example it is surprisingly easy to "show" the square root of two on a plane surface and it fits into the general scheme of things. BTW the link you gave for Cantor's Diagonal Argument took me to the wrong place, but google soon sorted that out so I'll have a slow think about it. Well yes, concerning the cosine wave - I wasn't bothered about that as they have the same shape and can be plotted using the same data. On phasor diagrams etc they are 90 degrees out of phase with each other but adding two cosine waves will produce another cosine wave so this doesn't affect my argument. I'm sorry my laziness put you off. As I round off this post it strikes me to mention that the sine function is a natural product of nature that is follows things like vibrating strings,electromagnetic waves and swinging pendulums. This leads me to conclude that regardless of any number system the progression is continuous and smooth. Anyway, thanks again for your time and your thoughts, I haven't given up yet on what is something of a hobby -

Fermat's Last Theorem with hardly any Mathematics
Joatmon replied to Joatmon's topic in Analysis and Calculus
Thank you Carrock for considering my ideas concerning Fermat's last theorem. Concerning the points you raise you can plot a sine wave by dividing a straight line of numerical value 1 by any number of fractions, comprise a table of the square root of each fraction and make these the points on your graph. In theory you could use an infinite number of plots for an infinite number of fractions. You can use this data to go up and down and then down and up to produce one cycle of a sine wave. That will cover all possibilities concerning Fermat's mention of integers. I don't understand the comment sin x cannot be greater than 1. I said that the maximum value of sin x was 1 and if all the fractions were multiplied by a greater number you would produce a sin wave with a peak value of that greater number. I'm sorry if my use of IMO put you off. Of course I would like you to look beyond that and let me know where you feel I have gone wrong if you see a misconception. That would be a real help. -

Fermat's Last Theorem with hardly any Mathematics
Joatmon replied to Joatmon's topic in Analysis and Calculus
I don't see a problem, but perhaps the point you raise was why Fermat stipulated integers, not irrational numbers. However if you could get absolutely accurate values for e and pi then the following would, IMO, be true:- One of the sine waves to be added would peak at e times 1 (sine 0 degrees), be e times .707 at 45 degrees and e times 0 at 90 degrees. The other sine wave to be added would similarly peak at pi times 1, be pi times .707 at 45 degrees and 0 at 90 degrees. If these two are in phase and added the resultant would peak at e+pi and if one is phase shifted with respect to the other the resultant waveform will have a lower peak value. When the resultant phase shift is the correct value it will be SQR(e^2 +pi^2). This will happen at a phase shift of 90 degrees. Therefore squaring each side of the triangle will produce a correct sum e^2+pi^2=(SQR(e^2+pi^2))^2. NB *707 is approx SQR(1/2) . -

Fermat's Last Theorem with hardly any Mathematics
Joatmon replied to Joatmon's topic in Analysis and Calculus
Perhaps I should have realised that someone might think he had a possible solution that was 1^n +2^n=10^n! I thought the point was covered in the first line. To be clear I should have asked the reader to also satisfy themselves that in all possible candidates for A^n+B^n= C^n, C will be larger than A or B and smaller than A+B. , -
Someone claims to have a whole number solution to A^n+B^n=C^n where n is greater than two. If they have the three numbers then they can form a triangle. This triangle will always have an apex (junction of A and B) which will be less than 90 degrees. Please consider whether you agree with this statement before proceeding! This triangle can be considered as a triangle of forces and from which a parallelogram of forces can be drawn. Using the parallelogram of forces both a vector diagram and a phasor diagram can be drawn and used as reliable tools for navigators and engineers of all disciplines. A phasor diagram can only be used for adding sine waves and they must be of the same frequency. By definition each point on a sine wave is a multiple of the square root of a proper fraction. (opposite divided by hypotenuse) If you plot a graph or create a waveform where each plotted point is something different to the square root of the fraction (say the cube root) you will have a graph that is not a pure sine wave. Only a sine wave has the property of adding two sine waves to make another sine wave. Any other shape of waveform or regularly repeating graph has to be considered as a group of sine waves of different frequencies acting together( fundamental frequency and harmonics). This is Fourier analysis of a waveform. So each frequency that makes up the waveform that is not a pure sine wave, requires its own phasor diagram, hence its own triangle, and you would need to analyse a full set of these triangles to form the final total. But it was stated earlier that a single triangle would suffice! The rather strange conclusion that I come to is that s each side of a triangle, where each side is an integer, is the square root of something and the triangle gives a correct addition of these square roots on a plane surface. Only triangles with an apex angle of 90 degrees will form a a phasor or vector straight line if all sides are squared. The case was made earlier that all triangles that represented A,B,C, in the formula A^n+B^n=C^n where n is greater than 2 will not contain a right angle. That all such triangles can represent a vector or phasor diagram on a plane surface and that the only chance you have of putting the vectors or phasors (which represent sine waves of one frequency) in line is to square each side. It will always fail to do so if the triangle does not contain a right angle. So the rather strange conclusion is that it is only possible to construct a triangle, where each side is the square root of a number. The the only way of using the triangle to represent a sum is to square the sides. If the triangle is right angled we get a correct sum and if the angle is less then 90 degrees we get an incorrect sum.. So, for example a triangle of sides 6,8,9 which seems to almost represent 6^3+8^3=9^3 represents two phasors separated by approximately 110 degrees, which provide the incorrect sum 6^2+8^2=9^2. I see this as strong evidence, perhaps even a logical proof, that Fermat's last Theorem is true by absurdum.
-
Perhaps any gap, or void that has been mentioned would be in the form of water vapour. This seems closely allied to cavitation on ship's propellers. https://www.iims.org.uk/introduction-propeller-cavitation/
-
Can't argue with that I guess that if I got a chance to play chess against a grand master I would jump at the chance and come back for more after losing. I suppose its a question of what one finds interesting or fun
-
That is true and also for other specific values of n. However, perhaps the source of the formula I gave might lead to a generalisation for all values of n. I admit that is unlikely but it is an interesting conundrum.
-
I think that sometimes a journey and its byways can be as interesting as a destination never reached. Also, I feel certain that there are a number of people in the world, such as me, who although knowing they are almost certainly deluded, think that there is just a possibility that there is still to be found a much more simple way of proving Fermat's Last Theorem than that produced by Andrew Wiles'.
-
I'm not surprised - if I have worked things out correctly then a whole number solution would lead to a whole number example of A cubed plus B cubed = C cubed. If it can be proved that there is no whole number solution then it can be concluded that there is no whole number solution to A cubed plus B cubed = C cubed.
-
I have reason to think that if A, B and N in the following equation are positive whole numbers then there is no solution. I would like either values of A, B and N which satisfy the equation or a reason why there is no solution. If you think it looks easy then give it a go - please.
-
Starting at a Texas University Well done my son, we're proud to see you're off to university. We've done our best to see that you have everything to see you through. You have already got a phone so there's no need to feel alone. On Facebook, Twitter and the rest are friends to help you when you're stressed. When you became a teenage buck we bought you your first pick-up truck; and in your eyes we saw the joy; a young man now, more than a boy. So now for university, here is a gift from Ma and me. A shoulder holster made to hide this deadly handgun by your side. We hope when your semester ends you'll be alive and making friends. Not lying on a blood soaked floor shot down while running for the door. (On August 1st 2016 it became legal for Texas University students to carry a concealed handgun)
-
(2*(6-(3*2)))/ (1*(8-(4*2))) should do it or if you would prefer it to equal 3:- (3*(6-(3*2)))/(1*(8-(4*2)))
-
Mercury must be high on the list. It is used in mercury arc rectifiers which work at high current and/or voltage levels.
-
An alternating current is accelerating and decelerating all the time.
-

Is it the Universe created alone? Yes or not? Only Yes or Not.
Joatmon replied to Enric's topic in General Philosophy
We seem to have drifted away from the original question of "Yes or Not". That being so I feel tempted to chuck in my two pennyworth:- Imagine that a scientist can lead a team into the discovery of how to make a huge black hole that could gobble up our present universe and thus create a singularity that explodes into a new big bang, and can't resist trying it out. Eventually the system might settle down to something like our present universe, life may start, intelligence may come from evolution and the idiot who led the irresponsible team might be given the a name that would translate as "God". Just a thought -

Is it the Universe created alone? Yes or not? Only Yes or Not.
Joatmon replied to Enric's topic in General Philosophy
I understand that some evidence has been found suggesting our universe has collided with another universe. This evidence, of course, suggests that our universe is not the only one. http://www.ibtimes.co.uk/evidence-multiverse-we-might-have-just-bumped-into-another-universe-1526526 -
Have you considered writing an ebook for Kindle (which can be read on a Kindle or any computer with a free Kindle App)? It is quite easy, with the method easily found on the web, and is free to produce. The only downside, and it's a big one, is getting it advertised. I have produced a book (albeit of poetry) and you can get an idea of what can be done - and what can be found on the internet if you click the link http://www.amazon.co.uk/Innocence-Erotica-Poetry-Anthony-McCafferty-ebook/dp/B00BVAKQLQ/ref=sr_1_1?ie=UTF8&qid=1448379046&sr=8-1&keywords=anthony+mccafferty