Everything posted by Genady
-
If Black holes slowly evaporate over time is there a point where they stop being a black hole?
I don't know. Occam tells me, it's nothing.
-
If Black holes slowly evaporate over time is there a point where they stop being a black hole?
Exactly so. A value of a function being undefined somewhere is often part of a function's definition. It does not break math or anything. A singularity exists, by definition A notion of a particle "being there" is undefined, by definition
-
If Black holes slowly evaporate over time is there a point where they stop being a black hole?
Nothing. The 4D-spacetime curvature becomes infinite. So what? The intrinsic curvature at the vertex of a 2D-cone is infinite, too.
-
Your thoughts on Neil deGrasse Tyson
From what I heard and read from him, I am sure he knows and understands this very well.
-
If Black holes slowly evaporate over time is there a point where they stop being a black hole?
Free entertainment. Even leaves one with a fuzzy feeling that they learned something.
-
Aliens from space (split from Time to talk about UFO's or now as the military calls them UAP's?)
Roadside Picnic - Wikipedia
-
If Black holes slowly evaporate over time is there a point where they stop being a black hole?
As mentioned in the link given above, Since 1 Planck mass is approximately 21.76 micro-grams, I've posted this:
-
If Black holes slowly evaporate over time is there a point where they stop being a black hole?
Sure. I thought rather that it is in micro-grams.
-
If Black holes slowly evaporate over time is there a point where they stop being a black hole?
A few grams?
-
Why is Argon Chosen for Double Glazing?
From my SCUBA diving days, I remember that argon was used for dry suit inflation in cold water diving because of its thermal insulation and non-corrosive properties as well as its low cost.
-
How does a physical system evolve under acceleration?
Yes. The time dilation does not happen at some event or events along the ship's worldline, but rather accumulates along the entire worldline. You can have a wild worldline with accelerations, decelerations, turning back and forth, etc., like this, for example: You divide that line into infinitesimal straight segment. On each segment, the proper time of the traveler is \[d \tau^2 = dt^2-dx^2\]. Then you integrate, \[\int{d \tau}\] to obtain the total time of the travel on the traveler's clock. Just a matter of calculation, see above.
-
How does a physical system evolve under acceleration?
It is wrong to assume that physical processes during acceleration are responsible for the time dilation. Time dilation is a geometrical rather than a physical effect. It is caused by the geometry of Minkowski spacetime. Let me describe the "twin's paradox" when nothing happens during an "acceleration". There is a clock located at 4 lh (light-hours) from Earth which is synchronized with the clock on Earth. Let's call this point in space, T. A ship moves with the speed 0.8c past the Earth. At the moment when a clock on the ship passes the clock on Earth, it is set to whatever is the time on Earth. Let's say, 10:00. The ship reaches the point T in 4/0.8=5 hours in the Earth time. The clock in T, which is synchronized with the clock on Earth, shows 10:00+5=15:00 when the clock on the ship passes it. However, the clock on the ship shows at this exact point in spacetime, i.e., as the two clocks are side-by-side, 10:00+3=13:00, because the time dilation factor for the speed of 0.8c is 0.6, and thus the trip to the point T takes 5*0.6=3 hours in the ship time. At the same exact point in spacetime, another ship passes the point T, going toward the Earth with the speed 0.8c. They grab the ship's clock and take it back to Earth. This trip back takes the same 5 hours in the Earth time and the same 3 hours in the ship time. So, when the clock returns to Earth, the clock on Earth shows 10:00+5+5=20:00, while the returned clock shows 10:00+3+3=16:00. Done.
-
How does a physical system evolve under acceleration?
This is how the "twins' paradox" is usually set up.
-
How does a physical system evolve under acceleration?
As you were writing that post, you were an accelerating observer, according to the equivalence principle. The ISS, for example, is a nonaccelerating one. Here are all your answers.
-
The equivalence principle and blueshift
I think you can figure it out yourself. Hint: compare with tidal effects, which exist on Earth but not on an accelerating spacecraft.
-
Intuitively, why doesn't always picking unpopular integers lower Probability of winning lotteries?
Here is my intuition. Let's assume that I artificially narrow myself to the range [N, N]. I.e., my range contains only one integer. Does it lower my probability to win? No, it does not. The probability is still 1/N, like that of everyone else.
- test
-
The predominant color of the flora and plant organisms of a planet in relation to the type of star it orbits and the wavelength it generates.
Hmmm... My blood is just dark green there. Not fluorescent at all.
-
My hypothesis to explain the difference between expansion mearements between James Webb & Hubble telescope AND ESA Planck satellite
This is factually incorrect. Observationally, the cosmic microwave background radiation is redshifted in one direction and blueshifted in the opposite direction. It is attributed to our peculiar motion relative to the cosmological comoving reference frame. Only after this peculiar motion is removed, the universe appears to expand isotropically.
-
do you believe demon possessions and fallen angels are real
I also am very far from being an expert, rather just a witness. In the case I've witnessed, specific environmental factor has made obvious a very serious form of schizophrenia, but then its signs could be traced back for years of misdiagnosis.
-
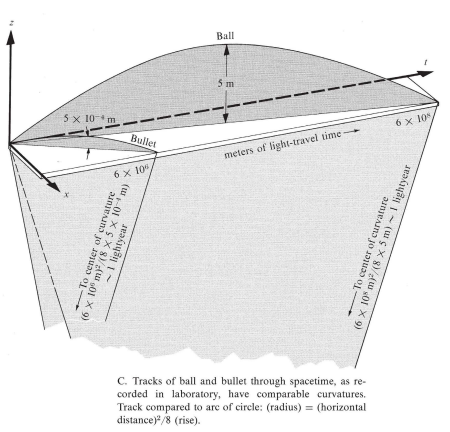
A different way of looking at the trampoline analogy
It depends on the symmetries of a situation. For example, a spherically symmetric case, e.g., Schwarzschild black hole, is usually visualized in 2D, i.e., temporal and radial.
-
A different way of looking at the trampoline analogy
-
I really need your help with some calculations
At the very far distance, the angle between light rays from the star becomes 0, that is the rays are just parallel to each other. Draw the picture and you will see what happens to the shadow when the rays are parallel.
-
I really need your help with some calculations
1 metre, 2 metres, 10 metres, assuming the shadow is perpendicular to the light ray.
-
A different way of looking at the trampoline analogy
You are spoiling my question in the post right above yours ... 😉