Genady

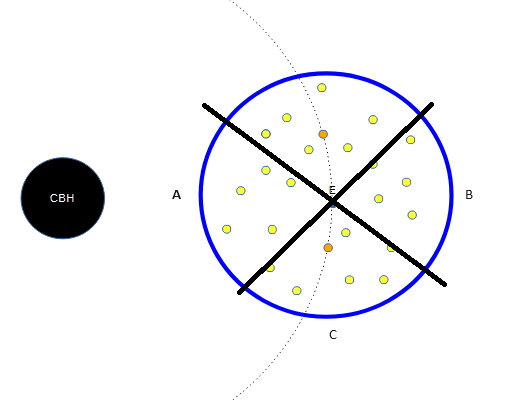
It is a mistake to think that only the bodies at the exact distance of the Earth would be accelerating toward the Earth and all the rest would be accelerating away from it. In fact, there would be two cones, A and B, where the bodies will be accelerating away from the Earth, and the 3D volume, C, where they would be accelerating toward the Earth: The relative sizes of A+B vs C depend on the angle of the cones, which depend on the distance from CBH. In case of the angle being 90 degrees, as on the drawing above, the volume of the two cones, A+B, is about 30% and the volume of the C is about 70% of the blue sphere. This means that in this case, about 30% of the observed supernovae would be accelerating away and about 70% would be accelerating toward the Earth.

These supernovae are not located on a line. If you see a supernova that accelerates away from the Earth, then looking in a roughly perpendicular direction you'd see supernovae which accelerate toward the Earth. The fact that the supernovae in all directions accelerate away from the Earth contradicts this model.

It is much more likely that more of them are located tangentially rather than radially, because there is only one radial dimension but there are two tangential dimensions.

However, objects located tangentially rather than radially from E would be accelerating toward E.

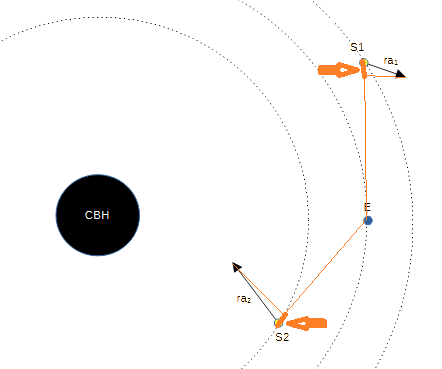
Yes. Why wouldn't you draw all four bodies aligned? If you did, S1 and S2 would certainly be accelerating away from E.

Because this is how "toward" and "away" are defined.

Both S1 and S2 in the drawing are accelerating rather toward the Earth:

My dogs certainly would. (Don't know about your diving experiences, but I 'communicated' with dozens of octopi in their natural habitat. The latter includes divers.)

Yes, in my own way.

The octopus saw divers making this thing and wanted the diver to finish it because it is currently useless, to the octopus.

If you want me to go on arguing, you'll have to pay for another five minutes.

No, they can not

Why?

What is "infinitely dense point"? No, it is not. No, we would not.

🤣

... ... The Monty Python's argument sketch comes to mind.

Is this combination of she/his intentional? I would hope so. Thanks again.

Just a friendly reminder: https://www.scienceforums.net/topic/132167-what-is-the-nature-of-our-existence/?do=findComment&comment=1246935

Downloading now. Thanks. Why didn't I know about it yesterday, the Bird Count Day here?

Thank you, @Eise. I'd try a different approach: are you familiar with, and if so, what is your opinion on PhilPapers: Online Research in Philosophy?

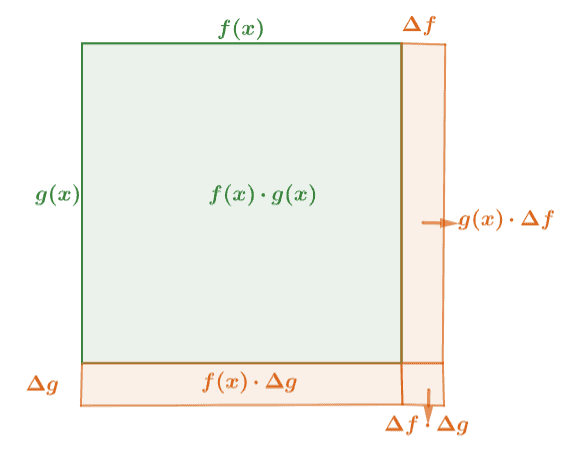
I didn't find it but since most Newton's derivations in Principia were geometrical, I assume that the product rule's derivation was geometrical as well. It could be as simple as this:

Thank you again. If I took that class with Agassi now, I'd have a lot of questions to talk to him about. Unfortunately, at that time I was too focused on my own wrong ideas related to philosophy of technology. While writing my previous post I learned that he died a year ago. He was very kind and very sharp.

Yes. And mathematics. Thank you. Just have looked at it in amazon. Have several concerns: 1. Although it technically falls into the range of "past decades", it is older than I'd like. 2. The amazon description says about the book's topic, "whether quantum mechanics gives a complete account of microphysical reality", which is not what I expect in case of "no philosopher today sees philosophy as a way to empirical truths". 3. $80 paperback, no Kindle version. Thank you. Some 35+ years ago I took (and successfully passed) a semester class in philosophy of science from Prof. Agassi in Tel-Aviv University. We went through a set of schools of thought. I would like to learn about new, later ideas.

I (not a scientist) am unaware of these changes either but would like to get a taste of them. Any recommendations?

They did not know what is wrong in their logic, and I pointed that out.