Daedalus

I'm not convinced that N170 has much effect, if any, on ones I.Q. score. Wikipedia states: The article by CNews, Staring at naked women makes you smarter: Study, is highly misleading and an example of bad journalism which demonstrates a misunderstanding to the nature of the study and its conclusions. The article attempts to justify public nudity by relating the increased electrical activity in the brain caused by viewing naked people to mental health and improved I.Q. Even though I have no problem with nudity and must confess that I enjoy seeing a beautiful woman naked , I feel that this type of journalism, even though it is fun to read, can cause more harm than good. Especially since the journalist is misleading the reader to believe that the results of the study suggests that viewing nudity will make you smarter. Perhaps the journalist is referring to our sexual I.Q. in that seeing naked people will raise our intelligence of the different shapes / appearances of the opposite and / or same sex (i.e. men and women might not be so self-conscious of their particular parts if they knew what everyone else looked like in the birthday suits) . I, of course, have no objections to being a part of your study Pantheory and would gladly help you develop experiments and gather data...

Pherhaps it has something to do with the following bolded remark from the article ; )

Mooey you make an excellent point. Unfortunately they didn't specify the number of participants that had one sexual preference vs. another. However, the article suggests that they did take sexual preference into consideration. Whether or not they made an attempt to choose a large enough group which contained a diverse spread of sexuality is unknown. It would seem as though they either are not listing the sexual preferences or did not conduct the study to initially consider the effects of varying sexuality. I stand corrected. They did list the method they used to determine sexuality. Unfortunately, they did not choose a balance between sexuality. They could've obtained any mix of sexuality and therefore their statement regarding the participants sexual orientation affecting levels of N170 is inconclusive: However, the statement suggests that the levels of N170 were different for those who are heterosexual vs. those who are homosexual and varying degrees thereof. A larger study would be needed which ensured the sexuality of each group of participants to validate the claim.

What I really want to know is if this truly makes you smarter in that your overall brain function speeds up for tasks other than looking at naked people. I have no doubts that our brain activity increases due to excitation and pattern recognition of viewing a naked person. But, can we really say that this activity is making us smarter and increasing our overall ability to think faster? I highly doubt this is the case because the article Michel123456 posted only talks about elevated levels of N170. According to the research article, male subjects are more interested in the opposite sex than women. Also, sexual preference "migt be modulating the N170 responses to nude bodies".

This one is actually quite easy, but I can't do your homework for you : ) Can you show us what you have tried so far and the results you have obtained? I or anyone else can then help guide you to the correct answer. I can at least give you a few hints in that you need the equation which defines position in relation to acceleration, initial velocity, and initial position as follows: [math]y=\frac{1}{2}\, a \, t^2 + v_0 \, t + y_0[/math] You should know the acceleration provided by gravity, [math]-9.8 \ m / s^2[/math]. You also stated the initial velocity, [math]39.2 \ m / s[/math]. Since you didn't specify an initial position, we can safely assume that both balls are thrown from the same height and you can zero out the [math]y_0[/math] variable and simplify the equation to: [math]y=\frac{1}{2}\, \left(-9.8 \ m / s^2\right) \, t^2 + \left(39.2 \ m / s\right) \, t + \left(0 \ m\right)=\left(-4.9 \ m / s^2\right) \, t^2 + \left(39.2 \ m / s\right) \, t[/math] Next, you need to know how to set up the problem. The key here is that both balls travel the same path except one ball is thrown four seconds later. This involves modifying the equation to account for the offset in time of four seconds for the second ball. Then, set the equations for both balls equal to each other to solve for the time their positions are equal. I'll be happy to help you out once I have seen where you are getting stuck.

Each buzz only costs you $10.99

I was wondering if there have been any neutrino bursts which have reached us a few years before the observance of a super nova? Surely we could've detected something like this by now. If not, are there any groups checking the data to see if we have observed this?

The algorithms could ensure that the money would be loaned out correctly, but we are still faced with the problems associated with greed. Also, if we give 100% control over to these computer systems, what would prevent an organization from developing methods that intentionally do harm to the global economy? Perhaps we need laws which prevent such activities and provide harsh penalties instead of relying on computers to help clean up and prevent our messes. Even though this is wishful thinking and there are a tremendous number of problems associated with such idea, I often ponder what would happen if we replaced our currency with handshakes. The economy could theoretically work no different than how it does with money. The only difference is that we use a handshake instead. This would cure a lot of the problems we face by coveting paper and gold. However, it is greed and our competitive nature which makes this solution impossible.

I wouldn't attribute the economic situation that most of the world is facing on algorithms that buy / sell stocks. The algorithms that these computers execute are based on a predetermined set of rules that are, none the less, created by us humans. As I understand the situation, the crisis is due to people living beyond their means by taking out loans they cannot repay, etc... Of course, I am no financial expert and there are probably many more factors that come into play. However, there may be some unforseen consequences that these computers are creating that may have or will impact the economy, as you seem to suggest. The stock market is more of a psychological entity where people buy and sell based on current trends and rumors instead of the actual state of particular businesses. These computers may misinterpret the input aquired and could disrupt the balance creating panic throughout global markets, but that is highly unlikely. I would speculate that these alogorithms are created with conservative trading methods in mind and are highly regulated.

Even though this is belated, congratulations Cap'n!!! I think it's really cool that you are into programming, numerical analysis, and physics. Those subjects along with finite calculus are some of my favorite areas of study. Also, teaching can be very rewarding. Currently, I am a substitute teacher for the high school where I graduated back in '98. It helps me earn a little extra money while working on my physics degree. There's nothing like talking to a few kids about physics only to have acquired the attention of the entire class. Keep up the good work. I wish you continued success throughout your collegiate years and those to come!!!

I have developed software professionally for over 11 years. I program in C, C++, C#, and some Visual Basic. I have developed software for Windows and Unix / Linux. I believe your question is referring to static linked libaries vs. dynamic linked libraries. Static linked libraries are typically linked into the image of the executable and thus are internal to the application where dynamic linked libraries reside outside of the executable and can be loaded externally by other processes. There are pros and cons to using a static or dynamic linked library. I suggest you review the above links to get a better understanding of each type of library. Otherwise, as Xittenn has stated, an internal libary would be one that is proprietary to the application and developed by the individual or company that designed the software. This is usually decided upon because the functionality does not exist and the individual or company has a need to create such library and intends to reuse the code in other applications they develop. An external library would be one that provides the functionality needed and prevents the individual or company from reinventing the wheel. External libraries in this case are referred to as third party libraries and components. The decision to use external libraries, APIs or SDKs, made by third parties can reduce development time and save companies a tremendous amount of money by not taking on the burden of design, implementation, and quality assurance that goes into developing a piece of software. However, great care must be asserted when dealing with third party libraries. A developer must be aware of the third party's responsibility of maintaining their code, fixing software issues, and costs of licensing. A company may choose to create their own libraries to avoid licensing fees or because they want to ensure the quality of their software.

That's a good one Phi for All : )

Since no one has provided me with the answer, I will go ahead and post the solution:

This one actually made me smile : )

I finally managed to get my blog setup and thought that my experience might help others who wish to do the same. Now I am not going to go into details on setting your site title and tagline. You can find those things very easily in your dashboard under settings->general. The purpose of this post is to explain how you can use CSS code to customize a Fusion 3.1 theme. First, you need to go to your dashboard and click "appearance->themes". Then, you will need to browse for the theme titled Fusion 3.1 by digitalnature. Once you have found the theme, you will want to click the "activate" link to set it as your blog theme. Now that you have Fusion 3.1 activated, you need to click "appearance->fusion settings". This option is only available for the Fusion theme. When the Fusion theme setting page loads, scroll to the very bottom. You should see a section titled "User CSS code". This allows you to override the appearance of your blog by inserting your own custom CSS code into this section. It is important to note that you are only overriding existing styles that are part of the theme. The reason I wanted to do this is because even though I liked the theme, there were a few things I didn't like about it. The tagline was displayed above the title and was obscurred by the menu at the top. I also didn't like the widget panel overlapping the header. So I decided to change these things. I searched the internet for the appropriate CSS code that would override those styles and managed to accomplish exactly what I wanted. I moved the tagline and resized the text so that it rendered under my site title. I also moved the widget panel down so that it was flush with the bottom of the header. I then removed the shadow around the widget panel so that it would blend nicely with the background. The following code snipet will allow you to have the same look: /* Reposition the tag line text and increase its size */ #topnav, #topnav a { font-size: 130%; padding-top: 140px; } /* Reposition the sidebar and remove the shadow */ #sidebar-wrap1 { background:none; margin-top: 200px; } #sidebar-wrap2 { background:none; } The next thing I wanted to do was use LaTeX in my blog. I searched our forums and couldn't find anything about using LaTeX in a blog post. So, I decided to give Google a try. It didn't take long to discover that instead of using the [ math ]...[ /math ] tags, you need to begin your LaTeX code with $latex and end with $. The following is an example of displaying a fraction in a blog post: $latex \frac{a}{b}$ which renders as: [math]\frac{a}{b}[/math] That's it for now on customizing the Fusion 3.1 theme. You can check out my blog by clicking the following link: http://blogs.science...s.net/Daedalus/ I hope this was helpful for those who want to customize their blog and use LaTeX in their posts : )

Hi rktpro, BoDs are normally hardware / driver errors. Check your event logs to see if any problems are reported. If you see some issues and can't figure out what it means, then post them here so we can help you.

That is awesome. Couple that with organs made to order, and we should see a new era in medicine like no other.

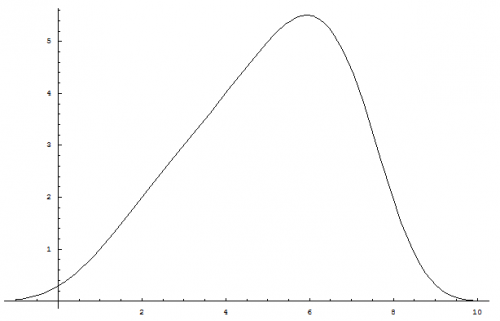
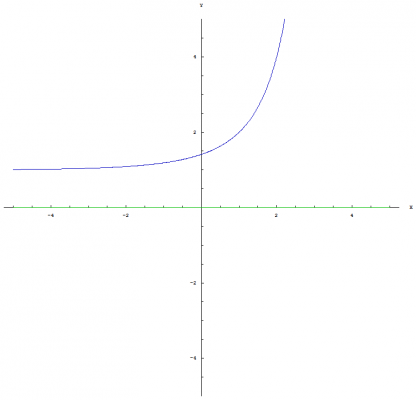
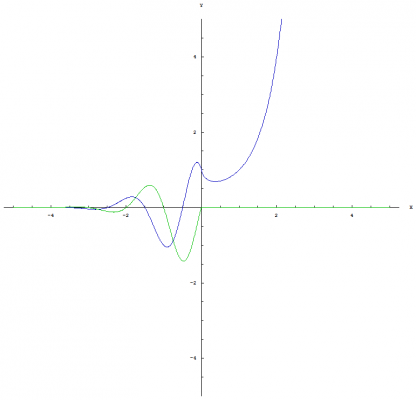
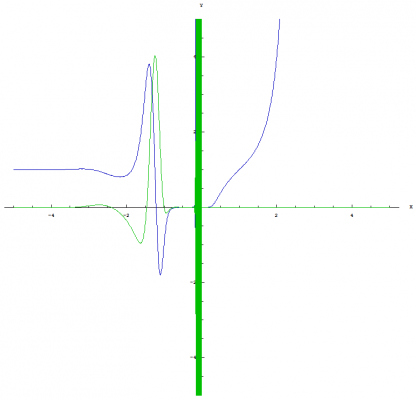
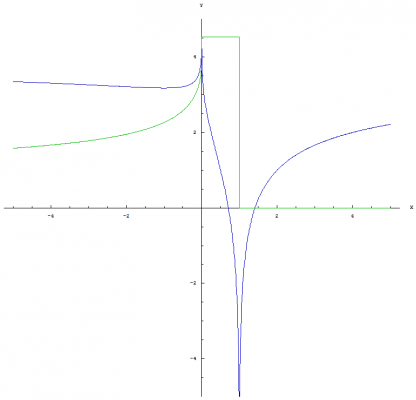
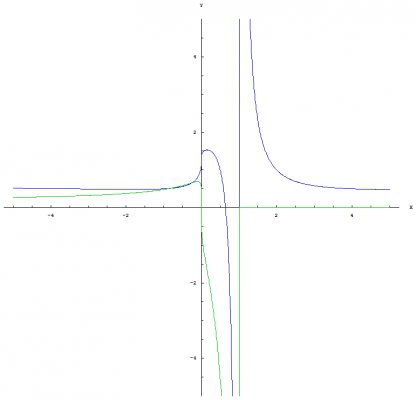
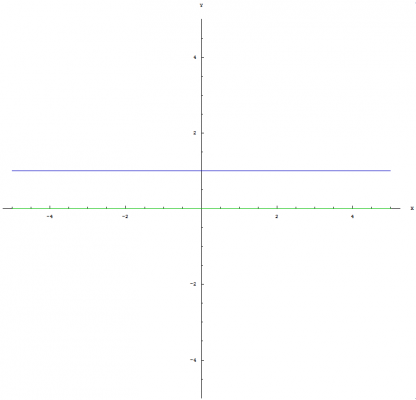
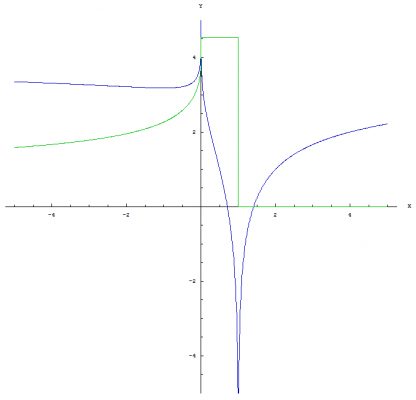
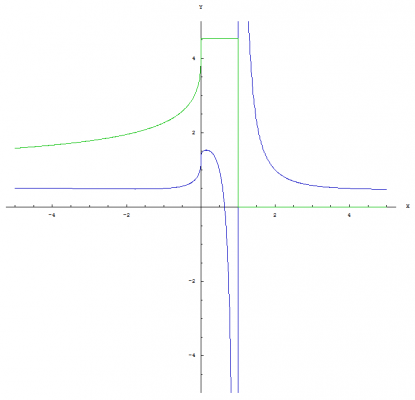
Yeah, that is why I asked if anyone had some thoughts on how nested exponentiation / nested logarithms could be written which would distinguish the operations from others that are similiar in nature. I like the notation that I developed. I just don't want it to be confusing. A few more trivial identities: [math]\left(a^{\left \langle b \right \rangle}\right)^{a^c}=\left(a^{a^{b-1}}\right)^{a^c}=a^{a^{b-1} a^{c}}=a^{a^{b+c-1}}=a^{\left \langle b+c \right \rangle}[/math] [math]\left(a^{\left \langle b \right \rangle}\right)^{a^{-c}}=\left(a^{a^{b-1}}\right)^{a^{-c}}=a^{a^{b-1} a^{-c}}=a^{a^{b-c-1}}=a^{\left \langle b-c \right \rangle}[/math] Graph of [math]x^{\left \langle a \right \rangle}[/math]: This graph shows both the real part (blue) and the imaginary part (green). Graph of [math]a^{\left \langle x \right \rangle}[/math]: This graph shows both the real part (blue) and the imaginary part (green). Graph of [math]x^{\left \langle x \right \rangle}[/math]: This graph shows both the real part (blue) and the imaginary part (green). Graph of [math]\text{nLog}_{\, a} \left(x\right)[/math]: This graph shows both the real part (blue) and the imaginary part (green). Graph of [math]\text{nLog}_{\, x} \left(a\right)[/math]: This graph shows both the real part (blue) and the imaginary part (green). Graph of [math]\text{nLog}_{\, x} \left(x\right)[/math]: This graph shows both the real part (blue) and the imaginary part (green).

If your formula controller has the floor or ceiling function you can play around with: Floor: [math]\lfloor \text{sin}(x) \rfloor[/math] Ceiling: [math]\lceil \text{sin}(x) \rceil[/math] You will probably have to play around with the amplitude due to the way those functions trim decimals, but it might suit your purposes.

Notation I've been thinking about the notation for nested exponentiation / nested logarithms and was wondering if anyone had some thoughts on how they could be written which would distinguish the operations from others that are similiar in nature. I used the following notation in the original post: Nested exponentiation: [math]a^{\left \langle b \right \rangle}[/math] [math]e^{\left \langle x \right \rangle}={}_n\, \!\text{Exp}\left(x\right)[/math] Nested logs: [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)[/math] Natural nested logs: [math]{}_n\, \!\text{Log}_{\, e}\left(b\right)={}_n\, \!\text{Ln}\left(b\right)[/math] But, this notation might be better because it doesn't imply that the [math]n[/math] is some sort of variable and requires less LaTeX syntax to display it: Nested Exponentiation: [math]e^{\left \langle x \right \rangle}=\text{nExp}\left(x\right)[/math] Nested logs: [math]\text{nLog}_{\, a}\left(b\right)[/math] Natural nested logs: [math]\text{nLog}_{\, e}\left(b\right)=\text{nLn}\left(b\right)[/math] The [math]n[/math] is being used to let us know that we are dealing with "nested" exonents and the capitalized [math]\text{L}[/math] and [math]\text{E}[/math] are meant to suggest that we are dealing with operations bigger than normal exponents. Both symbols are meant to distinguish these operators from the traditional logarithm and natural logarithm operations. I suppose both options would be acceptable. I am open to suggestions. Identities of Nested Exponentiation and Nested Logarithms I have derived some new properties of nested exponentiation and nested logarithms. I have listed these properties along with some trivial identities below. Trivial Identities: [math]a^{\left \langle 0 \right \rangle}=a^{a^{(0-1)}}=a^{a^{-1}}=a^{\frac{1}{a}}=\sqrt[a]{a}[/math] [math]a^{\left \langle 1 \right \rangle}=a^{a^{(1-1)}}=a^{a^0}=a[/math] [math]a^{\left \langle 2 \right \rangle}=a^{a^{(2-1)}}=a^{a^1}=a^a[/math] [math]\text{nLog}_{\, a}\left(a\right)=1+\frac{\text{ln}\left(\frac{\text{ln}\left(a\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}=1+\frac{\text{ln}\left(1\right)}{\text{ln}\left(a\right)}=1+\frac{0}{\text{ln}\left(a\right)}=1[/math] Both [math]\text{nLog}_{\, a}\left(0\right)[/math] and [math]\text{nLog}_{\, a}\left(1\right)[/math] are undefined: [math]\lim_{b \to 0}\big(\text{nLog}_{\, a}\left(b\right)\big) =\lim_{b \to 0} \left(1+\frac{\text{ln}\left(\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}\right)=\infty[/math] [math]\lim_{b \to 1}\big(\text{nLog}_{\, a}\left(b\right)\big) =\lim_{b \to 1} \left(1+\frac{\text{ln}\left(\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}\right)=-\infty[/math] Relationship to normal exponentials: [math]a^b=a\ \frac{\text{ln}\left(a^{\left \langle b \right \rangle}\right)}{\text{ln}\left(a\right)}=a\ \text{log}_{\, a}\left(a^{\left \langle b \right \rangle}\right)[/math] Proof: Nested exponentiation by definition: [math]a^{\left \langle b \right \rangle}=a^{a^{(b-1)}}[/math] Take the natural log of both sides: [math]\text{ln}\left(a^{a^{(b-1)}}\right)=\text{ln}\left(a^{\left \langle b \right \rangle}\right)[/math] Simplify the result: [math]a^{(b-1)}\, \text{ln}\left(a\right)=\text{ln}\left(a^{\left \langle b \right \rangle}\right)[/math] Divide both sides by [math]\text{ln}\left(a\right)[/math]: [math]a^{(b-1)}=\frac{\text{ln}\left(a^{\left \langle b \right \rangle}\right)}{\text{ln}\left(a\right)}[/math] Multiply both sides by [math]a[/math]: [math]a^{b}=a\ \frac{\text{ln}\left(a^{\left \langle b \right \rangle}\right)}{\text{ln}\left(a\right)}[/math] Convert [math]\text{ln}\left(a^{\left \langle b \right \rangle}\right) / \text{ln}\left(a\right)[/math] to a logarithm by the "changing the base" identity: [math]a^{b}=a\ \text{log}_{\, a}\left(a^{\left \langle b \right \rangle}\right)[/math] Q.E.D. Relationship between nested logarithms and natural nested logarithms: [math]\text{nLog}_{\, a}\left(b\right) = 1+\frac{\text{nLn}\left(b\right) - \text{nLn}\left(a\right)}{\text{ln}\left(a\right)}[/math] Proof: Natural nested logarithm by definition from the previous post: [math]\text{nLn}\left(x\right)=1+\text{ln}\left(\text{ln}\left(x\right)\right)[/math] Nested logarithm by definition from the previous post: [math]\text{nLog}_{\, a}\left(b\right) =1+\frac{\text{ln}\left(\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}= 1+\frac{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}{\text{ln}\left(a\right)}[/math] Such that: [math]1+\frac{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}{\text{ln}\left(a\right)}=1+\frac{\left(1+\text{ln}\left(\text{ln}\left(b\right)\right)\right)-\left(1+\text{ln}\left(\text{ln}\left(a\right)\right)\right)}{\text{ln}\left(a\right)}[/math] Simplify the right side by cancelling the ones in the numerator: [math]1+\frac{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}{\text{ln}\left(a\right)}=1+\frac{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}{\text{ln}\left(a\right)}[/math] Q.E.D. This bring us to another interesting relationship: [math]\text{nLn}\left(b\right) - \text{nLn}\left(a\right)=\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)[/math] Such that: [math]e^{\text{nLn}\left(b\right) - \text{nLn}\left(a\right)}=e^{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}=\text{log}_{\, a}\left(b\right)[/math] Proof: [math]1+\frac{\text{nLn}\left(b\right) - \text{nLn}\left(a\right)}{\text{ln}\left(a\right)}=1+\frac{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}{\text{ln}\left(a\right)}[/math] Subtract one from both sides: [math]\frac{\text{nLn}\left(b\right) - \text{nLn}\left(a\right)}{\text{ln}\left(a\right)}=\frac{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}{\text{ln}\left(a\right)}[/math] Multiply both sides by [math]\text{ln}\left(a\right)[/math]: [math]\text{nLn}\left(b\right) - \text{nLn}\left(a\right)=\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)[/math] Raise [math]e[/math] to the power of both sides: [math]e^{\text{nLn}\left(b\right) - \text{nLn}\left(a\right)}=e^{\text{ln}\left(\text{ln}\left(b\right)\right)-\text{ln}\left(\text{ln}\left(a\right)\right)}[/math] Undo the subtraction in the exponent: [math]\frac{e^{\text{nLn}\left(b\right)}}{e^{\text{nLn}\left(a\right)}}=\frac{e^{\text{ln}\left(\text{ln}\left(b\right)\right)}}{e^{\text{ln}\left(\text{ln}\left(a\right)\right)}}[/math] Simplify the result: [math]\frac{e^{1+\text{ln}\left(\text{ln}\left(b\right)\right)}}{e^{1+\text{ln}\left(\text{ln}\left(a\right)\right)}}=\frac{e\ \text{ln}\left(b\right)}{e\ \text{ln}\left(a\right)}=\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}[/math] Cancel out the [math]e[/math] and change the base: [math]e^{\text{nLn}\left(b\right) - \text{nLn}\left(a\right)}=\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}=\text{log}_{\, a}\left(b\right)[/math] Q.E.D. The nested logarithm of a double nested exponential with the same base (or something like that lol): [math]\text{nLog}_{\, a}\left(\left(a^{\left \langle b \right \rangle}\right)^{\left \langle c \right \rangle}\right)=\left(c-1\right)\, a^{(b-1)}+b[/math] Proof: [math]\left(a^{\left \langle b \right \rangle}\right)^{\left \langle c \right \rangle}=\left(a^{\left \langle b \right \rangle}\right)^{\left(a^{\left \langle b \right \rangle}\right)^{(c-1)}}=\left(a^{a^{(b-1)}}\right)^{\left(a^{a^{(b-1)}}\right)^{(c-1)}}=[/math] [math]\left(a^{a^{(b-1)}}\right)^{\left(a^{(c-1)\, a^{(b-1)}}\right)}=a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}[/math] Take the natural log of the simplified version: [math]\text{ln}\left(a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}\right)=\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right) \text{ln}\left(a\right)[/math] Divide both sides by [math]\text{ln}\left(a\right)[/math]: [math]\frac{\text{ln}\left(a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}\right)}{\text{ln}\left(a\right)}=\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)[/math] Take the natural log of both sides: [math]\text{ln}\left(\frac{\text{ln}\left(a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}\right)}{\text{ln}\left(a\right)}\right)=\text{ln}\left(\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)\right)[/math] Simplify the right hand side: [math]\text{ln}\left(\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)\right)=\text{ln}\left(a^{(b-1)}\right) + \text{ln}\left(a^{(c-1)\, a^{(b-1)}}\right)=[/math] [math](b-1) \, \text{ln}\left(a\right)\, + \, (c-1)\, a^{(b-1)} \, \text{ln}\left(a\right)=\text{ln}\left(a\right)\, \left((b-1)\, +\, (c-1)\, a^{(b-1)}\right)[/math] Such that: [math]\text{ln}\left(\frac{\text{ln}\left(a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}\right)}{\text{ln}\left(a\right)}\right)=\text{ln}\left(a\right)\, \left((b-1)\, +\, (c-1)\, a^{(b-1)}\right)[/math] Divide both sides by [math]\text{ln}\left(a\right)[/math]: [math]\frac{\text{ln}\left(\frac{\text{ln}\left(a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}=(b-1) \, + \, (c-1)\, a^{(b-1)}[/math] Complete the nested logarithm by adding one to both sides: [math]1+\frac{\text{ln}\left(\frac{\text{ln}\left(a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}=1+(b-1) \, + \, (c-1)\, a^{(b-1)}[/math] Simplify the result: [math]\text{nLog}_{\, a}\left(\left(a^{\left \langle b \right \rangle}\right)^{\left \langle c \right \rangle}\right)=1+\frac{\text{ln}\left(\frac{\text{ln}\left(a^{\left(a^{(b-1)}\right)\left(a^{(c-1)\, a^{(b-1)}}\right)}\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}=(c-1)\, a^{(b-1)}\, +\, b[/math] Q.E.D. Graph of [math]\text{nLog}_{\, a}\left(x\right)[/math]: This graph shows both the real part (blue) and the imaginary part (green) Graph of [math]\text{nLog}_{\, x}\left(a\right)[/math]: This graph shows both the real part (blue) and the imaginary part (green) That's it for now. I hope you all enjoy reading this post : ) I just realized that on the graph of [math]\text{nLog}_{\, x}\left(a\right)[/math], located at the bottom, I did not plot the correct equation for the imaginary part. I will post the correct graph when I get home tomorrow. (bugfix?)

The Next Operator Beyond Exponents: I was looking into operations greater than exponents when I discovered a few properties of nested exponentiation. I'm not claiming that I am the first to discover these properties. I am well aware of work that has been done on tetration and the Ackermann function. However, I have not found these properties of nested exponentiation anywhere. Also, according to Wikipedia, nested exponentation is not even listed as a hyperoperation: Another clue is that my version of Mathematica does not have any of these properties listed as operators and does not know how to simplify equations using the new operations I have derived. I fully understand that this does not mean that I am truly the first one to discover these properties, but I have been searching for a reference to them ever since I discovered these properties in 2005. Also, I have shown these to a few math professors at UCO and OU. They were completely unaware of these operations themselves and told me to do further research in the math library, which I have done. If you are aware of these properties, then please provide a link so that I can read up on who discovered them and how they are applied. Nested Exponentiation: Most of us are aware of nested exponents and how to simplify the math that uses them: [math](a^b)^c=a^{b\, c}[/math] So I began to wonder about series of nested exponents and if I could derive any properties associated with them. Now I do realize that this next part may be known, but here is the relationship for a series of nested exponents along with how I denote nested exponentiation: [math]a^{\left \langle n \right \rangle} = \underbrace{(((a)^a)^a)^{\cdot^{\cdot^{a}}}}_n = a^{a^{n-1}}[/math] We can demonstrate this by the following: [math]a^{\left \langle 1 \right \rangle} = a = a^{a^{(1-1)}}[/math] [math]a^{\left \langle 2 \right \rangle} = (a)^a = a^{a^{(2-1)}}[/math] [math]a^{\left \langle 3 \right \rangle} = ((a)^a)^a = a^{a^{(3-1)}}[/math] [math]a^{\left \langle 4 \right \rangle} = (((a)^a)^a)^a = a^{a^{(4-1)}}[/math] Now that we have the generalized form, [math]a^{a^{n-1}}[/math], that predicts the outcome of continued nested exponentiation, we can derive the derivatives / integrals using Calculus and define an algorithm for determining nested roots using the Newton-Rhapson method. However, the operation that I believe is new is what I call the nested logarithm. The nested log is just like normal logarithms except it determines the value of the nested exponent: [math]{}_n\, \!\text{Log}_{\, a}\left(a^{\left \langle b \right \rangle}\right)=b[/math] I've also managed to work out a few generalized forms of the nested logarithm: [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1+\frac{\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}[/math] [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1-\frac{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)}{\text{ln}\left(a\right)}[/math] Proof that [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1+\text{ln}(\text{ln}(b) / \text{ln}(a)) / \text{ln}(a)[/math] : Let [math]a[/math] equal the base of the nested exponent and let [math]b[/math] equal [math]a^{\left \langle n \right \rangle}[/math] which is also equal to [math]a^{a^{n-1}}[/math] : [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)={}_n\, \!\text{Log}_{\, a}\left(a^{\left \langle n \right \rangle}\right)={}_n\, \!\text{Log}_{\, a}\left(a^{a^{n-1}}\right)=n[/math] We can now use the general form, [math]a^{a^{n-1}}[/math], to derive the nested logarithm by using natural logarithms: [math]\text{ln}\left(a^{a^{n-1}}\right)=a^{n-1} \, \text{ln}\left(a\right)[/math] Divide both sides by [math]\text{ln}\left(a\right)[/math]: [math]\frac{\text{ln}\left(a^{a^{n-1}}\right)}{\text{ln}\left(a\right)}=a^{n-1}[/math] Take the natural log of both sides: [math]\text{ln}\left(\frac{\text{ln}\left(a^{a^{n-1}}\right)}{\text{ln}\left(a\right)}\right)=\left(n-1\right) \, \text{ln}\left(a\right)[/math] Again, divide both sides by [math]\text{ln}\left(a\right)[/math]: [math]\frac{\text{ln}\left(\frac{\text{ln}\left(a^{a^{n-1}}\right)}{\text{ln}\left(a\right)}\right)}{ \text{ln}\left(a\right)}=n-1[/math] Add one to both sides: [math]1+\frac{\text{ln}\left(\frac{\text{ln}\left(a^{a^{n-1}}\right)}{\text{ln}\left(a\right)}\right)}{ \text{ln}\left(a\right)}=n[/math] Substitute [math]a^{\left \langle n \right \rangle}[/math] in place of [math]a^{a^{n-1}}[/math]: [math]{}_n\, \!\text{Log}_{\, a}\left(a^{\left \langle n \right \rangle}\right)=1+\frac{\text{ln}\left(\frac{\text{ln}\left(a^{\left \langle n \right \rangle}\right)}{\text{ln}\left(a\right)}\right)}{ \text{ln}\left(a\right)}=n[/math] Substitute [math]b[/math] in place of [math]a^{\left \langle n \right \rangle}[/math]: [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1+\frac{\text{ln}\left(\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)}{ \text{ln}\left(a\right)}[/math] Q.E.D. Proof that [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1-\text{ln}(\text{ln}(a) / \text{ln}(b)) / \text{ln}(a)[/math] : Working backwards, we can prove that the second form is true. Let [math]a[/math] equal the base of the nested exponent and let [math]b[/math] equal [math]a^{\left \langle n \right \rangle}[/math] which is also equal to [math]a^{a^{n-1}}[/math] such that: [math]1-\frac{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(a^{\left \langle n \right \rangle}\right)}\right)}{\text{ln}\left(a\right)}=1-\frac{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(a^{a^{n-1}}\right)}\right)}{\text{ln}\left(a\right)}=n[/math] Swap the variable [math]n[/math] and the term using the natural logarithms: [math]1-n=\frac{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(a^{a^{n-1}}\right)}\right)}{\text{ln}\left(a\right)}[/math] Multiply both sides by [math]\text{ln}\left(a\right)[/math]: [math](1-n)\, \text{ln}\left(a\right)=\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(a^{a^{n-1}}\right)}\right)[/math] Raise [math]e[/math] to the power of each side: [math]e^{(1-n)\, \text{ln}\left(a\right)}=e^{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(a^{a^{n-1}}\right)}\right)}[/math] Simplify the result: [math]a^{1-n}=\frac{\text{ln}\left(a\right)}{\text{ln}\left(a^{a^{n-1}}\right)}[/math] Multiply both sides by [math]\text{ln}\left(a^{a^{n-1}}\right)[/math]: [math]a^{1-n}\, \text{ln}\left(a^{a^{n-1}}\right)=\text{ln}\left(a\right)[/math] Divide both sides by [math]a^{1-n}[/math]: [math]\text{ln}\left(a^{a^{n-1}}\right)=\frac{\text{ln}\left(a\right)}{a^{1-n}}[/math] Raise [math]e[/math] to the power of each side: [math]e^{\text{ln}\left(a^{a^{n-1}}\right)}=e^{\frac{\text{ln}\left(a\right)}{a^{1-n}}}[/math] Simplify the result: [math]a^{a^{n-1}}=a^{a^{n-1}}[/math] Q.E.D. Properties of nested exponentiation: [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1+\frac{\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)} \ \ \ \ \ \ \ {}_n\, \!\text{Log}_{\, a}\left(b\right)=1-\frac{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)}{\text{ln}\left(a\right)}[/math] [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1+\text{log}_{a}\left(\text{log}_{a}\left(b\right)\right) \ \ \ \ \ \ \ {}_n\, \!\text{Log}_{\, e}\left(b\right)=1+\text{ln}\left(\text{ln}\left(b\right)\right)[/math] [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)=1-\frac{\text{ln}\left(\text{ln}\left(a\right)\right)}{\text{ln}\left(a\right)}+\frac{\text{ln}\left(\text{ln}\left(b\right)\right)}{\text{ln}\left(a\right)} \ \ \ \ \ \ \ \text{log}_{\, a}\left(b\right)=\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}=a^{\left({}_n\, \!\text{Log}_{\, a}\left(b\right)-1\right)}[/math] [math]\text{ln}\left(\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)=\text{ln}\left(a\right) \left({}_n\, \!\text{Log}_{\, a}\left(b\right) - 1\right) \ \ \ \ \ \ \ \text{ln}\left(\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)=\text{ln}\left(a\right) \left(1-{}_n\, \!\text{Log}_{\, a}\left(b\right)\right)[/math] Mathematica 5.2 cannot determine that this identity equals zero: [math]\left(1+\frac{\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)}\right)-\left(1-\frac{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)}{\text{ln}\left(a\right)}\right)=0[/math] It produces the following: [math]\frac{\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right) + \text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)}{\text{ln}\left(a\right)}[/math] Every number I plug in produces zero, which is what is expected as determined by the above proofs. The following identity is true as determined by the proof below: [math]\frac{\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right) + \text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)}{\text{ln}\left(a\right)} = 0[/math] [math]\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right) + \text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right) = 0[/math] Proof: Raise [math]e[/math] to the above identity: [math]e^{\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right) + \text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)}=1[/math] This is equal to: [math]e^{\text{ln}\left (\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)}\right)} \times e^{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)}\right)}=1[/math] Which simplifies to: [math]\frac{\text{ln}\left(b\right)}{\text{ln}\left(a\right)} \times \frac{\text{ln}\left(a\right)}{\text{ln}\left(b\right)} = 1[/math] Q.E.D. Derivatives for nested exponents (Found by using Mathematica): [math]\frac{dy}{dx} \ x^{\left \langle a \right \rangle} = x^{x^{(a-1)}}\left(x^{(a-2)}\left(1+\left(a-1\right)\, \text{ln}\left(x\right)\right)\right)=x^{\left \langle a \right \rangle}\left(x^{(a-2)}\left(1+\left(a-1\right)\, \text{ln}\left(x\right)\right)\right)[/math] [math]\frac{dy}{dx} \ a^{\left \langle x \right \rangle} = a^{a^{(x-1)}} \, a^{(x-1)} \, \text{ln}\left(a\right)^2=a^{\left \langle x \right \rangle} \left(a^{(x-1)} \, \text{ln}\left(a\right)^2\right)[/math] [math]\frac{dy}{dx} \ x^{\left \langle x \right \rangle} = x^{x^{(x-1)}}\left(x^{(x-2)}+x^{(x-1)}\, \text{ln}\left(x\right)\left(\text{ln}\left(x\right)+\frac{x-1}{x}\right)\right)=x^{\left \langle x \right \rangle}\left(x^{(x-2)}+x^{(x-1)}\, \text{ln}\left(x\right)\left(\text{ln}\left(x\right)+\frac{x-1}{x}\right)\right)[/math] [math]\frac{dy}{dx} \ {}_n\, \!\text{Log}_{\, a}\left(x\right) = \frac{1}{x\, \text{ln}\left(x\right)\, \text{ln}\left(a\right)}=\frac{{}_n\, \!\text{Log}_{\, a}\left(x\right)}{x\, \text{ln}\left(x\right) \left(\text{ln}\left(a\right) +\text{ln}\left(\frac{\text{ln}\left(x\right)}{\text{ln}\left(a\right)}\right)\right)}[/math] [math]\frac{dy}{dx} \ {}_n\, \!\text{Log}_{\, x}\left(a\right) = \frac{\text{ln}\left(\frac{\text{ln}\left(x\right)}{\text{ln}\left(a\right)}\right)-1}{x\, \text{ln}\left(x\right)^2}=\frac{\text{ln}\left(x\right) \left(1-{}_n\, \!\text{Log}_{\, x}\left(a\right)\right)-1}{x\, \text{ln}\left(x\right)^2}[/math] Properties of Derivatives for nested exponents (Found by using Mathematica): Nested exponential function that has the constant as the nested exponent, [math]x^{\left \langle a \right \rangle}[/math]: [math]\frac{dy}{dx} \ \text{ln}\left(x^{\left \langle a \right \rangle}\right) = \left(x^{(a-2)}\left(1+\left(a-1\right)\, \text{ln}\left(x\right)\right)\right)[/math] Which allows us to define the following by substitution: [math]\frac{dy}{dx} \ x^{\left \langle a \right \rangle} = x^{\left \langle a \right \rangle} \ \frac{dy}{dx} \ \text{ln}\left(x^{\left \langle a \right \rangle}\right)[/math] Such that: [math]x^{\left \langle a \right \rangle}=\frac{\frac{dy}{dx} \ x^{\left \langle a \right \rangle}}{\frac{dy}{dx} \ \text{ln}\left(x^{\left \langle a \right \rangle}\right)}[/math] Nested exponential function that has the variable as the nested exponent, [math]a^{\left \langle x \right \rangle}[/math]: [math]\frac{dy}{dx} \ \text{ln}\left(a^{\left \langle x \right \rangle}\right) = \left(a^{(x-1)} \, \text{ln}\left(a\right)^2\right)[/math] Which allows us to define the following by substitution: [math]\frac{dy}{dx} \ a^{\left \langle x \right \rangle} = a^{\left \langle x \right \rangle} \ \frac{dy}{dx} \ \text{ln}\left(a^{\left \langle x \right \rangle}\right)[/math] Such that: [math]a^{\left \langle x \right \rangle}=\frac{\frac{dy}{dx} \ a^{\left \langle x \right \rangle}}{\frac{dy}{dx} \ \text{ln}\left(a^{\left \langle x \right \rangle}\right)}[/math] Nested exponential function that has the variable as the base and as the nested exponent, [math]x^{\left \langle x \right \rangle}[/math]: [math]\frac{dy}{dx} \ \text{ln}\left(x^{\left \langle x \right \rangle}\right) = \left(x^{(x-2)}+x^{(x-1)}\, \text{ln}\left(x\right)\left(\text{ln}\left(x\right)+\frac{x-1}{x}\right)\right)[/math] Which allows us to define the following by substitution: [math]\frac{dy}{dx} \ x^{\left \langle x \right \rangle} = x^{\left \langle x \right \rangle} \ \frac{dy}{dx} \ \text{ln}\left(x^{\left \langle x \right \rangle}\right)[/math] Such that: [math]x^{\left \langle x \right \rangle}=\frac{\frac{dy}{dx} \ x^{\left \langle x \right \rangle}}{\frac{dy}{dx} \ \text{ln}\left(x^{\left \langle x \right \rangle}\right)}[/math] Integrals for nested exponents (Found by using Mathematica): There are no general expressions for the integrals. They are based on the exponential integral, logarithmic integral, or unknown. Here is what Mathematica derived: [math]\int x^{\left \langle a \right \rangle} \, dx = \int x^{x^{a-1}} \, dx = \text{unknown}[/math] [math]\int a^{\left \langle x \right \rangle} \, dx = \int a^{a^{x-1}} \, dx = \frac{\text{Ei}\left(a^{x-1}\, \text{ln}(a)\right)}{\text{ln}(a)}+C[/math] [math]\int x^{\left \langle x \right \rangle} \, dx = \int x^{x^{x-1}} \, dx = \text{unknown}[/math] [math]\int {}_n\, \!\text{Log}_{\, a}\left(x\right) \, dx = \int 1\, +\, \frac{\text{ln}\left (\frac{\text{ln}\left(x\right)}{\text{ln}\left(a\right)}\right)}{\text{ln}\left(a\right)} \, dx = x \, + \, \frac{x \, \text{ln}\left(\frac{\text{ln}(x)}{\text{ln}(a)}\right)}{\text{ln}(a)}\, -\, \frac{\text{li}(x)}{\text{ln}(a)}\, +\, C = x\, \left({}_n\, \!\text{Log}_{\, a}\left(x\right)\right)\, -\, \frac{\text{li}(x)}{\text{ln}(a)}\, +\, C[/math] [math]\int {}_n\, \!\text{Log}_{\, x}\left(a\right) \, dx = \int 1+\frac{\text{ln}\left (\frac{\text{ln}\left(a\right)}{\text{ln}\left(x\right)}\right)}{\text{ln}\left(x\right)} \, dx = \text{unknown}[/math] The exponential integral, [math]\text{Ei}(x)[/math]: [math]\text{Ei}(x)=\int \limits_{-\infty}^{x} \frac{e^t}{t} \, dt[/math] The logarithmic integral, [math]\text{li}(x)[/math]: [math]\text{li}(x)=\int \limits_{0}^{x} \frac{dt}{\text{ln}(t)}[/math] Finding nested roots and nested logarithms using the Newton-Rhapson method: First it is important to note that the Newton-Rhapson method may fail to converge to the desired result. One must read and understand the proof of quadratic convergence for Newton's iterative method which is described in Wikipedia. With that being said I have not had a problem finding nested roots or nested logarithms using this approach. [math]x_{n+1}=x_{n} - \frac{f(x_{n})}{f'(x_{n})}[/math] Nested Roots: To find the nested root we must use the nested exponential function that has the constant as the nested exponent, [math]x^{\left \langle a \right \rangle}[/math]. Using this function with Newton's method yields the following algorithm for nested roots (Repeat the process until you have obtained the desired result): [math]\sqrt[\left \langle a \right \rangle]{b}\ \ \ \ \text{approximated by} \ \ \ \ x_{n+1}=x_{n} - \frac{\left(x_{n}\right)^{\left(x_{n}\right)^{(a-1)}}-b}{\left(x_{n}\right)^{\left(x_{n}\right)^{(a-1)}}\left(\left(x_{n}\right)^{(a-2)}\left(1+\left(a-1\right)\, \text{ln}\left(x\right)\right)\right)}[/math] Nested Logarithms: To find the nested logarithm we must use the nested exponential function that has the variable as thenested exponent, [math]a^{\left \langle x \right \rangle}[/math]. Using this function with Newton's method yields the following algorithm for nested logarithms (Repeat the process until you have obtained the desired result): [math]{}_n\, \!\text{Log}_{\, a}\left(b\right)\ \ \ \text{approximated by} \ \ \ x_{n+1}=x_{n} - \frac{a^{a^{\left(x_{n}\right)-1}}-b}{a^{a^{\left(x_{n}\right)-1}} a^{\left(x_{n}\right)-1} \text{ln}\left(a\right)^2}[/math] I'm sorry about all of the edits. I was making sure that I had all of the properties that I have derived posted and I had to correct a few things. This sums it up for now. I will continue to post to this thread whenever I find something new. Also, I have a lot of mathematics which might be new that I will be posting here. I hope you all have enjoyed reading this thread : ) If anyone can suggest a few good places to publish my work, I'd be most appreciative. Otherwise, I will consult with one of my professors this Thursday unless someone can show me that this work has already been done. (bugfix)