Daedalus

I'm talking about the motion inside the atom itself in referring to your statement about oscillating energy levels. I understand that they don't physically move the clock and that they cool it off to near absolute zero. The fact that absolute zero cannot be obtained shows that motion in the atom still exists and it is this motion that they use to measure time in modern atomic clocks. I am aware that if an Einstein-Rosen Bridge, or wormhole, connected two temporally displaced views of the universe, then the mass-energy from both views, or "temporally parallel universes", might be able to directly interact due to these intersection points.

Any form of oscillation whether it's in energy levels or purely mechanical is still motion nonetheless. Something has to be in motion in order to induce a change in the energy levels. Nice comment though. It's time for me to go to bed, I look forward to reading what others think about this idea. I'm really interested in a solid proof that can disprove this view of time. However, I'm not sure one can be provided. If you can challenge this view, then by all means let us know why.

Point well made. However, I should not have to hide the limits of my knowledge. I'd rather someone know that I have a limited knowledge of GR so that they can provide a proof that will help direct my way of thinking, rather than let them assume that I imply to understand GR only to have misinterpreted the theory from their point of view. One way to view time as motion through the fourth dimension would be as follows: We will begin at a position located at time zero at the center of the big bang. This frame of reference will remain at time zero at the center of the big bang, observing the expansion of the universe from this view. Let there be a light clock located at this frame of reference and let us synchronize this light clock in accordance to the definitions in special relativity. We shall denote the time it takes for light to travel from point A to point B and back to point A in this frame of reference as [math]\Delta t_{b}[/math]. The subscript [math]b[/math] denotes the big bang reference. According to SR the light clock in this frame of reference would measure time according to: [math]\Delta t_{b} = \frac{2L}{c}[/math] where [math]L=|AB|[/math] If time was nothing more than motion, then the observer in this reference frame would infer motion through time by observing the expansion of the big bang. So their light clock would still be able to bounce light between two reflective surfaces because, even though they are not moving with the expansion of the big bang, motion would still be possible. Now let us consider the motion of an identical light clock that is radiating outward from the big bang, through the fourth dimension, relative to the big bang frame of reference. We shall denote the time observed by this clock as [math]\Delta t_{w}[/math]. The subscript [math]w[/math] denotes the spatial axis of time. The use of [math]w[/math] to label the time axis is to avoid confusion with the time variable [math]t[/math]. This frame of reference is called the time-normal frame as it defines a frame of reference that is only moving through the fourth dimension, time, away from the big bang. This is normally called the lab frame of reference. It is important to note that in all frames of reference, an observer will see their light clock no differently than the observer at the big bang frame of reference. The equations of relativity predict how one observer will view the other and vice-versa. This means that the observer in the big bang frame of reference will not see the path of the light from the light clock in motion relative to their position as a straight up and down path. The same is true for the observer in motion as they will see the light from the light clock positioned at the big bang frame of reference the same way. The path that is observed is that of a triangle instead of one that is straight up and down. Because Einstein proved the constancy of the speed of light, the difference in time measured as observed from each frame of reference is: [math]\Delta t_{n} = \frac{2N}{c}[/math] where [math]N=\sqrt{(\frac{V_{w} \times \Delta t_{n}}{2})^{2}+L^{2}}[/math] [math]V_{w}[/math] is the velocity through the fourth dimension and [math]L=|AB|[/math] Finally, we shall place another identical light clock that is in relative motion with the clock in the time-normal frame of reference, except these two clocks share the same position, speed, and direction through the temporal dimension. Therefore, the only relative motion between them is through spatial dimensions that are perpendicular to their forward motion through time. This means that both clocks have a relative velocity of zero along the temporal dimension and a non-zero relative velocity along the [math]x, y[/math] and [math]z[/math] axis of space. We shall denote time in this frame of reference as [math]\Delta t_{r}[/math]. The subscript [math]r[/math] denotes the time-relative frame of reference. We shall derive the equation for time dilation for this frame of reference in respect to the big bang frame of reference. This allows us to derive the following relationship: [math]\Delta t_{r} = \frac{2R}{c}[/math] where [math]R=\sqrt{(\frac{V_{w} \times \Delta t_{r}}{2})^{2}+(\frac{V_{r} \times \Delta t_{r}}{2})^{2}+L^{2}}[/math] [math]V_{w}[/math] is the velocity through the fourth dimension, [math]V_{r}[/math] is the velocity through all other spatial dimensions, and [math]L=|AB|[/math] Now that we have derived the equations for both frames of reference that are moving away from the big bang, we can relate them back to the big bang frame of reference according to the following: Solving for [math]\Delta t_{n}[/math] in the time-normal frame of reference we get: [math]\Delta t_{n} = \frac{2L/c}{\sqrt{1-\frac{V_{w}^{2}}{c^{2}}}}=\frac{\Delta t_{b}}{\sqrt{1-\frac{V_{w}^{2}}{c^{2}}}}[/math] Solving for [math]\Delta t_{r}[/math] in the time-relative frame of reference we get: [math]\Delta t_{r} = \frac{2L/c}{\sqrt{1-\frac{V_{w}^{2}}{c^{2}}-\frac{V_{r}^{2}}{c^{2}}}}=\frac{\Delta t_{b}}{\sqrt{1-\frac{V_{w}^{2}}{c^{2}}-\frac{V_{r}^{2}}{c^{2}}}}[/math] We can see that from the above relationships that the time-normal frame of reference is related to the time-relative frame of reference as follows: [math]\Delta t_{r} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}-\frac{V_{r}^{2}}{c^{2}}}=\Delta t_{n} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}}[/math] This allows us to derive the following relationship between the time-normal frame of reference and the time-relative frame of reference: [math]\Delta t_{r} =\Delta t_{n} \frac{\sqrt{1-\frac{V_{w}^{2}}{c^{2}}}}{\sqrt{1-\frac{V_{w}^{2}}{c^{2}}-\frac{V_{r}^{2}}{c^{2}}}}=\frac{\Delta t_{n}}{\sqrt{1-\frac{V_{r}^{2}}{c^{2}-V_{w}^{2}}}} [/math] This result makes sense because everything has a relative temporal velocity of zero: [math]\Delta t_{r}=\frac{\Delta t_{n}}{\sqrt{1-\frac{V_{r}^{2}}{c^{2}-0^{2}}}}=\frac{\Delta t_{n}}{\sqrt{1-\frac{V_{r}^{2}}{c^{2}}}}[/math] But, [math]V_{w}[/math] becomes apparent from the big bang frame of reference such that: [math]V_{w}=\frac{\sqrt{c^{2}(\Delta t_{n}^{2}-\Delta t_{r}^{2})+\Delta t_{r}^{2}\times V_{r}^{2}}}{\sqrt{\Delta t_{n}^{2}-\Delta t_{r}^{2}}}=\sqrt{c^{2}+\frac{\Delta t_{r}^{2}\times V_{r}^{2}}{\Delta t_{n}^{2}-\Delta t_{r}^{2}}}[/math] Interpreting this result seems to reveal that we move at a velocity other than the speed of light through the dimension of time. This is due to the relative velocity [math]V_{r}[/math] through the other spatial dimensions. However, when we place ourselves in the big bang frame of reference, we realize that [math]V_{r}=0[/math]. This is because all observers will place themselves in the time-normal frame of reference with all other bodies being time-relative in respect to their position. Therefore, all observers have zero relative velocity. [math]V_{w}=\sqrt{c^{2}+\frac{\Delta t_{r}^{2}\times 0^{2}}{\Delta t_{n}^{2}-\Delta t_{r}^{2}}}=\sqrt{c^{2}}=c[/math] So if we can deduce through mathematics that time is motion through the fourth dimension at the speed of light, shouldn't my notions about time travel be true in regards to the impossibility of traveling to a time that exists as a memory of the past or will exist as a memory in the future?

I never said that my view went against GR. I made a statement that I do not have enough knowledge of GR to determine how this view of time works out with mass-energy being spread out temporally.

I am aware that these "parallel universes" would be nothing more than a different view of our universe. I was just making a statement that they would not have the same mass-energy located at our point moving through time. So they would appear to be completely unique universes with their own history unique from ours. However, if time is nothing but motion through a fourth dimension, then it would be possible to explain dark matter as temporally displaced matter with observable gravitational effects from our point in time. But this is where my knowledge ends because I do not have a complete understanding of GR and how it would treat this view of time. I would like to state the relativistic speed is not the same as time-travel. This is because you would theoretically be observable along each and every point of your trajectory. You do not disapear and reappear in the future or past. This suggests that instead of traveling faster or slower through time, that the rate at which your atomic processes oscillate govern your aging process and affects your motions as you approach the speed of light. If we observe particles on the surface of Earth that should have decayed, it may be a function of the particles oscillation and not one of time.

When we make a measurement of a physical phenomena, we can only do so by taking advantage of an attribute inherent in the phenomena itself. For instance, we use a rod to measure length. The rod has markings that allow us to measure lengths that are within its boundaries. We use a voltmeter to measure electrical potential differences between two points. The voltmeter uses attributes inherent in electricity and magnetism to make its measurements. This leads us to measurements of time as provided by a clock. All clocks use oscillations of known intervals to measure time. This can be demonstrated in the fact that a sun-dial uses the oscillations as provided by the rotation cycle of the Earth, grandfather clocks use pendulums, and light clocks bounce light between two reflective surfaces. There are many more mechanisms that clocks use to measure time, such as oscillations as provided by crystals, but the point is that they are all based on mechanisms that oscillate. Oscillation in itself is motion and, more specifically, it is motion that repeats with a specified frequency. It is because time can only be measured with motion that motion must be inherent in time. The same statements are true for motion through any other spatial dimension. We can use oscillation to measure our speed along the x axis the same way a speedometer uses the oscillations of the vehicle's wheels to measure the speed of the vehicle. But, if the vehicle always had a constant velocity along the x axis, then we could also measure physical processes in the vehicle in relation to the vehicle's x position. However, we have the freedom to change our speed and direction along the x axis, making this pseudo-temporal dimension unordered. The physical nature of time seems to be one where motion is the only attribute inherent in the phenomena and it is restricted to moving forward along the temporal dimension. If time is motion no different than motion in other spatial dimensions, then how can we expect to time travel to a past that only exists as a memory or to a future that will exist as a memory? We would have moved away from this point in time and would have not made it to a point in the future. If time travel was possible, then I would have to currently exist at all points in time from birth to death. This is because if I could time travel, then it would not be possible for me to take the mass-energy of the entire universe with me and arrange it the way it was back then or will be in the future. Plus, this behaviour is not true for any other spatial dimension. I may have existed at location zero on the x axis, but I am no longer at that position. I have moved on and when I go to visit location zero on the x axis, I find that it is not that same as before. There is always something different such as new cars in the parking lot. Furthermore, If all things exist currently at all points in time, then wouldn't the past and future attract gravitationally? Time may not flow linearly but surely we only exist at a given point in time and not simultaneously at all points. From this view I suggest that time travel to a memory of the past or to a memory that will exist in the future is impossible. However, traveling to a point in time that is parallel to ours may reveal a new view of our universe. These temporally displaced universes would move through time at the same rate as we do, except they are ahead or behind us along the temporal dimension. We could fast forward or rewind time in all instances and show that each universe would have its own unique history, etc... But I have not taken GR into account, so I am looking for people to disprove this view or support it and perhaps we all can learn something to the nature of time.

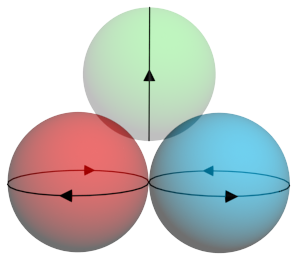
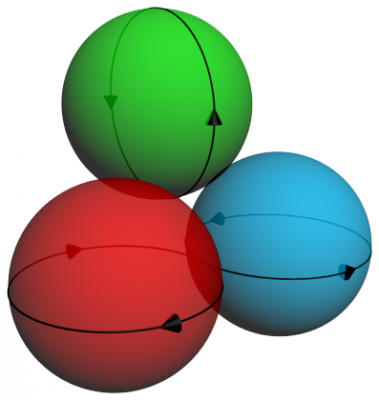
I didn't get to see the original documents, but from reading through the comments I figured I'd draw a few figures showing how three spheres could spin together. You can see the green sphere is spinning upwards. This is similiar to a horizontal gear rotating a vertical gear.

After some considerable thought about a post I made in response to, Check my equation of I x F = E, I decided to follow up with a question about the possibility of quantized length. The question that is posed is one that asks whether there is merit in the notion of quantized space versus analog space and uses the Lorentz factor in regards to length contraction as a basis for the argument. We know that we cannot reach the speed of light due to the definitions in relativity. The Lorentz contraction states that if a body moved at the speed of light relative to an observer, then it would appear to have its length contracted to zero along the direction of motion as seen by the observer. [math]L'=L \sqrt{1-\frac{v^{2}}{c^{2}}}[/math] When [math]v=c[/math], we get: [math]L'=L \sqrt{1-\frac{c^{2}}{c^{2}}}=0[/math] However, we also know that a body in motion would reflect or emit light along each and every position along its trajectory. Therefore, the photons emanating from a body along the collapsed length would still exist and be observable. I realize that it is an extreme leap to go from this view to one where the Lorentz factor is not entirely correct. But if there does exist some smallest quantized length, then a body would not necessarily contract to a zero length at the speed of light. The mathematics that could support this is as follows: If [math]L'\ne0[/math] when [math]v=c[/math], then the Lorentz factor would be off by some factor [math]F[/math], such that: [math]L'=L \sqrt{1-\frac{c^{2}}{c^{2}}\times F}=L\times l[/math] Solving for [math]F[/math] we get: [math]F=1-l^{2}[/math] Substituting this result back into the modified equation we arrive at: [math]L'=L \sqrt{1-\frac{v^{2}}{c^{2}}\times (1-l^{2})}=L \sqrt{1-\frac{(v+v l)(v-v l)}{c^{2}}}[/math] We can see that if [math]l=0[/math], then we get back the original equation: [math]L'=L \sqrt{1-\frac{(v+v\times 0)(v-v\times 0)}{c^{2}}}=L \sqrt{1-\frac{v^{2}}{c^{2}}}[/math] And when [math]v=0[/math], the modified equation yields the same result as the original equation: [math]L'=L \sqrt{1-\frac{(0+0\times l)(0-0\times l)}{c^{2}}}=L[/math] The only difference lies in how it treats space in regards to relativistic velocities near or at the speed of light such that when [math]v=c[/math] we get: [math]L'=L \sqrt{1-\frac{(c+c\times l)(c-c\times l)}{c^{2}}}=L\times l[/math] Thus if [math]l[/math] is extremely small, then it would not even be observed as it would fall outside of our current abilities to detect and measure this hypothetical quantized length. If we solve for [math]l[/math] algebraically we get: [math]l=\frac{\sqrt{v^{2}-c^{2}(1-\frac{L'^{2}}{L^{2}})}}{v} [/math] From this result we can infer two things: 1.) We can measure [math]l[/math] by evaluating the Lorentz contraction for a body that is approaching the speed of light such that: [math]l=\frac{\sqrt{c^{2}-c^{2}(1-\frac{L'^{2}}{L^{2}})}}{c}=\frac{L'}{L} [/math] 2.) Having the velocity ending up in the denominator would suggest that it is impossible to truly be at rest. This is in complete agreement with our observations because all things are in motion. This result seems logical in the aspect that it is easier for me to accept a consequence that I can never truly be stationary versus one that states I would be contracted to an improbable zero length. The question now remains if this idea has any merit?

I'm sorry. I wasn't clear as to the type of scaling I was referring to. I was talking about inverse proportional scaling of the form 1 / n. The Lorentz contraction exhibits similiar behavior. I fully understand that the mathematics support the observed length decreasing to zero at the speed of light. I'm just making a statement about infinitesimals. Given my above explanation about the existence of some distance in between any two infinitesimal points, and that the Lorentz contraction is not a subtractive operation, that a body in motion being observed scales along the direction of motion such that we still see the object as we should, albeit a distorted view, and not some fractional portion of it such as the front when we should see both the front and the side of the body in motion. So the faster you go relative to an observer in a different frame of reference, the smaller you appear to that observer and vice-versa. If we place everything we know about Physics aside except for the fact that a body in motion, such as a spaceship, will always reflect or emit light along each and every point that it traverses along its trajectory. Then if said body could somehow move at the speed of light relative to an observer, the observer should be able to record the information of the photons emanating from the body at each and every point along the body's observed path. However, the Lorentz contraction states that the observer would not be able to see the object's length along the direction of motion because it has been contracted to zero and this seems to be a contradiction to the logic stated previously. So this is where I have the problem and suggest that a photon must have some observable "length" for this special theoretical case. Now I understand that relativity solves this by only allowing particles with zero mass to obtain this speed. These particles are said to have relativistic mass, but this mass does not directly equate to the type of mass we have being comprised of atoms. Therefore bodies such as space ships will never be fully contracted as they can never reach the speed of light. But back to the original point I was trying to make. Intuition tells me, although it may be wrong, that we would still observe a single strip of photons along the direction of motion if a body could move at the speed of light. Therefore, the length is not zero but that of an infinitesimal value that is expressed as a physical constant. I am also aware that the dimensional analysis of this hypothetical "l" universal constant reveals that it is unitless. The fact that it is multiplied by L to arrive at L' preserves the unit of measurement. This would allow for the body to maintain some detectable length along the direction of motion, and all of the information contained within the photons along this length would be conserved, even though they would all be compressed into a single strip of photons equal to the object's length perpendicular to the direction of forward motion. This suggests that infinitesimals are inherent in the structure of space-time. The confusion comes from the fact that our mathematics is simplified to treat all particles as point-particles that exhibit fields that have no definite length, and as in the case of gravity propagates through the entirety of space. I'm suggesting that infinitesimals play thier role in the structure of space-time to preserve the information of the photons emanating from a body in motion relative to an observer because all of the photons that have their positions transformed due to the Lorentz contraction would still exist even if the equations predict that they would be compressed to a zero length. Thus, this hypothetical universal constant "l" is an information conservation mechanism and as shown in the mathematics from my original post, preserves the original Lorentz contraction equation and therefore affects the underlying Lorentz factor. This is because if "l" is truly non-existent, zero, we get back the original equation. If "l" does exist, then we no longer obtain infinite density due to finite mass being concentrated in a dimensionless point because the fields exhibited by point particles can never trully collapse to a zero length due to relativistic velocities. There is support for the existence of this universal infinitesimal constant, "l", because the Lorentz factor can be expressed using infinite series operators. This means that the Lorentz factor can be viewed as a recursive process that is expressed as the number of recursions approach infinity. It is important to understand that infinitesimal numbers exist from -infinity to +infinity. This means that they can approach the limits of transcendentals, reals, integers, etc... The fact that we can derive huerisic shortcuts in mathematics for recursive processes, finite or infinite, is just a simplification of the underlying nature of the processes for which we are deriving relationships. When dealing with processes that have limits that approach infinity, we must accept the consecquence that the result we get is a limit and not an actual value that represent the true nature of the result. This is because we can never reach infinity. Therefore there will always be an infinitesimal that is present that accounts for uncertainty in measurements and provides a mechanism for chaos to emerge from an ordered system and vice-versa. I believe that infinitesimals will be at the heart of the Grand Unification Theory and it will most likely be based on equations that describe quantum gravity as an infinitely recursive fractal pattern similar to how the recusive Fibonacci sequence seems to govern the pattern that life on Earth uses to build its structures. But it may be the case that I do not full understand what it means to have a perceived length of zero. I am only a software engineer that develops class 2 electronic gaming devices using C++ and C# on Windows and Linux (Gentoo Rules). C# allows me to quickly create utility apps. So I will admit that I could be completely wrong as I only took the necessary Physics courses as required by my chosen field. But I am heading back to college this fall after eight - nine years in the field to work towards a degree in Physics. I'm particularly interested in ring singularities and theories on time. I can't wait to apply my knowledge of computer science to model complex quantum processes. P.S. Aspergers and Dyslexia can be blessing and a pain in the ass. The means that you will never get a short answer from me and that there is a chance that I will reverse words, concepts, and numbers without realizing it. I am also moving this thread as AJB suggested to the Lorentz group to see how far we can take this topic. So you can follow me there if you like.

That's awesome. Helped me realize what I was imagining in my head, except I had no way of describing it properly. I got a lot to think about and even more to learn. Thank You!

Sorry, I'm new here. Didn't mean to hijack this thread. Just giving an opinion and I do understand what you are saying. I actually completed finite calculus and numerical analysis. I was just trying to give an explanation and opinion that the OP may relate too. Your statement to deriving infinitesimals is a relative matter. You can either start from the small and work towards the large or vice-versa. However, the approach you have stated is considered proper compared to the one I demonstrated. On the topic of the Lorentz contraction, I am new to this area in physics. I am currently going back to college to work on a degree in Physics and look forward to exploring all of these areas.

A more accurate and correct statement would be: An infinite length divided into an infinite number of segments would produce a segment length of one. This is in relation to the set of integers, Z. If we take each segment and sub-divide them into an infinite number of parts, then each part will be equal to the infinitesimal 1 / Infinity. This is in relation to the set of real numbers, R. Some will argue that this length is zero. However, a decimal with an infinite number of zeroes followed by a one in not equal to an infinite number of zeroes followed by a zero. The proof lies in the fact that two points will always have some length seperating them. If two consecutive real numbers did not have a length seperating them, then we would get: Sigma {1 -> Inf, l} = 0 where l = 0, is the length seperating two points. However, if l = 1 / Infinity we get: Sigma {1 -> Inf, l} = 1 Now for any finite measurable length L, that we apply the same process, we get l = L / Inf. Therefore the infinite sum of the infinitesimal is: Sigma {1 -> Inf, l} = L It is because of the mathematics shown above, that no two points will ever be able to come together due to scaling. This is one of the problems I have with the Lorentz factor because it is a scaling effect that states that relative length will be zero if an object traveled at the speed of light. Since photons travel at the speed of light, am I to assert that they have no relative length in the direction of forward motion? I will for now concede to Einstein, however I believe that photons have some infinitesimal length in the direction of forward motion. But I cannot prove this even through I have a highly speculative modification to the Lorentz factor that accounts for this. Accepted length contraction equation L' = L Sqrt(1 - v^2 / c^2) L' = 0 when v = c However a photon should have some size, maybe it dont. But the equation for this would be: l = L Sqrt(1 - (c ^ 2 / c^2) * F) where l is an unknown universal constant that represents the relative length of a photon and F is an unknown factor that is applied to the Lorentz contraction. Solving for F we get: F = 1 - l^2 plugging this back into the modified equation we get: L' = L Sqrt(1 - (v^2 / c^2)(1 - l^2) when v = 0 we still get L' = L. But, when v = c we would get: L' = l If l is extremely small, then we would not observe the effects of l as both, accepted and modified, equations produce near identical results except when dealing with relative length at the speed of light. If l is truly zero, we get the original equation back. Factoring the modified equation we arrive at: L' = L Sqrt(1 - (v+vl)(v-vl) / c^2) Enjoy!

Hello everyone. My name is Cleveland. I am a software engineer and specialize in multimedia applications using C++. I have over 9 years professional experience in the casino gaming industry and have over 20 slot machines that I have designed and implemented; all of which are class 2 gaming devices. I am going back to college this fall to obtain a degree in Physics. I am not sure where I want to specialize, but I'm really excited about being able to model complex physical systems in the near future. The reason why I have joined this forum is to find people to discuss a theory I have recently developed relating to special relativity. I am not looking for ignorant remarks, or put downs. I can find those just about anywhere. What I do want, is to engage in an intellectual conversation as to why I may be right or wrong. I have a feeling that I am correct. However, I am open to any and all debates and will withdraw my arguments if someone can convince me of a proof as to why I am incorrect. I will post a link to my write up, once I locate the appropriate section to post a link.