Everything posted by Genady
-
Quantum Computing, exercise 2.3
Continuing the same theme: My answers: a. 3/4, 1/4 b. 1/4, 3/4 c. 1/2, 1/2 d. 1/2, 1/2 e. 1/2, 1/2 f. 1/2, 1/2 g. 1/8*(4+2√3), 1/8*(4-2√3) Does it look right? I am not sure what they mean "describe possible measurement outcomes". I think that the outcomes are just Yes or No for whatever is measured each time.
-
Quantum Computing, exercise 2.3
-
Suggestions for method to determine if AI is intelligent.
Mattock, sheep, rocket, clock?
-
Airlines And Other Private Companies Going Into The Space Industry
E.g., OceanGate Inc. did not take such a risk.
-
Quantum Computing, exercise 2.3
Exercise 2.4: Which of the states in 2.3 are superpositions with respect to the Hadamard basis (|+〉, |−〉), and which are not? My answer: Superpositions: b, c, d, e. Not superpositions: a, f. OK?
-
Quantum Computing, exercise 2.3
From Rieffel, Eleanor G.; Polak, Wolfgang H.. Quantum Computing: A Gentle Introduction: Which states are superpositions with respect to the standard basis, and which are not? For each state that is a superposition, give a basis with respect to which it is not a superposition. a. |+〉 b. 1/√2 (|+〉 + |−〉) c. 1/√2 (|+〉 − |−〉) d. √3/2 |+〉 − 1/2 |−〉 e. 1/√2 (|i〉 − |−i〉) f. 1/√2 (|0〉 − |1〉) *Definitions: |+〉 = 1/√2 (|0〉 + |1〉) |−〉 = 1/√2 (|0〉 − |1〉) |i〉 = 1/√2 (|0〉 + i|1〉) |−i〉 = 1/√2 (|0〉 −i|1〉) My answers: a. superposition; basis: |+〉, |−〉 b. not a superposition c. not a superposition d. superposition; basis: √3/2 |+〉 − 1/2 |−〉, 1/2 |+〉 + √3/2 |−〉 e. not a superposition f. superposition; basis: |+〉, |−〉 Agree?
-
Quantum Computing, exercise 2.1
Sorry, I forgot to say where the exercise came from: Rieffel, Eleanor G.; Polak, Wolfgang H. Quantum Computing: A Gentle Introduction.
-
Quantum Computing, exercise 2.2
Which pairs of expressions for quantum states represent the same state? For those pairs that represent different states, describe a measurement for which the probabilities of the two outcomes differ for the two states and give these probabilities. (My answers in red.) a. |0〉 and −|0〉 same b. |1〉 and i|1〉 same c. 1/√2 (|0〉 + |1〉) and 1/√2 (−|0〉 + i|1〉) different; measure 1/√2 (|0〉 + |1〉); probabilities 1 and 0 d. 1/√2 (|0〉 + |1〉) and 1/√2 (|0〉 − |1〉) different; measure 1/√2 (|0〉 + |1〉); probabilities 1 and 0 e. 1/√2 (|0〉 − |1〉) and 1/√2 (|1〉 − |0〉) same f. 1/√2 (|0〉 + i|1〉) and 1/√2 (i|1〉 − |0〉) different; measure 1/√2 (|0〉 + i|1〉); probabilities 1 and 0 g. 1/√2 (|+〉 + |−〉) and |0〉 same h. 1/√2 (|i〉 − |−i〉) and |1〉 same i. 1/√2 (|i〉 + |−i〉) and 1/√2 (|−〉 + |+〉) same j. 1/√2 (|0〉 + eiπ/4 |1〉) and 1/√2 (e−iπ/4 |0〉 + |1〉) same *Definitions: |+〉 = 1/√2 (|0〉 + |1〉) |−〉 = 1/√2 (|0〉 − |1〉) |i〉 = 1/√2 (|0〉 + i|1〉) |−i〉 = 1/√2 (|0〉 −i|1〉) [Rieffel, Eleanor G.; Polak, Wolfgang H.. Quantum Computing: A Gentle Introduction. The MIT Press.] Is everything OK?
-
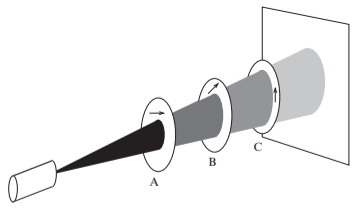
Quantum Computing, exercise 2.1
Only the relative angles matter, don't they? A and C are orthogonal, and B is at the angle θ to A. Yes, this is what they mean, I am sure.
-
Quantum Computing, exercise 2.1
Let the direction |v〉 of polaroid B’s preferred axis be given as a function of θ, |v〉 = cosθ|→〉 + sinθ|↑〉 and suppose that the polaroids A and C remain horizontally and vertically polarized as shown. What fraction of photons reach the screen? Assume that each photon generated by the laser pointer has random polarization. My answer is 1/2*cos2θ*sin2θ. Any objections?
- image test
-
Fuel consumption as an area
Thank you. This goes towards EV. I do, so this goes towards EV. This needs to be considered. Thank you.
-
Fuel consumption as an area
Does it matter that our air temp is around 27-320C year around?
-
Fuel consumption as an area
Almost all my trips are quite short, 2-5 miles each. I guess, battery recharge time would not be an issue in this case. How else would EV and IC cars compare in such use?
-
Are West Europe countries are second class countries in Today's world?
Not counting some overseas municipalities.
-
Fuel consumption as an area
It works the other way around as well: Area as a fuel consumption.
-
The Nobel Prize for Physics has been awarded
What does it mean? How do the moving electrons appear?
-
Fuel consumption as an area
Another example, Hubble parameter in cosmology. Its units are speed per distance, which is 1/time, which is units of frequency. It does not make the Hubble parameter a frequency of anything. Even if one expresses it in Hz.
-
The Nobel Prize for Physics has been awarded
It is an amazing achievement. Did they see anything unexpected?
-
Fuel consumption as an area
So far, it's obvious.
-
precalculus
It looked so to me, as well.
-
Why does fine-tunning for life suggest a multiverse?
I don't think so. For example, in any universe, one could pick a unit of time and then define a unit of distance as the distance which is covered by light in that unit of time. In these units, the speed of light is 1. E.g., 1 year for time and 1 light-year for distance: c = 1 lyr/year = 1. The same works for other units, such as defining degree temperature to make the Boltzmann constant equal to 1, etc. It could be the cause if we discover that these two numbers have to be equal because of some dynamic symmetry, for example. You might not call it a cause in such case, but it could be the only value that allows solution of an equation. Simply put, my hypothesis is that the parameter values cannot be different, like the value of number pi cannot be different.
-
Can the existence of the Graviton be discounted ?
AFAIK, gravitons would be real particles in gravitational radiation, i.e., gravitational waves. But gravitational waves originate outside of the black hole's horizons, so the OP question does not apply.
-
Can the existence of the Graviton be discounted ?
Black hole can be, in principle, charged. A charged nonrotating black hole creates a static electric field outside its event horizon.
-
Can the existence of the Graviton be discounted ?
I don't think so.