steveupson

At the risk of being accused of another thread hijack, I am going to put in my two cents, mainly because nobody has mentioned how a meter is currently defined in SI units (or, if they did, I missed it.) For the past couple of years, the meter is defined in terms of speed of light, or in other words, the unit is the distance that light travels in something like 3(10^-8)seconds someone needs to check that because I'm still having difficultly adjusting to the metric system, i know a foot is the distance light travels in one ns. The old Heathkit oscilloscopes had timing delays that were just long rraces runing back and forth on a pcb. They were able to promote this long trace as a "look ahead" feature because it allowed the sweep to trigger ahead of the vertical amplifier such that no information was lost at the beginning of the sweep which is where glitches liked to hide. So the standard unit that we use to define distance is based on light travel time in a vacuum. So, if we take another look at the coordinate system for your block universe (3D+t ), we know that traditionally the 3D are the spatial coordinates or distance along the orthogonal x-,y-,z-axes; or, in other words. we have light travel time in x, y and z directions for three of our coordinates and then time t for the fourth. so, since the speed of light has been adopted for the relativistic constant, we have two trains, with one being 10 times as many femtoseconds long as the other, such that one is 10m long and the other is 100m. This type of coordinate system seems totally ill-suited for relativistic spacetime since establishing proper time is critical to being able to observe the property of distance. I just thought that i would mention this since no one else has noted it here. You used the word "direction in your response and that was all tha it took for me too instantly connect my pet theory with your op. in case you haven't heard, my pet theory is that "direction is a physical property that can be observed independently from time or distance. This "heresy' has become a taboo subject at many fora that cater to this kind of dialog that we are having here, But that's a whole nuther topic having more to do with religious dogma than science, although one could argue that religion has become a mercenary science science deducated to the redistribution of capital. Ive been working with others to initiate development of a new model which we are calling timespace, Mathematically, the major difference is that we've begun using direction rather than distance as the metric. jIt is worth pointing out that direction isn't really limited by the speed of light. For example, if you were to shine a spotlight at the moon, and then pass your finger in front of the beam, there is no limit to how fast the shadow could travel across the lunar surface. Of course the photons are governed by universal speed limit, but the shadow isn't. In the timespace model, there is no block universe. Instead, the timespace universe contains only energy and time, that's all there is; energy can be present in the form of bound energy (matter) or unbound energy (light) as weird as it sounds, there are many deep symmetries between the new model and the standard model. Almost every observable phenomonon can be explained using only the law of conservation, theory of relativity, and the equivalence principle. In the new model, there are three base quantities:(1) time, (2)distance, and (3) direction. That's right in this new look around, directoin is a quantity having a scalar value instead of being a vector quantity based on ratios between lengths. to support the argumant that direction is a property, I'll say a few words about chirality, sure, the standard model can explain chirality as handedness whatever that means does the standard model tell us how chirality comes about? is there somewhere in the universe where it might be reversed such tha when you pass a magnet through a loop of wire that the electric current flows backwards to what we are used to? inthe new model, it is slightly more accessable, because the three base quanities can be set up conceptionally like ro sham bo, and the question becomes analogous to what happens if steel scissors can cut rock or rock can puncture paper, and so on. Having written this, it's my guess that you are more likely to run across someone who plays rock paper scissors backwards than you are to run across a place where electricity flows backwards, (opposite chirality). Also, and this may sound impertinent to those members who are sick and tired of reading my thoughts about my pet theory. But, It is CRITICAL to observe that chirality.. ,whatever it is, cannot be observed as existing without at least three spatial dimensions. Hmmm three spatial dimensions are required in order to manifest chirality. oh yeah, and chirality needs no additional prooperties or parameters it is a stand-alone phenomonon based solely on direction. oh yeah, welcome to the op and to any new members that aren't familiar with my crack-pottery, umm.. (eccentricities.) let me just say that I feel your frustration with the length contraction question. it seems arbitrary to me that the meter would be based on light travel time instead of basing the second on how long it takes to travel a meter. But ,the history is clear, atomic clocks were developed decades before the meter was ever defined this way. In 2019, I think.

Nice, that makes a lot of sense. It deals with the difference in velocity as if both frames are either moving at different speeds in the same direction, or different speeds in the opposite direction. It doesn't really accommodate for situations where the frames are moving at different speeds in different directions, which is the same issue that you run into with the relativistic Doppler model. haha, this IS fun.

You lost me. The OP begins "I have always considered gravity to be a force..." You seem to be saying the same thing, that mass is an attractive force. I don't think that is correct, although I do agree that electromagnetic force and mechanical force are not the same. A better argument might be that, because of the way the calculus is done (the way that our derived units are calculated), gravity is more akin to acceleration, as expressed by the Equivalence_principle.

The twin paradox is different in a subtle way that you might not see. In Minkowski space we're traveling along a geodesic, while in the twin thought experiment one or both of the twins must make at least one complete turn.

From the wiki: " Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with distance and time coordinates." It looks to me as if we have time and distance twice (in two frames) and that they relate to one another by a direction (hyperbolic angle.) I'm wondering what evidence there is that this direction is the correct direction. I don't think that it's possible to express the correct direction using a tensor at all. By axiomatic definition these things have to be perpendicular to one another, and we know that they aren't or else everything would be just like it is in Newtonian space. Right? How do you think this gets worked out in the model? It really seems to me as if the rapidity is something real, except that it can only be used to express relationships in a single direction. In other words, it's useless for modeling relativistic Doppler effect. The geometry is wrong (not really wrong, it is correct, it's just that it isn't what people think it is) for this purpose. Another type of geometry will be necessary to make a more accurate mathematical representation. Understand that the math and geometry that I'm referring to is based in the same Euclidean 3-space that is familiar to everyone, except that it uses a different metric.

It is currently not known by modern mathematics that the three angles have a relationship with one another. 1) Diameter of the small circle, expressed as an arc length of the sphere 2) Latitude of your feet 3) Direction that you are facing

II don't think that you understand the mathematical issues that are involved. There is an equation that expresses a family of functions. Strange modeled this in mathematica. The tridentity is a different equation. Someone asked what the tridentity is good for, and it allows you to make constructions like one that tells you what direction you're facing when on a small circle on a sphere.

Strange used V to replace upsilon, and L for lambda. Lambda must be within twice upsilon since upsilon is the center of the circle.

.Again, I don't think that you understand the nature of the mathematical issues involved. The forces are not complicated at all, and can be calculated in a very straightforward manner. The mathematical question is about how to determine the kinematics. Or, how can we use vectors to find which direction we're facing from knowing our latitude and the diameter of the circle we're going around.

I don't know why you make that assumption. You're definitely not understanding the mathematical issues involved in this type of problem. I've provided two such examples in this thread already, together with the following statement: "In any event, I think that when we try to solve this type of problem using lines with arrowheads for our symbols we don’t have as much power as we have when we replace those symbols with a plane. That change allows us to do this type of calculation without having to result to the successive approximations that we were using in the first case. I’m pretty sure that within the next few years someone will prove that this type of problem cannot be solved using vector manipulation. But that’s simply a prediction based on what I know about the math, and how the two are substantially different than one another." If you think that I'm mistaken somehow, then show me. Where are the existing equations?

I have a couple of questions about this. I'm understanding that forces come in pairs, or in other words that there isn't a positive charge without a negative charge, and so forth. I have seen some information on zero-point energy and I'm wondering if this has anything to do with what you're talking about when you mention an interaction that is unopposed. I've always thought about this in a different context, such as comparing the charge of the substrate to the charge of the electrons and holes in a semiconductior. I don' t think that this is what you mean, and I wonder if you can provide some more information on how the calculus is done. Also, what is the difference between what you're saying about "Rapidity" and what another member might say about a "Pet Theory" where direction is a quantity? It sure does sound similar, if it isn't the same thing exactly. What is this "Rapidity" made from? I would assume that since it is expressed as a hyperbolic, that it's related somehow to the concept of "orthogonality" that we have always used to distinguish Newtonian 3D from GR 4D. I think that if I could understand exactly what you mean in this post that it would go a long way towards showing why a certain "Pet Theory" is somehow incorrect. Also, how is "freefall" defined mathematically? What physical quantities (or if we're using dimensional analysis, what dimensions) is it made from? These are the questions that I have a lot of difficulty understanding. I think that the "Pet Theory" resolves or answers these questions in a very solid way, mathematically speaking. I think that the "Pet Theory" shows that the geometry of spacetime is not treated correctly when we use the traditional methods for modeling the Newtonian 3D component. It seems to be the right approach, it just seems to me to be incorrect due to the inability to specify "what" is being modeled differently when we add "Rapidity" to the model. It changes something, but do you know what it is that is being changed? Can you describe what this thing is that is different after we add "Rapidity," and can you say why it is something other than a difference in direction?

The two systems are not in communication with one another at this time. There is someone working on trying to relate them to one another through creation of physical models for force or energy. Until we can add distance to the geometry, I think these two things will not transform from one to the other. There's a lot of work to be done yet, in order to answer this question.

There's a series of interactive videos that allow you to view the math, and play with the visuals. It's a pretty good way to get a handle on the math that is involved. https://eater.net/quaternions

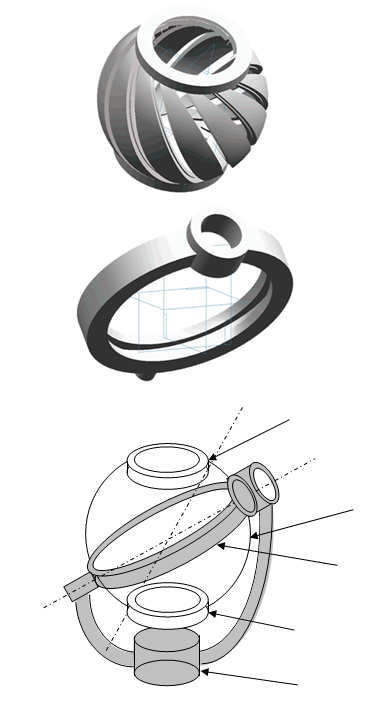
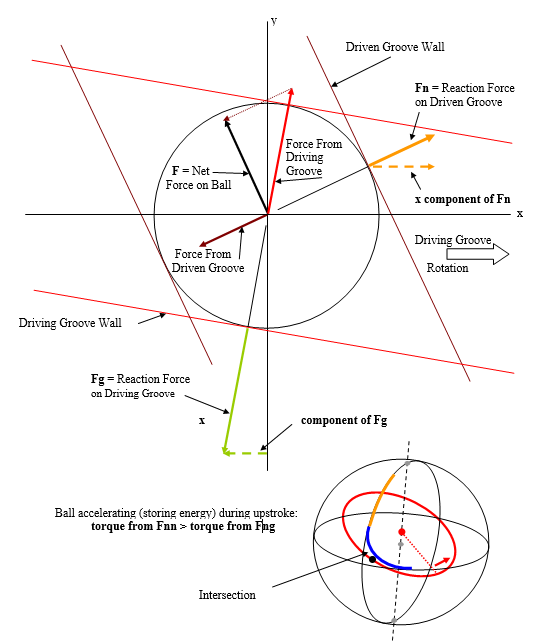
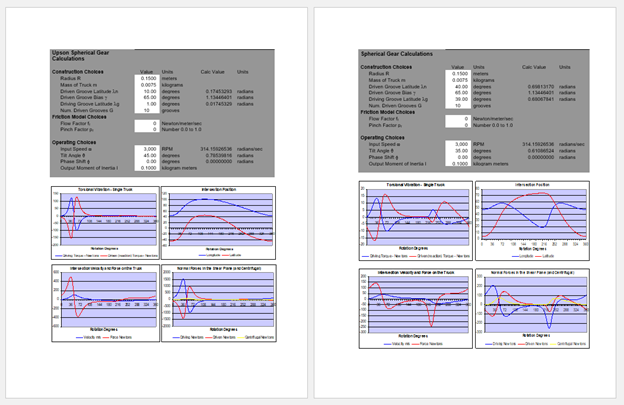
Oh, ok. I think you might be getting this result because you’re no longer on the circle. The extent of the circle is from zero at the north pole, to 2V at its southernmost point, so the range of L is 0,2V. This is because whatever the latitude of the southernmost point of the circle is, the midpoint of this latitude will be the latitude where we would find the circle center, if we were to dig deep enough. I want to look into this further, but that might take a little while. Here’s a brief history of the project that led us to where we are. We were trying to perform a dynamic analysis of the behavior of a small steel ball that is trapped in the intersection of two grooves on the surface of two spheres. As the two spheres are rotated relative to one another, the steel ball trapped in the intersection will be forced to travel along the grooves in a prescribed manner. In order to do the analysis, we needed to determine the kinematics of the system. In the 3D illustration of the model, only the part of the sphere that represents the groove is shown for the outer groove, and this groove is able to be tilted in a manner such that its relationship the other groove is variable. For the analysis, we held the inner sphere stationary (which we call the driven groove Dn) while we turned the outer groove (which we call the driving groove Dg.) At different inclinations of the driving groove, we get different reactions from the ball trapped in the intersection. This next illustration shows how we went about resolving the forces on the ball. During a complete rotation, the ball would travel up the driven groove, stop, then travel back down the driven groove to its original position, experiencing different rates of acceleration, or in other words, storing and returning energy. To model the forces, we chose the “shear plane” for our reference frame. The forces in the shear plane are modeled in the diagram below. The shear plane is tangent to the spheres at the intersection of the grooves. Everything is rather mundane up to this point. Then, in order to determine the path of the ball in the intersection, it is necessary to know the slope of the grooves as they move past one another, and to relate this slope back to the rotation of the driving groove. Initially we tried to resolve these slopes using spherical trigonometry, without success. We gave up in frustration with that idea, and instead we used finite rotations in order to relate the two slopes back to the axis of rotation. We would perform a series of three rotations (projections) such that we were in the shear plane, move the ball according to the two slopes, then reverse the three discrete rotations back to the original frame, advance the model a tiny bit, and repeat. The process called for a series of successive approximations in order to find the slopes each time the model was advanced. This is because of the fact that the two small circles that parameterize the two different slopes were different radii. There was no other solution to the problem. These notes show the transforms that we used. pg transform.pdf These notes show the bookkeeping that was required in order to do the calculus. Theory of Operation.pdf Here are typical results we obtained from our model in the Win 96 version of Excel. Many years later, while looking through our notes, I came across a cryptic illustration that was based on how we originally approached the problem. In our naiveite we had stumbled across a completely different approach. That’s when I started posting online to try to solicit help with the project. You’re one of the people who has been along for the whole ride, since those early days. In any event, I think that when we try to solve this type of problem using lines with arrowheads for our symbols we don’t have as much power as we have when we replace those symbols with a plane. That change allows us to do this type of calculation without having to result to the successive approximations that we were using in the first case. I’m pretty sure that within the next few years someone will prove that this type of problem cannot be solved using vector manipulation. But that’s simply a prediction based on what I know about the math, and how the two are substantially different than one another. I'm not quite sure what you mean about chirality being a rabbit hole. Don't tell me that you don't believe in chirality...

I think that the sign will represent chirality in the completed geometry (when distance is derived.) And as far as it being very complicated, I can't really offer any apologies for that. The fact that vector manipulation won't readily solve the problem should provide ample illustration of its worth. (Actually, we've had excellent results using vector calculus in order to solve this type of problem. The difference is that instead of having to integrate many discrete rotations or projections, here we have a smooth function that performs the same task. Mathematically, for some reason, the two give the same result for this problem, but I don't think that this is the case with relativistic problems. The two methods should definitely give different results because they use completely different methods.) I'm not really that good with algebra, but the equation is the resulting function from combining two simultaneous equations that relate alpha and lambda to another variable phi. It's in the proof. Do the math. How many times do I have to tell you that as far as I can tell it is completely impossible to understand any of this without doing the math. 1. The alpha = 0° result means that you are facing normal to the meridian plane. Or, the tangent to the circle where you are standing is parallel to the surface normal to the meridian plane. There is no angle between them. The two planes that set up this relationship are the one that is tangent to the cone having the small circle as its base, and the meridian plane, where both are intersecting at your feet. 2. I'm not sure what that means, or what you are referring to. If we use negative values for some of the inputs then the outputs are also negative. That could be what you're talking about. Maybe? There is a complicated issue of how to keep track of the sign for alpha. I may have gotten that particular calculation crossed up so that I am actually calculating the complementary angle for alpha instead of alpha, but it really is the best that I can do considering my very limited abilities with algebra. I wasn't able to come up with the actual formula that is being used. It was someone (Did) from mathstackexchange who helped with that. The simultaneous equations that give the parameterization of alpha are: As a check, we were able to compare results of the formula to the results that we already had from the original mathematica model. This gave us a high degree of confidence that the formula is correct. I don't know if you recall, but there was quite a bit of discussion over the concept that mathematica was able to create the model without knowing the equation. I'm sure that this is related to the issue stated above about how we were able to solve these problems long before we had this formula. Also, in addition to alpha=f(lambda), these same equations can be combined in order to produce the tridentity: