Mordred

You can but keep in mind that dissertation was back in the late 80's lol and publishing requirements will vary depending on the publisher. Swansont for example has a peer reviewed paper on arxiv. I studied it a few years back.

Ok let's do a personal experienced example. I once wrote a dissertation paper using quintessence for inflation. At that time period there were dozens of quintessence inflationary models kicking around. The two most popular classes of inflationary models were Chaotic eternal inflation and quintessence. (Everyone believed in one or the other). My disseration at that time was a good match to COBE findings. Then WMAP took measurement of the CMB and with its findings my dissertation instantly became null and void as the equations state I had could not be fixed to account for the required E-folds. Theory done proven incorrect with one dataset. Later confirmed by other datasets. All it takes is 1 reasobably conclusive test to invalid a given theory. That's the process. It doesn't matter how strongly myself or others believe in a theory. Tests and evidence can trump any theory if it doesn't match up to observational and experimental evidence. The last couple of years I have been researching Higgs inflation so far I know I can get write a paper on it that would match current observational evidence however if new evidence becomes available it could just as easily trump the theory I'm working on.

Another good example of shoddy science is perpetual motion machines. You sometimes see papers that seem well written and have all the required details. However if the experiment cannot be reproduced by other independent examiners. You know something is fishy. If others perform the same experiment then the two experiments should match within reasonable approximation allowing for potential error margins.

That I would agree with. Regardless of the science if the science doesn't match evidence. Then the theory gets changed to account or gets dropped.

What I gather from this thread is that bias isn't science but the opinion of the scientific process itself. The way this thread has gone in circles supports that it's the bias of opinion of the scientific method itself

Yes I know for a fact that time dilation cannot account for the cosmological constant. When you do the math you will find that you get the wrong ratios of change. You will also discover as Migl mentioned Newtons Shell theorem that time dilation isn't involved when you have a homogeneous and isotropic mass distribution. Let's do a simple example if you use recessive velocity from Hubbles Law \[v_{r}=H_0d\] and apply that velocity term to the time dilation formula you will think it will work out. However once you get to the Hubble horizon it approach infinity. The Observable universe itself is far larger than the Hubble horizon. The recessive velocity formula will have a value for recessive velocity of 2.3 c. Thankfully recessive velocity is not a true velocity but an apparent velocity due to separation distance. As our time dilation formula would break down when velocity is greater than c. Leading to causality issues. Our light cone would be restricted to the Hubble horizon. The recessive velocity equals c at the hubble horizon. We observe beyond that. Does that help ?

If you know the frequencies your trying to detect you might also want to look into band pass circuits to filter out unwanted signals. Also RF signals are maximally detected via an an antenna at 1/4 wavelength. If your antenna picks up half the wavelength you get refective currents that will degrade your signal and cause equipment damage. Optionally 3/4 wavelength is just as effective as 1/4. If you could provide more detail such as frequencies involved we may be able to help fine tune your components.

Agreed that wiki article is lousy on the correct details. It's almost as if someone who wrote it was half guessing what's involved. It's likely that it was written by someone who knows how an engineer uses it but doesn't understand how it's used in particle physics.

I think your issue is not realizing that the linear translations are between groups. For example the last example I gave is translating between SU(2) to SU(3). The original groups contain the information your looking for. The LCTs is how to take that information from one group to another group. Correct and what you are doing is using the correlations to establish how to transform from one group or map to another.

That description above isn't too bad you have the basic idea. Lets expand on it the BB at \(10^{-43}\) s was in a hot, dense state. Now the FLRW metric uses those equations of state above, which are thermodynamic relations between the kinetic energy and pressure terms of the multi-particle field. Matter has no pressure term as it doesn't have sufficient momentum to generate pressure. However relativistic particles do have the momentum terms. ie photons and neutrinos. The FLRW metric treats expansion as an ideal fluid with adiabatic and isentropic expansion. The Cosmological principle tells us this state is homogeneous and isotropic. as the universe expands then accordingly the temperature and pressure decrease as a result. In point of detail the inverse of the scale factor will give you the CMB blackbody temperature at that value of "a"=scale factor. The equations of state in the above link give the different momentum to pressure relations for radiation, Lambda and matter.

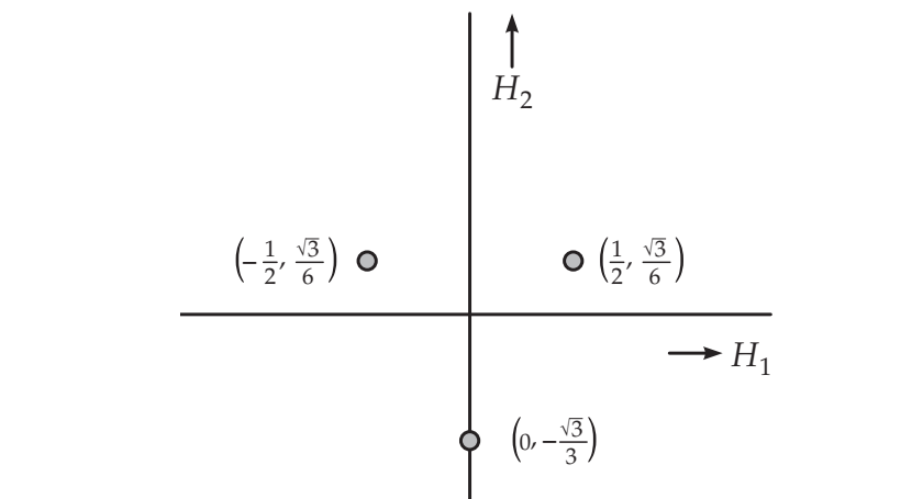
Understood and I'm glad you recognize that these symmetry relations are internal symmetries and not spacetime symmetries. To understand spin I would recommend taking time studying Cartan subalgebra. Here is the trick The synmmetry representations are expressed according to weights which correspond to eugenvalues. For example the quantum numbers of angular momentum all have their own weight under lie algebra however they also have their own weight diagram. (aka root diagram) for example the spin j of a particle is given by \[U(\vec{\theta})=e\frac{i}{\hbar}\vec{\theta}\cdot \hat{J}\] where \(\hat{J}\) is the three angular momentum operators whose representation will be given by \(2J+1\) dimensional and \(\vec{\theta}\) are the 3 parameters gives \[e^{\frac{i}{\hbar}\vec{\theta}\cdot J}|jm\rangle=\sum_{n}=-jC_nJn\rangle\] imposing \[U(\vec{\theta-1})U(\vec{\phi}(\theta_1\theta_2))\] results in subalgebra SU(2) \[[J_i,j_j]=i\hbar\epsilon_{i,j,k}J_k\] where raising and lowering operators are defined \[J_\pm=(J_1\pm iJ_2)/11/2\] there is the spin operations you mentioned. for SU(3) Now the Gell Mann matrices above has three basis states. \[|\Lambda\mu_1\rangle=\begin{pmatrix}1\\0\\0\end{pmatrix}\] \[|\Lambda\mu_2\rangle=\begin{pmatrix}0\\1\\0\end{pmatrix}\] \[|\Lambda\mu_2\rangle=\begin{pmatrix}0\\0\\1\end{pmatrix}\] where \({\mu_1,\mu_2,\mu_3}\) are called two component weight vectors given by eugenvalues \(H_1=\lambda_3/2\) and \(H_2=\lambda_8/2\) see Gell-Mann matrices above \[\Lambda \mu_1=(1/2,\sqrt{3}/6):|\Lambda \mu_2\rangle=(-1/2,\sqrt{3}/6):|\Lambda \mu_3\rangle=(0,-\sqrt{3}3/3)\] the above is your Dynkan spin representation of SU(3) SU(3) has an eight dimensional root diagram which is an adjoint representation not shown above https://en.wikipedia.org/wiki/Adjoint_representation#Structure_constants for the OP understandably this will likely be over your head but also for other readers Group theory is a theory of representations these representations gives us tools to find and organize symmetry relations and antisymmetric relations. These representations have their own algebras (lie Algebra, Clifford algebra, Cartan algebra, etc,etc). They often use internal symmetries which can be thought of as (mathematical symmetries) though these can be also be physical quantities or probability quantities. In particle physics the state is a typically a probability wavefunction same for QFT. Lie algebra involves raising and lowering of Operators an operator has a requirement of being a minimal 1 quanta of action. (Langrangian) Now we also have group symmetries homomorphism> a linear map between two lie algebras is homomorphic if it is non invertable.(useful for bosons aka symmetric) An isomophism is invertable (fermions aka antisymmetric). Now lie algebras have subalgebras. Dynkin diagrams help us organize all the simple and semi-simple representations. In a sense it forms an atlas of our mappings. So SU(3) has 8 generators The Gell Mann matrices above. Each matric has its own root and hence its own weight that has its own weight diagram (aka root diagram which is a map). These maps can be a sub group of a larger group and vice versa. Dynkin diagrams also provide these details.

Wouldn't change anything as SU(n) is a subgroup of Sl(n,C) which is a subgroup of GL(N,C). The problem with renormalization for gravity isn't that we cannot renormalize for normal gravity ranges. You have two types of divergence. IR (infrared) ie divide by zero. This is easily fixed and already implemented. The other end of the spectrum is ultraviolet divergence. (We don't have any known limit to the mass term ) so the singularity condition of the BB and the singularity of a BH. This is where the problem occurs. In math speak via QFT we can renormslize for 1 loop integrals but cannot renormalize for 2 loop liberals and higher. The mathematical method used won't change this as the problem is where to set the upper limit.

So let me understand this correctly you have some physics idea but when you attempt to apply known physics find that you cannot do so which technically should invalidate the idea but you also consider that a form of bias as opposed to proper methodology. Do I have that correct ?

Your welcome I wouldn't use the reference 6 it's not a method to learn particle physics from. While the LCTs and the SL(2C) group is part of particle physics the chart in reference 6 was generated using the SM Unitary groups. The groups the SM model primarily uses is U(1), SU(2) and SU(3). Focus on those groups first as well as the Poincare group. SO(3.1). The above is the groups for the SM model the LCTs while has uses that wiki page doesn't describe correctly where they are used in particle physics. Instead it's reference is a method in development It is the Unitary groups mentioned above that you will find in any particle physics textbook and not what is described by the LCT wiki link. Dynkin diagrams are advanced beyond the introductory level. While the Unitary groups will provide the details for another representation (Feymann path integrals)

for reference https://www.tigercheng.xyz/Dynkin_Diagrams.pdf see 4.2 for rank 2 roots. which I supplied the relations above. The roots can be thought of as 2 dimensional vectors in a plane some other helpful diagrams involving other groups as well. https://web.ma.utexas.edu/users/vandyke/notes/261_notes/lecture19.pdf this one includes the Coxeter diagrams (they act as symmetry reflections ) well explained in this link https://math.ucr.edu/home/baez/twf_dynkin.pdf hope that helps Edit I too find the 5 dimensional part used in reference 6 of the OPs link a bit fishy going to look into that particular article in greater detail

Lol I think you became too used to Unitary and orthogonal groups. Joigus Would it help to know SO(3.1) and SU(n) are both subgroups of SL(2,c)/Z_2 ? lets start with the following \[sl(2,\mathbb{C})=su(2)\oplus isu(2)\] generators denoted e,f,h [e,f=h] [h,e]=2e [h,f]=-2f the 2C is the linear combination of e,f,h \[\pi (h)=\begin{pmatrix}1&0\\0&-1\end{pmatrix}\] \[\pi( e)=\begin{pmatrix}0&1\\0&0\end{pmatrix}\] \[\pi h=\begin{pmatrix}0&0\\-1&0\end{pmatrix}\] \[f_i,h_i,e_i\] i=1,2,3....r however the set of complex cannot all commute so you need commutations \[[h_ih_j]=0\] \[[h_i,e_j]=A_{ji}e_j\] \[h_i,f_i]=-A_{ji}f_j\] \[[e_i,f_j]=\delta_{ij}h_{ij}\] where \(A_{ij} \) is the Cartan matrix ( I won't go through the ladder operators as they are fairly lengthy) however it can be expressed as \[[h_i,e_i]=\langle\alpha_j\rangle=\frac{2}{\langle\alpha_j,\alpha_j}\langle\alpha_j,\alpha_i\rangle_j=A_{ji}e_j\] \[\begin{pmatrix}2&-1\\-1&2\end{pmatrix}\] the above is for SL(2C) for sl(3,C) the Cartan matrix is an 8 dimensional algebra of rank 2 which means it has a 2 dimensional Cartan sub algebra given as follows \[\pi(t_1)= \begin{pmatrix}0&1&0\\1&0&0\\0&0&0\end{pmatrix}\] \[\pi(t_2)= \begin{pmatrix}0&-i&0\\i&0&0\\0&0&0\end{pmatrix}\] \[\pi(t_3)= \begin{pmatrix}1&0&0\\0&-1&0\\0&0&0\end{pmatrix}\] \[\pi(t_4)= \begin{pmatrix}0&0&1\\0&-1&0\\0&0&0\end{pmatrix}\] \[\pi(t_5) =\begin{pmatrix}0&0&-i\\0&0&0\\i&0&0\end{pmatrix}\] \[\pi(t_6)= \begin{pmatrix}0&0&0\\0&0&1\\0&1&0\end{pmatrix}\] \[\pi(t_7)= \begin{pmatrix}0&0&0\\0&0&-i\\0&i&0\end{pmatrix}\] \[\pi(t_1)=\frac{1}{\sqrt{3}} \begin{pmatrix}0&1&0\\1&0&0\\0&0&-2\end{pmatrix}\] You may note the last is the Gell-Mann matrices if we take the commutator between \(\pi(t_1)\) and \(\pi(t_2)\) we get \([\pi(t_1),\pi(t_2)]=2i\pi(t_3)\) which is familiar in the su(2) algebra. Thus we can define the following \[x_1=\frac{1}{2}t_1\] \[x_2=\frac{1}{2}t_1\] \[x_3=\frac{1}{2}t_3\] \[y_4=\frac{1}{2}t_4\] \[y_5=\frac{1}{2}t_5\] \[z_6=\frac{1}{2}t_6\] \[z_7=\frac{1}{2}t_7\] \[z_8=\frac{1}{\sqrt{3}}t_8\] with change in basis \[e_1=x_1+ix_2\] \[e_2=y_4+iy_5\] \[e_3=z_6+iz_7\] \[f_1=x_1+ix_2\] \[f_2=y_4+iy_5\] \[f_3=z_6+iz_7\] Now I should inform everyone that the basis and coordinates I am describing apply to Dynken diagrams and what I am describing apply to the root diagrams... https://en.wikipedia.org/wiki/Dynkin_diagram the basis above in matrix form is \[\pi(e_1)=\begin{pmatrix}0&1&0\\0&0&0\\0&0&0\end{pmatrix}\] \[\pi(e_2)=\begin{pmatrix}0&0&1\\0&0&0\\0&0&0\end{pmatrix}\] \[\pi(e_1)=\begin{pmatrix}0&0&0\\0&0&1\\0&0&0\end{pmatrix}\] \[\pi(f_1)=\begin{pmatrix}0&0&0\\1&0&0\\0&0&0\end{pmatrix}\] \[\pi(f_2)=\begin{pmatrix}0&0&0\\0&0&0\\1&0&0\end{pmatrix}\] \[\pi(f_3)=\begin{pmatrix}0&0&0\\0&0&0\\0&1&0\end{pmatrix}\] \[\pi(x_3)=\frac{1}{2}\begin{pmatrix}1&1&0\\0&-1&0\\0&0&0\end{pmatrix}\] \[\pi(z_8)=\frac{1}{3}\begin{pmatrix}1&0&0\\0&1&0\\0&0&-2\end{pmatrix}\] @joigus That should help better understand the special linear group of Real as well as complex. Now knowing the above applies to Dynken diagrams will also help better understand the validity of the OPs link as well as the methodology. @TheoM Hope this answers your question as well on the validity behind the LCT's and where they are applied in particle physics so yes the link overall you provided is valid

ok well as far as the chart goes the details are correct the main reason why the SM model uses the SU(n) groups is that tis group is compact which becomes important for renormalization as well as Feymann path integrals. the SL(n) group is not compact which can lead to issues with renormalization even though both groups are closed groups the isomorphism for the Lorentz/Poincare group for example is \[S0(3.1)\simeq Sl(2,\mathbb{C})/\mathbb{Z}_2\] spinors are defined to transform under the action of the \( SL2(\mathbb{C}\) group. So yes that link is accurate where it gets used as opposed to other group types depends on the state being described. However as shown here \[S0(3.1)\simeq Sl(2,\mathbb{C}/\mathbb){Z}_2\] you can have isomorphisms with other groups the isomorphisms for SU(N) to the SL(2,c) group can be found here which is what reference 6 of the link you gave which corresponds to the chart you posted employs further details here https://diposit.ub.edu/dspace/bitstream/2445/121903/2/memoria.pdf I should also forewarn you though that the Schrodinger equation of QM is not Lorentz invariant although the Dirac equations are. The operators used in QM (position and momentum) are not employed in QFT (field and momentum). QM uses the Klein Gordon equations which are Lorentz invariant. This is the purpose of reference 6 ": Linear Canonical Transformations (LCTs) are known in signal processing and optics as the generalization of certain useful integral transforms. In quantum theory, they can be identified as the linear transformations which keep invariant the canonical commutation relations characterizing the coordinates and momenta operators. In this work, the possibility of considering LCTs to be the elements of a symmetry group for relativistic quantum physics is studied using the principle of covariance" reference 6 here https://arxiv.org/pdf/1804.10053

As someone who develops physics theories I employ known physics in 35 years I have never found any need not to employ known physics. If I cannot employ known physics to develop a theory that tells me there is something wrong with my theory. Do you consider that a form of bias ? (Keep in mind I am a firm believer that any theory I develop I put every effort I can to disprove my own theory) lol in point of detail I am extremely good at proving my own theories invalid or inaccurate.

So what is your question ? The group is often useful for linear symmetry relations.

Well in terms of emergent there are numerous papers of emergent spacetime as well as emergent quantum fields. However how emergence is typically treated is from other field geometries example Calibi Yau spacetime from string theory. The more typical papers for emergent spacetime are typically string theory or ADS/CFT formalism We have to be careful here as emergent doesn't necessarily mean come into existence but rather specific relations and dimensionality ie 5d or higher dimension models leading to emerging 4d spacetime relations. The same can result from lower dimension theories emerging to higher dimension relations. I should add a field can be any collection of values (mathematical or physical) under a geometric treatment. In QFT for example the creation/annihilation operators employ the field as an operator. In a sense the field can propagate the creation/annihilation operators. The operators operate on the propogators. (An operator is has a minimal of 1 quanta of action ) this is the minimum energy level for an operator. (A propogator can have any value but can be below a quanta of action ) example virtual photons and gauge bosons. Aka the internal wavy lines of Feymann path integrals. The operators would be the external lines.

No time dilation would not explain dark energy but don't feel bad this conjecture has already been considered and tested for. Back when we first discovered the accelerating expansion physicists looked at the possibility of being observer effect due to time dilation. The problem is the cosmological constant is too constant to be explained by the non linear curve of time dilation formulas. This turned out not to work but at least the good news is that your idea had merit. To add detail it was low redshift values for the late time accelerating portion of expansion ( Lambda dominant era) compared to the deceleration portion(matter dominant era) that showed that time dilation could not explain the cosmological constant. ( the transition between matter dominant and Lambda dominant occurs roughly when the universe is between 6 and 7 billion years old.) It is the redshift variations (which incorporates time dilation effects) that showed that time dilation could not explain the cosmological term w=-1. In point of detail it was the redshift data between this transition which became further evidence supporting the existence of the cosmological term when initially it was felt it would support an observer effect due to time dilation. ( you get similar results from luminosity distance and angular size via distance relations ). We have used all three methods above to try to eliminate or validate the cosmological term at various redshift distances and at different matter/radiation densities

As I understand it, it's due tonhigh fat and low moisture content.

No problem it's easy to forget details when thinking of GR QFT etc lol. It may help to recall that it is the stress energy momentum tensor that spacetime how to curve and that spacetime curvature describes particle paths (geodesics). Hence the use of the (ct) interval is incredibly useful.

A common misconception spacetime isn't really something that forms spacetime has no fabric like substance. It's simply a geometric volume with time having dimensionality of length via the ct interval. So in order to have fields you require a volume for the fields to reside in. All forms of mass energy contribute to spacetime curvature. If there is no curvature spacetime is still just the 4d volume.

I seem to recall someone mentioning a reference for the nuke method in regards to the radiation vs kinetic shock wave you get for atmospheric explosion that last link highlights thar detail. Just in case anyone missed that.