Everything posted by Orion1
-
Toy model black holes per galaxy average number...
I am attempting to look within the rather large error bars for the estimates of the number of black holes in a galaxy. The calculated solutions are within the parameters of the mainstream conclusion. Revision complete for year 2020 data... [math]\color{blue}{\text{Planck satellite baryonic cosmological composition parameter:} \; (\text{ref. 1, pg. 11, ref. 2, pg. 3})}[/math] [math]\Omega_{b} = 0.0495[/math] [math]\;[/math] [math]\color{blue}{\text{Black holes cosmological composition parameter:} \; (\text{ref. 2, pg. 3})}[/math] [math]\Omega_{bh} = 0.00007[/math] [math]\;[/math] [math]\color{blue}{\text{Solar mass:} \; (\text{ref. 3})}[/math] [math]M_{\odot} = 1.9885 \cdot 10^{30} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Milky Way galaxy mass:} \; (\text{ref. 4, pg. 1})}[/math] [math]M_{mw} = 1.260 \cdot 10^{12} \cdot M_{\odot} = 2.506 \cdot 10^{42} \; \text{kg}[/math] [math]\boxed{M_{mw} = 2.506 \cdot 10^{42} \; \text{kg}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model stellar baryon composition:} \; (\text{ref. 2, pg. 3})}[/math] [math]\Omega_s = \left(\Omega_{ms} + \Omega_{wd} + \Omega_{ns} \right) = 2.460 \cdot 10^{-3}[/math] [math]\boxed{\Omega_s = 2.460 \cdot 10^{-3}}[/math] [math]\Omega_{ms} - \text{main sequence stars cosmological composition parameter}[/math] [math]\Omega_{wd} - \text{white dwarf stars cosmological composition parameter}[/math] [math]\Omega_{ns}- \text{neutron stars cosmological composition parameter}[/math] [math]\;[/math] [math]\color{blue}{\text{Total stellar class number:} \; (\text{ref. 5})}[/math] [math]n_c = 7[/math] [math]\color{blue}{\text{key: 1 O, 2 B, 3 A, 4 F, 5 G, 6 K, 7 M}}[/math] [math]\Omega_f - \text{main sequence stars stellar class fraction}[/math] [math]N_s - \text{total observable stellar number}[/math] [math]M_s - \text{main sequence stellar mass}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model average stellar mass:} \; (\text{ref. 5})}[/math] [math]M_{as} = \frac{1}{N_s} \sum_{n = 1}^{n_c} \Omega_f\left(n \right) N_s M_s\left(n \right) = \sum_{n = 1}^{n_c} \Omega_f\left(n \right) M_s\left(n \right) = 0.219 \cdot M_{\odot} \rightarrow 0.595 \cdot M_{\odot}[/math] [math]\boxed{M_{as} = \sum_{n = 1}^{n_c} \Omega_f\left(n \right) M_s\left(n \right)} \; \; \; n_c = 7[/math] [math]\boxed{M_{as} = \left(0.219 \rightarrow 0.595 \right) \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Toy model average stellar mass upper bound limit:}}[/math] [math]\boxed{M_{as} = 1.184 \cdot 10^{30} \; \text{kg}}[/math] [math]\color{blue}{\text{Observabe universe average stellar mass:} \; (\text{ref. 6, pg. 20})}[/math] [math]M_{as} = 0.6 \cdot M_{\odot} = 1.193 \cdot 10^{30} \; \text{kg}[/math] [math]M_{as} = 1.193 \cdot 10^{30} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way stars per galaxy average number:}}[/math] [math]\frac{N_s}{N_g} = \frac{\Omega_s M_{mw}}{\Omega_b M_{as}} = 1.053 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}}[/math] [math]\boxed{\frac{N_s}{N_g} = \frac{\Omega_s M_{mw}}{\Omega_b M_{as}}}[/math] [math]\boxed{\frac{N_s}{N_g} = 1.053 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe stars per galaxy average number:} \; (\text{ref. 7, ref. 8})}[/math] [math]\frac{N_s}{N_g} = 1.500 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy total stellar number:} \; (\text{ref. 8})}[/math] [math]\frac{N_s}{N_g} = 2.500 \cdot 10^{11} \pm 1.500 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}} \; \; \; \; \; \frac{N_s}{N_g} = \left(1.000 \cdot 10^{11} \rightarrow 4.000 \cdot 10^{11} \right) \; \frac{\text{stars}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way black holes per galaxy average number integration via substitution:}}[/math] [math]\frac{N_{bh}}{N_{g}} = \frac{\Omega_{bh}}{\Omega_{b}} \left(\frac{N_{s}}{N_{g}} \right) = \frac{\Omega_{bh}}{\Omega_{b}} \left(\frac{\Omega_s M_{mw}}{\Omega_b M_{as}} \right) = \frac{\Omega_{bh} \Omega_s M_{mw}}{\Omega_{b}^{2} M_{as}} = 1.489 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = \frac{\Omega_{bh} \Omega_s M_{mw}}{\Omega_{b}^{2} M_{as}}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = 1.489 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\;[/math] [math]\color{blue}{\text{Synthetic catalog black holes per galaxy average number:} \; (\text{ref. 9, pg. 1})}[/math] [math]\frac{N_{bh}}{N_g} = 1.293 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = \frac{\Omega_{bh}}{\Omega_{b}} \left(\frac{N_{s}}{N_{g}} \right)}[/math] [math]\boxed{\frac{N_{bh}}{N_g} = \left(1.414 \cdot 10^{8} \rightarrow 5.657 \cdot 10^{8} \right) \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way galaxy average black hole mass integration via substitution:}}[/math] [math]M_{bh} = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left(\frac{N_{g}}{N_{bh}} \right) = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left[\frac{\Omega_{b}^{2} M_{as}}{\Omega_{bh} \Omega_s M_{mw}} \right] = \left(\frac{\Omega_{b}}{\Omega_{s}} \right) M_{as} = 2.379 \cdot 10^{31} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = \left(\frac{\Omega_{b}}{\Omega_{s}} \right) M_{as}}[/math] [math]\boxed{M_{bh} = 2.382 \cdot 10^{31} \; \text{kg}}[/math] [math]\boxed{M_{bh} = 11.979\cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Calculated synthetic catalog Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left(\frac{N_{g}}{N_{bh}} \right)}[/math] [math]\boxed{M_{bh} = 2.741 \cdot 10^{31} \; \text{kg}}[/math] [math]\boxed{M_{bh} = 13.783 \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Synthetic catalog Milky Way galaxy average black hole mass:} \; (\text{ref. 9, pg. 1})}[/math] [math]M_{bh} = 2.784 \cdot 10^{31} \; \text{kg}[/math] [math]M_{bh} = 14.000 \cdot M_{\odot}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy average black hole mass integration via substitution:}}[/math] [math]M_{bh} = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left(\frac{N_{g}}{N_{bh}} \right) = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left[\frac{\Omega_{b}}{\Omega_{bh}} \left(\frac{N_{g}}{N_{s}} \right) \right] = M_{mw} \left(\frac{N_{g}}{N_{s}} \right) = 6.265 \cdot 10^{30} \; \text{kg} \rightarrow 2.506 \cdot 10^{31} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = M_{mw} \left(\frac{N_{g}}{N_{s}} \right)}[/math] [math]\boxed{M_{bh} = \left(6.265 \cdot 10^{30} \; \text{kg} \rightarrow 2.506 \cdot 10^{31} \; \text{kg} \right)}[/math] [math]\boxed{M_{bh} = \left(3.151 \rightarrow 12.603 \right) \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Black hole mass spectrum domain:} \; (\text{ref. 10, ref. 11})}[/math] [math]\boxed{2.27 \cdot M_{\odot} \leq M_{bh} \leq 36 \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Calculation results summary:}}[/math] [math]\color{blue}{\text{Toy model Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = 1.489 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\color{blue}{\text{Synthetic catalog black holes per galaxy average number:}}[/math] [math]\frac{N_{bh}}{N_g} = 1.293 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\color{blue}{\text{Observable universe Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_g} = \left(1.414 \cdot 10^{8} \rightarrow 5.657 \cdot 10^{8} \right) \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\color{blue}{\text{Toy model Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = 11.979 \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Calculated synthetic catalog Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = 13.783 \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Synthetic catalog Milky Way galaxy average black hole mass:}}[/math] [math]M_{bh} = 14.000 \cdot M_{\odot}[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = \left(3.151 \rightarrow 12.603 \right) \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Toy model average stellar mass:}}[/math] [math]\boxed{M_{as} = \left(0.219 \rightarrow 0.595 \right) \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Any discussions and/or peer reviews about this specific topic thread?}}[/math] [math]\;[/math] "This above all: to thine own self be true, And it must follow, as the night the day, Thou canst not then be false to any man." - Polonius [math]\;[/math] Reference: Planck 2013 results. XVI. Cosmological parameters: (ref. 1) https://arxiv.org/pdf/1303.5076.pdf The Cosmic Energy Inventory: (ref. 2) http://arxiv.org/pdf/astro-ph/0406095v2.pdf Wikipedia - Sun Sol: (ref. 3) https://en.wikipedia.org/wiki/Sun Mass models of the Milky Way: (ref. 4) http://arxiv.org/pdf/1102.4340v1 Wikipedia - Stellar classification - Harvard spectral classification: (ref. 5) https://en.wikipedia.org/wiki/Stellar_classification#Harvard_spectral_classification On The Mass Distribution Of Stars...: (ref. 6) http://www.doiserbia.nb.rs/img/doi/1450-698X/2006/1450-698X0672017N.pdf Wikipedia - Observable universe total stellar number: (ref. 7) https://en.wikipedia.org/wiki/Star Distribution Wikipedia - Milky Way Galaxy: (ref. 8) https://en.wikipedia.org/wiki/Milky Way Synthetic catalog of black holes in the Milky Way (2020): (ref. 9) https://arxiv.org/pdf/1908.08775.pdf Wikipedia - Tolman-Oppenheimer-Volkoff limit: (ref. 10) https://en.wikipedia.org/wiki/Tolman-Oppenheimer-Volkoff_limit Wikipedia - Black hole: (ref. 11) https://en.wikipedia.org/wiki/Black_hole#Detection_of_gravitational_waves_from_merging_black_holes
-
Toy model black holes per galaxy average number...
Affirmative, that OP post 1, reference 1 link has since been broken after it was posted on September 4, 2019. The updated reference link is still available on post 3, reference 1, and in Reference here. "Once we accept our limits, we go beyond them." - Albert Einstein Reference: Planck 2013 results. XVI. Cosmological parameters: https://arxiv.org/pdf/1303.5076.pdf Toy model black holes per galaxy average number - post 3 - Orion1: https://www.scienceforums.net/topic/120012-toy-model-black-holes-per-galaxy-average-number/?do=findComment&comment=1192794
-
Toy model black holes per galaxy average number...
we do have others that even dispute their existence. There is no misunderstanding, I was merely responding that there is in fact a long standing dispute if black holes exist or not. Any observational evidence for their existence was not available until Cygnus X-1 was discovered in 1964. For any scientific claim, the burden of proof is on the individual making such a claim. Therefore, absent any observational evidence, the rational default position is that they are merely potentially falsifiable "theoretical artifacts" until experimental observational evidence becomes available. Even Albert Einstein doubted the existence of black holes. In a paper written in 1939, Albert Einstein attempted to reject the notion of black holes that his theory of general relativity and gravity, published more than two decades earlier, seemed to predict. Einstein denied several times that black holes could form. In 1939 he published a paper that argues that a star collapsing would spin faster and faster, spinning at the speed of light with infinite energy well before the point where it is about to collapse into a Schwarzchild singularity, or black hole. "The essential result of this investigation is a clear understanding as to why the "Schwarzschild singularities" do not exist in physical reality. Although the theory given here treats only clusters whose particles move along circular paths it does not seem to be subject to reasonable doubt that mote general cases will have analogous results. The "Schwarzschild singularity" does not appear for the reason that matter cannot be concentrated arbitrarily. And this is due to the fact that otherwise the constituting particles would reach the velocity of light." - Albert Einstein Reference: Wikipedia - Cygnus X-1: https://en.wikipedia.org/wiki/Cygnus_X-1 Wikipedia - List of black_holes: https://en.wikipedia.org/wiki/List_of_black_holes The Racah Institute of Physics - On A Stationary System With Spherical Symmetry Consisting Of Many Gravitating Masses - Albert Einstein - 1939: http://old.phys.huji.ac.il/~barak_kol/Courses/Black-holes/reading-papers/Einstein1939.pdf
-
Toy model black holes per galaxy average number...
Orion1 wants his work to be analyzed and shot at.... unlike many. Peer review discussions have proven to be more valuable in improving my research, equations, calculations and solutions. Confucius says: Man with watch always knows the time. Man with two watches is never sure. And two men each with a watch, and time becomes relative. I am not qualified to review your estimates nor the methodology you are using, its just that on many occasions, we do have others that even dispute their existence. The ability to multiply and divide math is the only qualification to review my estimates. I disagree that my equations are incomprehensible. There is observational evidence for the existence of black holes. On 10 April 2019 an image was released of a black hole, which is seen in magnified fashion because the light paths near the event horizon are highly bent. The dark shadow in the middle results from light paths absorbed by the black hole. The image is in false color, as the detected light halo in this image is not in the visible spectrum, but radio waves. The Event Horizon Telescope (EHT), is an active program that directly observes the immediate environment of the event horizon of black holes, such as the black hole at the centre of the Milky Way. In April 2017, The Event Horizon Telescope (EHT) began observation of the black hole in the center of Messier 87. Prior to this, in 2015, the The Event Horizon Telescope (EHT) detected magnetic fields just outside the event horizon of Sagittarius A*. On 14 September 2015 the LIGO gravitational wave observatory made the first-ever successful direct observation of gravitational waves. The signal was consistent with theoretical predictions for the gravitational waves produced by the merger of two black holes: one with about 36 solar masses, and the other around 29 solar masses. This observation provides the most concrete evidence for the existence of black holes to date. if your estimates are correct and there are far more BH's then thought, could that constitute the Dark Matter problem? (or part thereof) MACHO's come to mind. Negative, in my opinion black holes do not constitute dark matter. Although the population densities and masses seem high, their overall compositional parameter is low compared to the dark matter compositional parameter: Black holes cosmological composition parameter: [math]\Omega_{bh} = 0.00007[/math] Dark matter cosmological composition parameter: [math]\Omega_{dm} = 0.268[/math] This means that 0.007% of everything is composed of black holes, while 26.8% of everything is composed of dark matter. Dark energy composition plus dark matter composition plus baryonic matter composition equals one. [math]\Omega_{\Lambda} + \Omega_{dm} + \Omega_{b} = 1[/math] 68.25% + 26.8% + 4.95% = 100% In my opinion, the "Bullet Cluster" rules out all candidate theories for dark matter, except for, (and possibly non-baryonic), extremely small mass quantum particles. Several groups have searched for MACHOs by searching for the microlensing amplification of light. These groups have ruled out dark matter being explained by MACHOs with mass in the range 1×10−8 solar masses (0.3 lunar masses) to 100 solar masses. These searches have ruled out the possibility that these objects make up a significant fraction of dark matter in our galaxy. Observations using the Hubble Space Telescope's NICMOS instrument showed that less than one percent of the halo mass is composed of red dwarfs. This corresponds to a negligible fraction of the dark matter halo mass. Therefore, the missing mass problem is not solved by MACHOs. How many BH's out there may not have accretion disks? (having been around long enough to consume all matter/energy within its region) is another consideration I think. This is a dynamic question that depends mostly on the environment that the black hole was generated in, its age, and the availability of baryonic matter in that environment as accretion fuel. I would expect newly generated black holes to have a bright accretion disk and polar jets, and as time passes, the disk and jets fade away from fuel exhaustion, with the remaining residual baryonic matter being driven away by the accretion and polar jet radiation. However, black holes in binary systems could receive an unstable continuous supply of fuel from their companion star's solar wind, or if within proximity, accreted directly from the companion star's surface, possibly producing intermittent high energy x-ray and gamma radiation bursts. According to the "Synthetic catalog of black holes in the Milky Way", there are 9.3 million black holes in binary systems: Black Holes in binary systems: [math]N_{bhb} = 9.3 \cdot 10^{6} \; \text{black holes}[/math] "Only when it is dark enough can you see the stars." - Martin Luther King, Jr. Reference: Wikipedia - Black hole - Observational evidence/Accretion of matter: https://en.wikipedia.org/wiki/Black_hole#Observational_evidence https://en.wikipedia.org/wiki/Black_hole#Accretion_of_matter Wikipedia - Dark matter https://en.wikipedia.org/wiki/Dark_matter Wikipedia - Bullet Cluster: https://en.wikipedia.org/wiki/Bullet_Cluster Wikipedia - Massive compact halo object https://en.wikipedia.org/wiki/Massive_compact_halo_object Synthetic catalog of black holes in the Milky Way: https://arxiv.org/pdf/1908.08775.pdf
-
Toy model black holes per galaxy average number...
Peer review discussions have proven to be more valuable in improving my research, equations, calculations and solutions than a blog. Time: The indefinite continued progress of existence and events in the past, present, and future regarded as a whole. "travel through space and time" The definition seems simple enough. I am attempting to look within the rather large error bars for the estimates of the number of black holes in a galaxy. The calculated solutions are within the parameters of the mainstream conclusion. The difference is that the prior required only a single equation, while the latter required a sophisticated computer algorithm. Does not oppose but validates the mainstream picture, however, this offers an alternative solution to mainstream physics. In terms of stellar astrophysics, the estimate numbers are equivalent to an arrow hitting a target bulls-eye. Time is the indefinite continued progress of existence and events in the past, present, and future regarded as a whole. I am attempting to look within the rather large error bars for the estimates of the number of black holes in a galaxy. There is no discussion requirement to follow external sources, those external sources exist because the burden of proof is mine. However, anyone interested in astrophysics would be depleting themselves of interesting information by not researching available resource materials. "I would rather have questions that can't be answered than answers that can't be questioned." - Richard Feynman
- Test #1 Quote to start
-
Toy model black holes per galaxy average number...
[math]\color{blue}{\text{Planck satellite baryonic cosmological composition parameter:} \; (\text{ref. 1, pg. 11, ref. 2, pg. 3})}[/math] [math]\Omega_{b} = 0.0495[/math] [math]\;[/math] [math]\color{blue}{\text{Black holes cosmological composition parameter:} \; (\text{ref. 2, pg. 3})}[/math] [math]\Omega_{bh} = 0.00007[/math] [math]\;[/math] [math]\color{blue}{\text{Solar mass:} \; (\text{ref. 3})}[/math] [math]M_{\odot} = 1.9885 \cdot 10^{30} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Milky Way galaxy mass:} \; (\text{ref. 4, pg. 1})}[/math] [math]M_{mw} = 1.260 \cdot 10^{12} \cdot M_{\odot} = 2.506 \cdot 10^{42} \; \text{kg}[/math] [math]\boxed{M_{mw} = 2.506 \cdot 10^{42} \; \text{kg}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model stellar baryon composition:} \; (\text{ref. 2, pg. 3})}[/math] [math]\Omega_s = \left(\Omega_{ms} + \Omega_{wd} + \Omega_{ns} \right) = 2.460 \cdot 10^{-3}[/math] [math]\boxed{\Omega_s = 2.460 \cdot 10^{-3}}[/math] [math]\;[/math] [math]\color{blue}{\text{Total stellar class number:} \; (\text{ref. 5})}[/math] [math]n_c = 7[/math] [math]\color{blue}{\text{key: 1 O, 2 B, 3 A, 4 F, 5 G, 6 K, 7 M}}[/math] [math]\Omega_f - \text{main sequence stars stellar class fraction}[/math] [math]N_s - \text{total observable stellar number}[/math] [math]M_s - \text{main sequence stellar mass}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model average stellar mass:} \; (\text{ref. 5})}[/math] [math]M_{as} = \frac{1}{N_s} \sum_{n = 1}^{n_c} \Omega_f\left(n \right) N_s M_s\left(n \right) = \sum_{n = 1}^{n_c} \Omega_f\left(n \right) M_s\left(n \right) = 0.219 \cdot M_{\odot} \rightarrow 0.595 \cdot M_{\odot}[/math] [math]\boxed{M_{as} = \sum_{n = 1}^{n_c} \Omega_f\left(n \right) M_s\left(n \right)} \; \; \; n_c = 7[/math] [math]\boxed{M_{as} = \left(0.219 \rightarrow 0.595 \right) \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Toy model average stellar mass upper bound limit:}}[/math] [math]\boxed{M_{as} = 1.184 \cdot 10^{30} \; \text{kg}}[/math] [math]\color{blue}{\text{Observabe universe average stellar mass:} \; (\text{ref. 6, pg. 20})}[/math] [math]M_{as} = 0.6 \cdot M_{\odot} = 1.193 \cdot 10^{30} \; \text{kg}[/math] [math]M_{as} = 1.193 \cdot 10^{30} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way stars per galaxy average number:}}[/math] [math]\frac{N_s}{N_g} = \frac{\Omega_s M_{mw}}{\Omega_b M_{as}} = 1.053 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}}[/math] [math]\boxed{\frac{N_s}{N_g} = \frac{\Omega_s M_{mw}}{\Omega_b M_{as}}}[/math] [math]\boxed{\frac{N_s}{N_g} = 1.053 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe stars per galaxy average number:} \; (\text{ref. 7, ref. 8})}[/math] [math]\frac{N_s}{N_g} = 1.500 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy total stellar number:} \; (\text{ref. 8})}[/math] [math]\frac{N_s}{N_g} = 2.500 \cdot 10^{11} \pm 1.500 \cdot 10^{11} \; \frac{\text{stars}}{\text{galaxy}} \; \; \; \; \; \frac{N_s}{N_g} = \left(1.000 \cdot 10^{11} \rightarrow 4.000 \cdot 10^{11} \right) \; \frac{\text{stars}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way black holes per galaxy average number integration via substitution:}}[/math] [math]\frac{N_{bh}}{N_{g}} = \frac{\Omega_{bh}}{\Omega_{b}} \left(\frac{N_{s}}{N_{g}} \right) = \frac{\Omega_{bh}}{\Omega_{b}} \left(\frac{\Omega_s M_{mw}}{\Omega_b M_{as}} \right) = \frac{\Omega_{bh} \Omega_s M_{mw}}{\Omega_{b}^{2} M_{as}} = 1.489 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = \frac{\Omega_{bh} \Omega_s M_{mw}}{\Omega_{b}^{2} M_{as}}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = 1.489 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\;[/math] [math]\color{blue}{\text{Synthetic catalog black holes per galaxy average number:} \; (\text{ref. 9, pg. 1})}[/math] [math]\frac{N_{bh}}{N_g} = 1.693 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = \frac{\Omega_{bh}}{\Omega_{b}} \left(\frac{N_{s}}{N_{g}} \right)}[/math] [math]\boxed{\frac{N_{bh}}{N_g} = \left(1.414 \cdot 10^{8} \rightarrow 5.657 \cdot 10^{8} \right) \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way galaxy average black hole mass integration via substitution:}}[/math] [math]M_{bh} = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left(\frac{N_{g}}{N_{bh}} \right) = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left[\frac{\Omega_{b}^{2} M_{as}}{\Omega_{bh} \Omega_s M_{mw}} \right] = \left(\frac{\Omega_{b}}{\Omega_{s}} \right) M_{as} = 2.379 \cdot 10^{31} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = \left(\frac{\Omega_{b}}{\Omega_{s}} \right) M_{as}}[/math] [math]\boxed{M_{bh} = 2.382 \cdot 10^{31} \; \text{kg}}[/math] [math]\boxed{M_{bh} = 11.979\cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Synthetic catalog Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left(\frac{N_{g}}{N_{bh}} \right)}[/math] [math]\boxed{M_{bh} = 2.093 \cdot 10^{31} \; \text{kg}}[/math] [math]\boxed{M_{bh} = 10.527 \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy average black hole mass integration via substitution:}}[/math] [math]M_{bh} = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left(\frac{N_{g}}{N_{bh}} \right) = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left[\frac{\Omega_{b}}{\Omega_{bh}} \left(\frac{N_{g}}{N_{s}} \right) \right] = M_{mw} \left(\frac{N_{g}}{N_{s}} \right) = 6.265 \cdot 10^{30} \; \text{kg} \rightarrow 2.506 \cdot 10^{31} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = M_{mw} \left(\frac{N_{g}}{N_{s}} \right)}[/math] [math]\boxed{M_{bh} = \left(6.265 \cdot 10^{30} \; \text{kg} \rightarrow 2.506 \cdot 10^{31} \; \text{kg} \right)}[/math] [math]\boxed{M_{bh} = \left(3.151 \rightarrow 12.603 \right) \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Black hole mass spectrum domain:} \; (\text{ref. 10, ref. 11})}[/math] [math]\boxed{2.27 \cdot M_{\odot} \leq M_{bh} \leq 36 \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Calculation results summary:}}[/math] [math]\color{blue}{\text{Toy model Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_{g}} = 1.489 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\color{blue}{\text{Synthetic catalog black holes per galaxy average number:}}[/math] [math]\frac{N_{bh}}{N_g} = 1.693 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\color{blue}{\text{Observable universe Milky Way black holes per galaxy average number:}}[/math] [math]\boxed{\frac{N_{bh}}{N_g} = \left(1.414 \cdot 10^{8} \rightarrow 5.657 \cdot 10^{8} \right) \; \frac{\text{black holes}}{\text{galaxy}}}[/math] [math]\color{blue}{\text{Toy model Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = 11.979 \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Synthetic catalog Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = 10.527 \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Observable universe Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = \left(3.151 \rightarrow 12.603 \right) \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Toy model average stellar mass:}}[/math] [math]\boxed{M_{as} = \left(0.219 \rightarrow 0.595 \right) \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Any discussions and/or peer reviews about this specific topic thread?}}[/math] [math]\;[/math] Reference: Planck 2013 results. XVI. Cosmological parameters: (ref. 1) https://arxiv.org/pdf/1303.5076.pdf The Cosmic Energy Inventory: (ref. 2) http://arxiv.org/pdf/astro-ph/0406095v2.pdf Wikipedia - Sun Sol: (ref. 3) https://en.wikipedia.org/wiki/Sun Mass models of the Milky Way: (ref. 4) http://arxiv.org/pdf/1102.4340v1 Wikipedia - Stellar classification - Harvard spectral classification: (ref. 5) https://en.wikipedia.org/wiki/Stellar_classification#Harvard_spectral_classification On The Mass Distribution Of Stars...: (ref. 6) http://www.doiserbia.nb.rs/img/doi/1450-698X/2006/1450-698X0672017N.pdf Wikipedia - Observable universe total stellar number: (ref. 7) https://en.wikipedia.org/wiki/Star#Distribution Wikipedia - Milky Way Galaxy: (ref. 8) https://en.wikipedia.org/wiki/Milky_Way Synthetic catalog of black holes in the Milky Way: (ref. 9) https://arxiv.org/pdf/1908.08775.pdf Wikipedia - Tolman-Oppenheimer-Volkoff limit: (ref. 10) https://en.wikipedia.org/wiki/Tolman-Oppenheimer-Volkoff_limit Wikipedia - Black hole: (ref. 11) https://en.wikipedia.org/wiki/Black_hole#Detection_of_gravitational_waves_from_merging_black_holes
-
Toy model black holes per galaxy average number...
[math]\color{blue}{\text{Total stellar class number: (ref. 1)}}[/math] [math]n_c = 7[/math] [math]\;[/math] [math]\color{blue}{\text{key: 1 O, 2 B, 3 A, 4 F, 5 G, 6 K, 7 M}}[/math] [math]\Omega_f - \text{main sequence stars stellar class fraction}[/math] [math]N_s - \text{total observable stellar number}[/math] [math]M_s - \text{main sequence stellar mass}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model average stellar mass: (ref. 1)}}[/math] [math]M_{as} = \frac{1}{N_s} \sum_{n = 1}^{n_c} \Omega_f\left(n \right) N_s M_s\left(n \right) = \sum_{n = 1}^{n_c} \Omega_f\left(n \right) M_s\left(n \right) = 0.219 \cdot M_{\odot} \rightarrow 0.595 \cdot M_{\odot}[/math] [math]\boxed{M_{as} = \sum_{n = 1}^{n_c} \Omega_f\left(n \right) M_s\left(n \right)} \; \; \; n_c = 7[/math] [math]\boxed{M_{as} = \left(0.219 \rightarrow 0.595 \right) \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Toy model average stellar mass upper bound limit:}}[/math] [math]\boxed{M_{as} = 1.184 \cdot 10^{30} \; \text{kg}}[/math] [math]\;[/math] [math]\color{blue}{\text{Observabe universe average stellar mass: (ref. 2, pg. 20)}}[/math] [math]M_{as} = 0.6 \cdot M_{\odot} = 1.193 \cdot 10^{30} \; \text{kg}[/math] [math]M_{as} = 1.193 \cdot 10^{30} \; \text{kg}[/math] [math]\;[/math] [math]\color{blue}{\text{Synthetic catalog black holes per galaxy average number: (ref. 3, pg. 1)}}[/math] [math]\frac{N_{bh}}{N_g} = 1.693 \cdot 10^{8} \; \frac{\text{black holes}}{\text{galaxy}}[/math] [math]\;[/math] [math]\color{blue}{\text{Synthetic catalog Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = \frac{\Omega_{bh} M_{mw}}{\Omega_{b}} \left(\frac{N_{g}}{N_{bh}} \right)}[/math] [math]\boxed{M_{bh} = 2.093 \cdot 10^{31} \; \text{kg}}[/math] [math]\boxed{M_{bh} = 10.527 \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Black hole mass spectrum domain: (ref. 4), (ref. 5)}}[/math] [math]\boxed{2.27 \cdot M_{\odot} \leq M_{bh} \leq 36 \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Synthetic catalog Milky Way galaxy average black hole mass:}}[/math] [math]\boxed{M_{bh} = 10.527 \cdot M_{\odot}}[/math] [math]\color{blue}{\text{Toy model average stellar mass:}}[/math] [math]\boxed{M_{as} = \left(0.219 \rightarrow 0.595 \right) \cdot M_{\odot}}[/math] [math]\;[/math] [math]\color{blue}{\text{Any discussions and/or peer reviews about this specific topic thread?}}[/math] [math]\;[/math] Reference: Wikipedia - Stellar classification - Harvard spectral classification: (ref. 1) https://en.wikipedia.org/wiki/Stellar_classification#Harvard_spectral_classification On The Mass Distribution Of Stars...: (ref. 2) http://www.doiserbia.nb.rs/img/doi/1450-698X/2006/1450-698X0672017N.pdf Synthetic catalog of black holes in the Milky Way: (ref. 3) https://arxiv.org/pdf/1908.08775.pdf Wikipedia - Tolman-Oppenheimer-Volkoff limit: (ref. 4) https://en.wikipedia.org/wiki/Tolman-Oppenheimer-Volkoff_limit Wikipedia - Black hole - Detection of gravitation waves from merging black holes: (ref. 5) https://en.wikipedia.org/wiki/Black_hole#Detection_of_gravitational_waves_from_merging_black_holes
-
Cosmic background radiation spectral radiance peak frequencies...
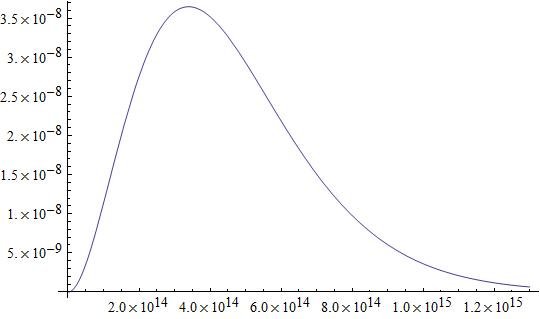
\[\color{blue}{\text{Solar surface photon radiation temperature:} \; (\text{ref. 1})}\] \[T_{\odot} = 5772 \; \text{K}\] \[\color{blue}{\text{Bose-Einstein solar surface photon radiation spectral radiance peak frequency:}}\] \[\boxed{f_{\gamma} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{\odot}}{h}}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\boxed{f_{\gamma} = 3.39332 \cdot 10^{14} \; \text{Hz}}\] \[\boxed{f_{\gamma} = 339.332 \; \text{THz}}\] \[\color{blue}{\text{Calculated solar surface photon radiation spectral radiance peak frequency:} \; (\text{ref. 2})}\] \[f_{\gamma} = \frac{\left[W_{0}\left(-3e^{-3} \right) + 3 \right] k_B T_{\odot}}{h}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[T_{1} = 6000 \; \text{K} \; \; \; f_{\gamma} = 352.735 \; \text{THz}\] \[\color{blue}{\text{Any discussions and/or peer reviews about this specific topic thread?}}\] Reference: Wikipedia - Sun Sol: (ref. 1) https://en.wikipedia.org/wiki/Sun Wikipedia - Wien's displacement law: (ref. 2) https://en.wikipedia.org/wiki/Wien's_displacement_law#Parameterization_by_frequency Wikipedia - Lambert W function: (ref. 3) https://en.wikipedia.org/wiki/Lambert_W_function
-
Cosmic background radiation spectral radiance peak frequencies...
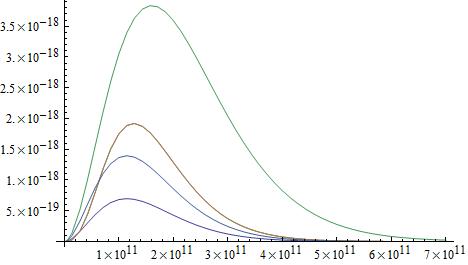
\[\color{blue}{\text{Toy model quantum particle properties chart:}}\] \[\begin{array}{l*{9}{c}r} & \text{identity} & \text{helicity state} & \text{spin} & n_{s} & N_{s} & N_{n} & \text{mass} & \text{type} & \text{spectral radiance peak frequency} \\ b & \text{quinton} & 0 & 0 & 1 & 1 & 1 & 0 & \Lambda & 2.058 \; \text{THz} \\ b & \text{scalaron} & 0 & 0 & 1 & 1 & 1 & 18.658 \; \text{eV} & \phi & 114.366 \; \text{GHz} \\ f & \text{sterile neutrino} & +,- & 1/2 & 2 & 3 & 3 & 8.167 \; \text{eV} & \nu_{s} & 126.915 \; \text{GHz} \\ f & \text{neutrino} & +,- & 1/2 & 2 & 3 & 3 & 0.038 \; \text{eV} & \nu & 126.915 \; \text{GHz} \\ b & \text{photon} & +,- & 1 & 2 & 1 & 2 & 0 & \gamma & 160.229 \; \text{GHz} \\ b & \text{graviton} & +,- & 2 & 2 & 1 & 2 & 0 & \text{G} & 114.366 \; \text{GHz} \\ \end{array}\] \[\color{blue}{\text{Planck's law:}} \; (\color{blue}{\text{ref. 1}})\] \[B\left(f_{\gamma},T_{\gamma} \right) = \frac{N_{\gamma} h f_{\gamma}^{3}}{c^{2} \left(e^{\frac{h f_{\gamma}}{k_{B} T_{\gamma}}} \pm 1 \right)}\] \[\color{blue}{\text{A plus sign in the denominator is a Fermi-Dirac distribution, a minus sign in the denominator is a Bose-Einstein distribution.}}\] \[\color{blue}{\text{+ sign - Fermi-Dirac distribution}}\] \[\color{blue}{\text{- sign - Bose-Einstein distribution}}\] \[\color{blue}{\text{Planck's law energy distribution frequency plot.}} \; (\color{blue}{\text{attached graph 1}})\] \[114.366 \; \text{GHz} \; \; \; 126.915 \; \text{GHz} \; \; \; 160.229 \; \text{GHz}\] \[\color{blue}{\text{Planck's law energy distribution frequency plot.}} \; (\color{blue}{\text{attached graph 2}})\] \[2.058 \; \text{THz}\] \[\color{blue}{\text{In this toy model, some quantum particle radiation distributions are embedded within the photon radiation distribution.}}\] \[\color{blue}{\text{Would a quantum particle radiation distribution embedded within the photon radiation distribution induce cosine anisotropy in the photon radiation?}} \; (\color{blue}{\text{ref. 2}})\] \[\color{blue}{\text{If cosine anisotropy is a detectable amount, is it possible to map cosine anisotropy amounts verses frequency within the photon radiation distribution?}} \; (\color{blue}{\text{ref. 2}})\] \[\color{blue}{\text{Based upon the frequency multi-distribution plot, what frequency domain in the photon radiation distribution would you expect to detect cosine anisotropy?}}\] \[\color{blue}{\text{Any discussions and/or peer reviews about this specific topic thread?}}\] Reference: Wikipedia - Planck's law: (ref. 1) https://en.wikipedia.org/wiki/Planck's_law Wikipedia - Anisotropy - Physics: (ref. 2) https://en.wikipedia.org/wiki/Anisotropy#Physics
-
Cosmic background radiation spectral radiance peak frequencies...
...
-
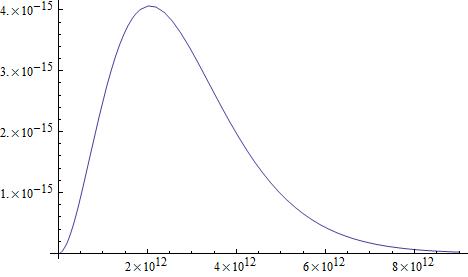
Cosmic background radiation spectral radiance peak frequencies...
\[\color{blue}{\text{Symbolic identity key:}}\] \[\begin{array}{lcl} \text{s} \text{ - spin quantum number} \\ n_{s} \text{ - spin states total integer helicity number} \\ N_{s} \text{ - species total integer number} \\ N_{n} \text{ - total effective degeneracy number} \\ \end{array}\] \[n_{s} = 2 s + 1 \; \; \; \; \; \; s < 2 \; \; \; \; \; \; m = 0\] \[n_{s} = 2 \; \; \; \; \; \; s \geq 2 \; \; \; \; \; \; m = 0\] \[\text{if } n_{s} \geq N_{s} \text{ then } N_{n} = n_{s}\] \[\text{if } n_{s} \leq N_{s} \text{ then } N_{n} = N_{s}\] \[\color{blue}{\text{Toy model quantum particle properties chart:}}\] \[\begin{array}{l*{9}{c}r} & \text{identity} & \text{helicity state} & \text{spin} & n_{s} & N_{s} & N_{n} & \text{mass} & \text{type} & \text{spectral radiance peak frequency} \\ b & \text{quinton} & 0 & 0 & 1 & 1 & 1 & 0 & \Lambda & 2.058 \; \text{THz} \\ b & \text{scalaron} & 0 & 0 & 1 & 1 & 1 & 18.658 \; \text{eV} & \phi & 114.366 \; \text{GHz} \\ f & \text{sterile neutrino} & +,- & 1/2 & 2 & 3 & 3 & 8.167 \; \text{eV} & \nu_{s} & 126.915 \; \text{GHz} \\ f & \text{neutrino} & +,- & 1/2 & 2 & 3 & 3 & 0.038 \; \text{eV} & \nu & 126.915 \; \text{GHz} \\ b & \text{photon} & +,- & 1 & 2 & 1 & 2 & 0 & \gamma & 160.229 \; \text{GHz} \\ b & \text{graviton} & +,- & 2 & 2 & 1 & 2 & 0 & \text{G} & 114.366 \; \text{GHz} \\ \end{array}\] \[\color{blue}{\text{For massless quantum particles, the transverse modes cannot exist due to Lorentz invariance.}}\] \[\color{blue}{\text{Only positive and negative helicity states remain. For massless scalar particles, only zero helicity states remain.}}\] \[\color{blue}{\text{The spin 1 photon is also restricted to its positive and negative helicity states, and has a total effective degeneracy number of 2.}}\] \[\color{blue}{\text{A massless graviton has only 2 helicity states, and has a total effective degeneracy number of 2.}}\] \[\color{blue}{\text{Dark energy quinton total effective degeneracy number:}}\] \[\boxed{N_{\Lambda} = 1}\] \[\color{blue}{\text{Planck satellite dark energy cosmological composition parameter:} \; (\text{ref. 1, pg. 11})}\] \[\Omega_{\Lambda} = 0.6825\] \[\color{blue}{\text{Bose-Einstein dark energy cosmic quinton background radiation temperature:} \; (\text{ref. 2})}\] \[\boxed{T_{\Lambda} = \frac{}{k_{B}} \left(\frac{45 \Omega_{\Lambda} H_0^2 \hbar^3 c^5}{4 G N_{\Lambda} \pi^3} \right)^{1/4}}\] \[\boxed{T_{\Lambda} = 35.013 \; \text{K}}\] \[\color{blue}{\text{Bose-Einstein dark energy cosmic quinton background radiation spectral radiance peak frequency:}}\] \[\boxed{f_{\Lambda} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{\Lambda}}{h}}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\boxed{f_{\Lambda} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right]}{2 \pi} \left(\frac{45 \Omega_{\Lambda} H_0^2 c^5}{4 \hbar G N_{\Lambda} \pi^3} \right)^{1/4}}\] \[\boxed{f_{\Lambda} = 2.05837 \cdot 10^{12} \; \text{Hz}}\] \[\boxed{f_{\Lambda} = 2.058 \; \text{THz}}\] \[\color{blue}{\text{Cosmic photon background radiation temperature at present time:} \; (\text{ref. 4})}\] \[T_{\gamma} = 2.72548 \; \text{K}\] \[\color{blue}{\text{Cosmic neutrino and sterile neutrino background radiation temperature at present time:} \; (\text{ref. 5})}\] \[T_{\nu} = \left(\frac{4}{11} \right)^{\frac{1}{3}} T_{\gamma} = 1.945 \; \text{K}\] \[\boxed{T_{\nu} = 1.945 \; \text{K}}\] \[\color{blue}{\text{Dark matter scalaron and sterile neutrino radiation temperature is equivalent to cosmic neutrino background radiation temperature:}}\] \[\boxed{T_{\phi} = T_{s \nu} = T_{\nu} = 1.945 \; \text{K}}\] \[\color{blue}{\text{Bose-Einstein dark matter cosmic scalaron background radiation spectral radiance peak frequency:}}\] \[\boxed{f_{\phi} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{\phi}}{h}}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\boxed{f_{\phi} = 1.14366 \cdot 10^{11} \; \text{Hz}}\] \[\boxed{f_{\phi} = 114.366 \; \text{GHz}}\] \[\color{blue}{\text{Fermi-Dirac dark matter sterile neutrino background radiation spectral radiance peak frequency:}}\] \[\boxed{f_{s \nu} = \frac{\left[W_{0}\left(\frac{3}{e^3} \right) + 3 \right] k_B T_{\nu}}{h}}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\boxed{f_{s \nu} = 1.26915 \cdot 10^{11} \; \text{Hz}}\] \[\boxed{f_{s \nu} = 126.915 \; \text{GHz}}\] \[\color{blue}{\text{Solve for cosmic neutrino background radiation spectral radiance peak frequency:}}\] \[\color{blue}{\text{Neutrino species total effective degeneracy number:}}\] \[N_{\nu} = 3.046\] \[\color{blue}{\text{Neutrino radiation energy density Fermi-Dirac distribution:}}\] \[\epsilon_{\nu} = \frac{4 \pi N_{\nu} \left(k_B T_{\nu} \right)^4}{\left(2 \pi \hbar c \right)^3} \int_{0}^c \frac{E_t \left(v \right)^3}{e^{\frac{E_t \left(v \right)}{E_1 \left(T_{\nu} \right)}} + 1} dv\] \[\color{blue}{\text{Solve Fermi-Dirac distribution first derivative x-axis zero intercept with respect to frequency:}}\] \[\frac{d \epsilon_{\nu}}{df_{\nu}} = \frac{d}{df_{\nu}} \left(\frac{4 \pi N_{\nu} \left(k_B T_{\nu} \right)^4 E_t\left(\omega \right)^3}{\left(2 \pi \hbar c \right)^3 \left(e^{\frac{E_t \left(\omega \right)}{E_1 \left(T_{\nu} \right)}} + 1 \right)} \right) = 0\] \[\frac{d}{df_{\nu}} \left(\frac{4 \pi N_{\nu} \left(k_B T_{\nu} \right)^4 \left(h f_{\nu} \right)^3 }{\left(h c \right)^3 \left(e^{\frac{h f}{k_{B} T_{\nu}}} + 1 \right)} \right) = \frac{12 \pi N_{\nu} f_{\nu}^2 \left(k_B T_{\nu} \right)^4}{c^3 \left(e^{\frac{h f_{\nu}}{k_B T_{\nu}}} + 1 \right)} - \frac{4 \pi h N_{\nu} f_{\nu}^3 \left(k_B T_{\nu} \right)^3 e^{\frac{h f_{\nu}}{k_B T_{\nu}}}}{c^3 \left(e^{\frac{h f_{\nu}}{k_B T_{\nu}}} + 1 \right)^2} = 0\] \[\frac{12 \pi N_{\nu} f_{\nu}^2 \left(k_B T_{\nu} \right)^4}{c^3 \left(e^{\frac{h f_{\nu}}{k_B T_{\nu}}} + 1 \right)} = \frac{4 \pi h N_{\nu} f_{\nu}^3 \left(k_B T_{\nu} \right)^3 e^{\frac{h f_{\nu}}{k_B T_{\nu}}}}{c^3 \left(e^{\frac{h f_{\nu}}{k_B T_{\nu}}} + 1 \right)^2}\] \[\frac{h f_{\nu}}{k_B T_{\nu}} = 3 \left(1 + \frac{1}{e^{\frac{h f_{\nu}}{k_B T_{\nu}}}} \right) \; \; \; \; \; \; \frac{h f_{\nu}}{k_B T_{\nu}} = 3 + \frac{3}{e^{\frac{h f_{\nu}}{k_B T_{\nu}}}} \; \; \; \; \; \; \frac{h f_{\nu}}{k_B T_{\nu}} = \frac{3}{e^{\frac{h f_{\nu}}{k_B T_{\nu}}}} + 3\] \[\pm x = \left(y \pm a \right) e^{y} \; \; \; \; \; \; y = \frac{x}{e^{y}} + a \; \; \; \; \; \; y = W_{k}\left(\frac{x}{e^{a}} \right) + a \; \; \; \; \; \; x = 3 \; \; \; a = 3 \; \; \; k = 0\] \[f_{\nu} = \frac{\left[W_{0}\left(\frac{3}{e^3} \right) + 3 \right] k_B T_{\nu}}{h} = 1.26915 \cdot 10^{11} \; \text{Hz} = 126.915 \; \text{GHz}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\color{blue}{\text{Fermi-Dirac cosmic neutrino background radiation spectral radiance peak frequency:}}\] \[\boxed{f_{\nu} = \frac{\left[W_{0}\left(\frac{3}{e^3} \right) + 3 \right] k_B T_{\nu}}{h}}\] \[\boxed{f_{\nu} = 1.26915 \cdot 10^{11} \; \text{Hz}}\] \[\boxed{f_{\nu} = 126.915 \; \text{GHz}}\] \[\color{blue}{\text{Solve for cosmic photon background radiation spectral radiance peak frequency:}}\] \[\color{blue}{\text{Photon species total effective degeneracy number:}}\] \[\boxed{N_{\gamma} = 2}\] \[\color{blue}{\text{Cosmic photon background radiation temperature at present time:} \; (\text{ref. 4})}\] \[T_{\gamma} = 2.72548 \; \text{K}\] \[\color{blue}{\text{Planck's law:} \; (\text{ref. 6})}\] \[B\left(f_{\gamma},T_{\gamma} \right) = \frac{N_{\gamma} h f_{\gamma}^{3}}{c^{2} \left(e^{\frac{h f_{\gamma}}{k_{B} T_{\gamma}}} - 1 \right)}\] \[\color{blue}{\text{Solve Bose-Einstein Planck's law first derivative x-axis zero intercept with respect to frequency:}}\] \[\frac{dB\left(f_{\gamma},T_{\gamma} \right)}{df_{\gamma}} = \frac{d}{df_{\gamma}} \left[\frac{N_{\gamma} h f_{\gamma}^{3}}{c^{2} \left(e^{\frac{h f_{\gamma}}{k_{B} T_{\gamma}}} - 1 \right)} \right] = 0\] \[\color{blue}{\text{Planck's law first derivative with respect to frequency:}}\] \[\frac{dB\left(f_{\gamma},T_{\gamma} \right)}{df_{\gamma}} = \frac{d}{df_{\gamma}} \left[\frac{N_{\gamma} h f_{\gamma}^{3}}{c^{2} \left(e^{\frac{h f_{\gamma}}{k_{B} T_{\gamma}}} - 1 \right)} \right] = \frac{3 N_{\gamma} h f_{\gamma}^2}{c^2 \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)} - \frac{N_{\gamma} h^2 f_{\gamma}^3 e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}}{c^2 k_B T_{\gamma} \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)^2} = 0\] \[\frac{3 N_{\gamma} h f_{\gamma}^2}{c^2 \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)} = \frac{N_{\gamma} h^2 f_{\gamma}^3 e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}}{c^2 k_B T_{\gamma} \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)^2}\] \[\frac{h f_{\gamma}}{k_B T_{\gamma}} = 3 \left(1 - \frac{1}{e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}} \right) \; \; \; \; \; \; \frac{h f_{\gamma}}{k_B T_{\gamma}} = 3 - \frac{3}{e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}} \; \; \; \; \; \; \frac{h f_{\gamma}}{k_B T_{\gamma}} = -\frac{3}{e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}} + 3\] \[\pm x = \left(y \pm a \right) e^{y} \; \; \; \; \; \; y = -\frac{x}{e^{y}} + a \; \; \; \; \; \; y = W_{k}\left(-\frac{x}{e^{a}} \right) + a \; \; \; \; \; \; x = -3 \; \; \; a = 3 \; \; \; k = 0\] \[f_{\gamma} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{\gamma}}{h} = 1.60229 \cdot 10^{11} \; \text{Hz} = 160.229 \; \text{GHz}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\color{blue}{\text{Bose-Einstein cosmic photon background radiation spectral radiance peak frequency:}}\] \[\boxed{f_{\gamma} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{\gamma}}{h}}\] \[\boxed{f_{\gamma} = 1.60229 \cdot 10^{11} \; \text{Hz}}\] \[\boxed{f_{\gamma} = 160.229 \; \text{GHz}}\] \[\color{blue}{\text{Observed cosmic photon background radiation spectral radiance peak frequency:} \; (\text{ref. 4})}\] \[f_{\gamma} = 160.23 \; \text{GHz}\] \[\color{blue}{\text{Solve for cosmic photon background radiation spectral radiance peak frequency:}}\] \[\color{blue}{\text{Photon radiation energy density Bose-Einstein distribution:}}\] \[\epsilon_{\gamma} = \frac{4 \pi N_{\gamma} \left(k_B T_{\gamma} \right)^4}{\left( 2 \pi \hbar c \right)^3} \int_{0}^\infty \frac{E_t \left(\omega \right)^3}{e^{\frac{E_t \left(\omega \right)}{E_1 \left(T_{\gamma} \right)}} - 1} d \omega\] \[\color{blue}{\text{Solve Bose-Einstein distribution first derivative x-axis zero intercept with respect to frequency:}}\] \[\frac{d \epsilon_{\gamma}}{df_{\gamma}} = \frac{d}{df_{\gamma}} \left(\frac{4 \pi N_{\gamma} \left(k_B T_{\gamma} \right)^4 E_t\left(\omega \right)^3}{\left(2 \pi \hbar c \right)^3 \left(e^{\frac{E_t \left(\omega \right)}{E_1 \left(T_{\gamma} \right)}} - 1 \right)} \right) = 0\] \[\frac{d}{df_{\gamma}} \left(\frac{4 \pi N_{\gamma} \left(k_B T_{\gamma} \right)^4 \left(h f_{\gamma} \right)^3 }{\left(h c \right)^3 \left(e^{\frac{h f}{k_{B} T_{\gamma}}} - 1 \right)} \right) = \frac{12 \pi N_{\gamma} f_{\gamma}^2 \left(k_B T_{\gamma} \right)^4}{c^3 \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)} - \frac{4 \pi h N_{\gamma} f_{\gamma}^3 \left(k_B T_{\gamma} \right)^3 e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}}{c^3 \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)^2} = 0\] \[\frac{12 \pi N_{\gamma} f_{\gamma}^2 \left(k_B T_{\gamma} \right)^4}{c^3 \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)} = \frac{4 \pi h N_{\gamma} f_{\gamma}^3 \left(k_B T_{\gamma} \right)^3 e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}}{c^3 \left(e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}} - 1 \right)^2}\] \[\frac{h f_{\gamma}}{k_B T_{\gamma}} = 3 \left(1 - \frac{1}{e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}} \right) \; \; \; \; \; \; \frac{h f_{\gamma}}{k_B T_{\gamma}} = 3 - \frac{3}{e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}} \; \; \; \; \; \; \frac{h f_{\gamma}}{k_B T_{\gamma}} = -\frac{3}{e^{\frac{h f_{\gamma}}{k_B T_{\gamma}}}} + 3\] \[\pm x = \left(y \pm a \right) e^{y} \; \; \; \; \; \; y = -\frac{x}{e^{y}} + a \; \; \; \; \; \; y = W_{k}\left(-\frac{x}{e^{a}} \right) + a \; \; \; \; \; \; x = -3 \; \; \; a = 3 \; \; \; k = 0\] \[f_{\gamma} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{\gamma}}{h} = 1.60229 \cdot 10^{11} \; \text{Hz} = 160.229 \; \text{GHz}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\color{blue}{\text{Bose-Einstein cosmic photon background radiation spectral radiance peak frequency:}}\] \[\boxed{f_{\gamma} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{\gamma}}{h}}\] \[\boxed{f_{\gamma} = 1.60229 \cdot 10^{11} \; \text{Hz}}\] \[\boxed{f_{\gamma} = 160.229 \; \text{GHz}}\] \[\color{blue}{\text{Observed cosmic photon background radiation spectral radiance peak frequency:} \; (\text{ref. 4})}\] \[f_{\gamma} = 160.23 \; \text{GHz}\] \[\color{blue}{\text{Cosmic graviton background radiation temperature is equivalent to cosmic neutrino background radiation temperature:}}\] \[\boxed{T_{G} = T_{\nu} = 1.945 \; \text{K}}\] \[\color{blue}{\text{Bose-Einstein cosmic graviton background radiation spectral radiance peak frequency:}}\] \[\boxed{f_{G} = \frac{\left[W_{0}\left(-\frac{3}{e^3} \right) + 3 \right] k_B T_{G}}{h}}\] \[W_{0}\left(z \right) - \text{Lambert W function} \; \left(\text{ref. 3} \right)\] \[\boxed{f_{G} = 1.14366 \cdot 10^{11} \; \text{Hz}}\] \[\boxed{f_{G} = 114.366 \; \text{GHz}}\] \[\color{blue}{\text{Are Fermilab quantum particle detectors capable of detecting cold dark matter quantum particles?} \; (\text{ref. 7})}\] \[\color{blue}{\text{Any discussions and/or peer reviews about this specific topic thread?}}\] Reference: Planck 2013 results. XVI. Cosmological parameters: (ref. 1) http://www.ymambrini.com/My_World/Articles_files/Planck_2013_results_16.pdf Science Forums - Dark energy quinton radiation temperature - Orion1: (ref. 2) https://www.scienceforums.net/topic/86694-observable-universe-mass/?do=findComment&comment=931225 Wikipedia - Lambert W function: (ref. 3) https://en.wikipedia.org/wiki/Lambert_W_function Wikipedia - Cosmic microwave background - Importance of precise measurement: (ref. 4) https://en.wikipedia.org/wiki/Cosmic_microwave_background#Importance_of_precise_measurement Wikipedia - Cosmic neutrino background - Derivation of the CvB temperature: (ref. 5) https://en.wikipedia.org/wiki/Cosmic_neutrino_background#Derivation_of_the_CνB_temperature Wikipedia - Planck's law: (ref. 6) https://en.wikipedia.org/wiki/Planck's_law Fermilab - How scientists at Fermilab search for dark matter particles: (ref. 7) https://bit.ly/3AvGTo9 Science Forums - Toy model calculation versus observation comparison summary - Orion1: (ref. 8 ) https://www.scienceforums.net/topic/86694-observable-universe-mass/?do=findComment&comment=1112539
- Testing latex
-
Testing latex
y=∫f(x)dx Thanks joigus! \[ \color{blue}{\text{test}} \]
-
Testing latex
@joigus, how did you center your equations? I cannot get \begin{center} command to work.
- Testing latex
-
Testing latex
[math]\begin{align} \text{text} \end{align}[/math] [math]\color{blue}{\text{text}}[/math] text [math]F = ma[/math]
-
test
- Astrophysicists unveil biggest-ever 3D map of Universe...
Affirmative. I have located the official "Extended Baryon Oscillation Spectroscopic Survey (eBOSS)" website, listed in reference. The eBOSS team is using a universal time coordinate scale as the domain axis on their map, however, I am also interested in examining the CMBR photon surface of last scattering radial metric distance used on this map, the metric correspondence between space and time, called space-time. If anyone is able to cite a reference to that eBOSS CMBR radial metric data, please post a reference link. This is the YouTube "visualization of the data" video linked from their website: Reference: The Extended Baryon Oscillation Spectroscopic Survey (eBOSS) website: https://www.sdss.org/surveys/eboss/ The full list of publications from eBOSS: https://ui.adsabs.harvard.edu/public-libraries/zjBkevkvQoCBUhWbnd38qg- Astrophysicists unveil biggest-ever 3D map of Universe...
Astrophysicists unveil biggest-ever 3D map of Universe: The map is very isotropic and homogeneous, the large scale galactic filaments are not as apparent on this scale. Discussion? Isotropic: .(of an object or substance) having a physical property which has the same value when measured in different directions. .(of a property or phenomenon) not varying in magnitude according to the direction of measurement. Homogeneous: .of uniform structure or composition throughout. Reference: https://www.ctvnews.ca/sci-tech/astrophysicists-unveil-biggest-ever-3d-map-of-universe-1.5030682- The Lagrangian equation...
Affirmative, revision complete. Relativistic Lagrangian: [math]\boxed{\mathcal{L} = \sum_{1}^{n} \mathcal{L}\left(n \right) = 0} \; \; \; n = 5[/math] [math]\;[/math] Lagrangian equation for a massless quantum field: [math]\; \; \; m = 0[/math] [math]\mathcal{L} = \underbrace{ \mathbb{R} }_{\text{GR}} - \overbrace{\underbrace{\frac{1}{4} F^{\mu \nu} F_{\mu \nu}}_{\text{Yang-Mills}}}^{\text{Maxwell}} + \underbrace{i \overline{\psi} \gamma^\mu D_{\mu} \psi}_{\text{Dirac}} + \underbrace{|D_{\mu} \phi|^{2} - V\left(|\phi| \right)}_{\text{Higgs}} - \underbrace{g \overline{\psi} \psi}_{\text{Yukawa}} = 0[/math] [math]\;[/math] Lagrangian equation for a massless quantum field: [math]\; \; \; m = 0[/math] [math]\boxed{\mathcal{L} = \overbrace{\underbrace{\Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} M^{\alpha \beta}\left(x \right) }_{\text{Quantum Gravity}}}^{\text{spin } 2} - \overbrace{\underbrace{\frac{1}{4} F^{a \mu \nu} F^{a}_{\mu \nu}}_{\text{Yang-Mills}}}^{\text{spin } 1} + \overbrace{\underbrace{i \overline{\psi}_{a} \gamma^{\mu}_{ab} D_{\mu} \psi_{b}}}_{\text{Dirac}}^{\text{spin } 1/2} + \overbrace{\underbrace{|D_{\mu} \phi_{a}|^{2} - V\left(|\phi_{a}| \right)}}_{\text{Higgs}}^{\text{spin } 0} - \overbrace{\underbrace{g \overline{\psi}_{a} \psi_{b}}}_{\text{Yukawa}}^{\text{spin } 0,1/2} = 0}[/math] (ref. 1, ref. 2, ref. 3, ref. 4, ref. 5, ref. 6, ref. 7) [math]\;[/math] Lagrangian equation for a mass quantum field: [math]\; \; \; m \neq 0[/math] [math]\boxed{\mathcal{L} = \overbrace{\underbrace{\Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} M^{\alpha \beta}\left(x \right) }_{\text{Quantum Gravity}}}^{\text{spin } 2} - \overbrace{\underbrace{\frac{1}{4} F^{a \mu \nu} F^{a}_{\mu \nu}}_{\text{Yang-Mills}}}^{\text{spin } 1} + \overbrace{\underbrace{\overline{\psi}_{a} \left(i \gamma^{\mu}_{ab} D_{\mu} - m \mathbb{I}_{ab} \right) \psi_{b}}}_{\text{Dirac}}^{\text{spin } 1/2} + \overbrace{\underbrace{|D_{\mu} \phi_{a}|^{2} - V\left(|\phi_{a}| \right)}}_{\text{Higgs}}^{\text{spin } 0} - \overbrace{\underbrace{g \overline{\psi}_{a} \psi_{b}}}_{\text{Yukawa}}^{\text{spin } 0,1/2} = 0}[/math] (ref. 4, ref. 5) [math]\;[/math] Lagrangian equation for a mass and charge quantum field: [math]\; \; \; m \neq 0, Q \neq 0[/math] [math]\boxed{\mathcal{L} = \overbrace{\underbrace{\Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} M^{\alpha \beta}\left(x \right) }_{\text{Quantum Gravity}}}^{\text{spin } 2} - \overbrace{\underbrace{\frac{1}{4} F^{a \mu \nu} F^{a}_{\mu \nu}}_{\text{Yang-Mills}}}^{\text{spin } 1} + \overbrace{\underbrace{\overline{\psi}_{a} \left[\gamma^{\mu}_{ab} \left(i \partial_{\mu} - e Q A_{\mu} \right) - m \mathbb{I}_{ab} \right] \psi_{b}}}_{\text{Dirac}}^{\text{spin } 1/2} + \overbrace{\underbrace{|\left(\partial_{\mu} -ieQA_{\mu} \right) \phi_{a}|^{2} - \lambda \left(|\phi_{a}|^{2} - \Phi^{2} \right)^{2}}}_{\text{Higgs}}^{\text{spin } 0,1} - \overbrace{\underbrace{g \overline{\psi}_{a} \psi_{b}}}_{\text{Yukawa}}^{\text{spin } 0,1/2} = 0}[/math] (ref. 4, pg. 8, eq. 2.6, ref. 5, ref. 6, ref. 7) [math]\;[/math] Is this approach mathematically and symbolically correct to this point? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Quantum gravity: (ref. 1) https://en.wikipedia.org/wiki/Quantum_gravity Science Forums - Orion1 - Spin 2 Quantum Gravity: (ref. 2) https://www.scienceforums.net/topic/117992-the-lagrangian-equation/?do=findComment&comment=1128193 Wikipedia - Yang–Mills theory: (ref. 3) https://en.wikipedia.org/wiki/Yang–Mills_theory#Mathematical_overview Search For The Standard Model Higgs Boson - Huong Thi Nguyen: (ref. 4) https://www-d0.fnal.gov/results/publications_talks/thesis/nguyen/thesis.pdf Wikipedia - Dirac fields: (ref. 5) https://en.wikipedia.org/wiki/Fermionic_field#Dirac_fields Wikipedia - Higgs mechanism: (ref. 6) https://en.wikipedia.org/wiki/Higgs_mechanism#Abelian_Higgs_mechanism Wikipedia - Yukawa interaction: (ref. 7) https://en.wikipedia.org/wiki/Yukawa_interaction#The_action- The Lagrangian equation...
Affirmative, revision complete. First order metric tensor field for spin-0 and spin-1 particles: (ref. 1, pg. 21, eq. 1.68) [math]T^{'\mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] Second order metric tensor field for spin-2 particles: (ref. 3) [math]M^{'\mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} M^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] The graviton is a spin-two particle, as opposed to the spin-one photon, so that the interaction forms are somewhat more complex, involving symmetric and traceless second order tensors rather than simple Lorentz four-vectors. [math]\;[/math] In relativistic mechanics, the Center Of Mass-Energy boost and orbital 3-space angular momentum of a rotating object are combined into a four-dimensional bivector in terms of the four-position X and the four-momentum P of the object. (ref. 3) [math]\mathbf{M} = \mathbf{X} \wedge \mathbf{P}[/math] [math]\;[/math] With matrix components: [math]M^{\alpha \beta} = X^{\alpha} P^{\beta} - X^{\beta} P^{\alpha}[/math] [math]\;[/math] Which are six independent quantities altogether. Since the components of X and P are frame-dependent, so is M. Three components [math]M^{ij} = x^{i} p^{j} - x^{j} p^{i} = L^{ij}[/math] [math]\;[/math] are those of the familiar classical 3-space orbital angular momentum, and the other three components [math]M^{0i} = x^{0} p^{i} - x^{i} p^{0} = c \; \left(tp^{i} - x^{i}{\frac{E}{c^{2}}} \right) = -cN^{i}[/math] are the relativistic mass moment, multiplied by -c. The tensor is antisymmetric: [math]M^{\alpha \beta} = -M^{\beta \alpha}[/math] [math]\;[/math] The components of the tensor can be systematically displayed as a matrix. [math]\;[/math] The angular momentum [math]L = x \; \wedge \; p[/math] of a particle with relativistic mass m and relativistic momentum p, as measured by an observer in a lab frame, combines with another vector quantity dynamic mass-energy moment [math]N = mx - pt[/math] in the relativistic angular momentum tensor: (ref. 2) [math]M^{\alpha \beta} = {\begin{pmatrix} 0 & -N_{x}^{1}c & -N_{y}^{2}c & -N_{z}^{3}c \\ N_{x}^{1}c & 0 & L^{12} & -L^{13} \\ N_{y}^{2}c & -L^{21} & 0 & L^{23} \\ N_{z}^{3}c & L^{31} & -L^{32} & 0 \end{pmatrix}}[/math] [math]\;[/math] In classical mechanics, the orbital angular momentum of a particle with instantaneous three-dimensional position vector [math]x = (x, y, z)[/math] and momentum vector [math]p = (px, py, pz)[/math], is defined as the axial vector: (ref. 4) [math]\mathbf{L} = \mathbf{x} \times \mathbf{p}[/math] [math]\;[/math] Which has three components, that are systematically given by cyclic permutations of Cartesian directions, change x to y, y to z, z to x, repeat. [math]L_{x} = yp_{z} - zp_{y}[/math] [math]L_{y} = zp_{x} - xp_{z}[/math] [math]L_{z} = xp_{y} - yp_{x}[/math] [math]\;[/math] A related definition is to conceive orbital angular momentum as a plane element. This can be achieved by replacing the cross product by the exterior product in the language of exterior algebra, and angular momentum becomes a contravariant second order antisymmetric tensor: [math]\mathbf{L} = \mathbf{x} \wedge \mathbf{p}[/math] [math]\;[/math] or writing [math]x = (x_{1}, x_{2}, x_{3}) = (x, y, z)[/math] and momentum vector [math]p = (p_{1}, p_{2}, p_{3}) = (p_{x}, p_{y}, p_{z})[/math], the components can be compactly abbreviated in tensor index notation: [math]L^{ij} = x^{i} p^{j} - x^{j} p^{i}[/math] [math]\;[/math] Where the indices i and j take the values 1, 2, 3. On the other hand, the components can be systematically displayed fully in a 3 x 3 antisymmetric matrix: [math]\mathbf{L} = {\begin{pmatrix} L^{11} & L^{12} & L^{13} \\ L^{21} & L^{22} & L^{23} \\ L^{31} & L^{32} & L^{33} \\ \end{pmatrix}} = {\begin{pmatrix} 0 & L_{xy} & L_{xz} \\ L_{yx} & 0 & L_{yz} \\ L_{zx} & L_{zy} & 0 \end{pmatrix}} = \begin{pmatrix} 0 & L_{xy} & -L_{zx} \\ -L_{xy} & 0 & L_{yz} \\ L_{zx} & -L_{yz} & 0 \end{pmatrix}[/math] [math]\;[/math] [math]\mathbf{L} = {\begin{pmatrix} 0 & xp_{y} - yp_{x} & -\left(zp_{x} - xp_{z} \right) \\ -\left(xp_{y} - yp_{x} \right) & 0 & yp_{z} - zp_{y} \\ zp_{x} - xp_{z} & -\left(yp_{z} - zp_{y} \right) & 0 \end{pmatrix}}[/math] [math]\;[/math] This quantity is additive, and for an isolated system, the total angular momentum of a system is conserved. [math]\;[/math] Dynamic mass-energy moment: [math]\mathbf{N} = m \mathbf{x} - \mathbf{p} t = \frac{E}{c^{2}} \mathbf{x} - \mathbf{p} t = \gamma (\mathbf{u}) m_{0} (\mathbf{x} - \mathbf{u} t)[/math] [math]\;[/math] Expressing N in terms of relativistic mass-energy and momentum, rather than rest mass and velocity, avoids extra Lorentz factors. However, relativistic mass is discouraged by some authors since it can be a misleading quantity to apply in certain equations. [math]\;[/math] Defined here so that the relativistic equation in terms of the relativistic mass-energy equivalence, and classical definition, have the same form. The Cartesian components are: [math]N_{x} = mx - p_{x} t = \frac{E}{c^{2}} x - p_{x} t = \gamma \left(u \right) m_{0}\left(x - u_{x} t \right)[/math] [math]N_{y} = my - p_{y} t = \frac{E}{c^{2}} y - p_{y} t = \gamma \left(u \right) m_{0}\left(y - u_{y} t \right)[/math] [math]N_{z} = mz - p_{z} t = \frac{E}{c^{2}} z - p_{z} t = \gamma \left(u \right) m_{0}\left(z - u_{z} t \right)[/math] [math]\;[/math] For a massless spin-2 graviton, [math]E = pc[/math], and the relativistic angular momentum tensor is: [math]M^{\alpha \beta} = {\begin{pmatrix} 0 & -p_{x}\left(\frac{x}{c} - t \right) & -p_{y}\left(\frac{y}{c} - t \right) & -p_{z}\left(\frac{z}{c} - t \right) \\ p_{x}\left(\frac{x}{c} - t \right) & 0 & xp_{y} - yp_{x} & -\left(zp_{x} - xp_{z} \right) \\ p_{y}\left(\frac{y}{c} - t \right) & -\left(xp_{y} - yp_{x} \right) & 0 & yp_{z} - zp_{y} \\ p_{z}\left(\frac{z}{c} - t \right) & zp_{x} - xp_{z} & -\left(yp_{z} - zp_{y} \right) & 0 \end{pmatrix}}[/math] [math]\;[/math] In spherical coordinates [math](ct, r, \theta, \phi)[/math] the Minkowski flat spacetime metric in contravariant form: [math]ds^{2} = -c^{2} dt^{2} + dr^{2} + r^{2} d\theta^{2} + r^{2} \sin^{2} \theta \; d\phi^{2}[/math] [math]\;[/math] In spherical coordinates [math](ct, r, \theta, \phi)[/math] the relativistic angular momentum tensor in contravariant form: [math]M^{\alpha \beta} = {\begin{pmatrix} 0 & -p_{x}\left(\frac{dr}{c} - t \right) & -p_{y}\left(\frac{r d\phi}{c} - t \right) & -p_{z}\left(\frac{r \sin \theta d\phi}{c} - t \right) \\ p_{x}\left(\frac{dr}{c} - t \right) & 0 & dr p_{y} - r d\theta p_{x} & -\left(r \sin \theta d\phi p_{x} - dr p_{z} \right) \\ p_{y}\left(\frac{r d\theta}{c} - t \right) & -\left(dr p_{y} - r d\theta p_{x} \right) & 0 & r d\theta p_{z} - r \sin \theta d\phi p_{y} \\ p_{z}\left(\frac{r \sin \theta d\phi}{c} - t \right) & r \sin \theta d\phi p_{x} - dr p_{z} & -\left(r d\theta p_{z} - r \sin \theta d\phi p_{y} \right) & 0 \end{pmatrix}}[/math] [math]\;[/math] General Relativity stress-energy tensor: [math]M_{\mu \nu} = \pm \left(\begin{matrix} -\rho\left(r \right) c^{2} & 0 & 0 & 0 \\ 0 & p\left(r \right) & 0 & 0 \\ 0 & 0 & p\left(r \right) & 0 \\ 0 & 0 & 0 & p\left(r \right) \end{matrix} \right)[/math] [math]\;[/math] Jacobian matrix transformation matrices: (ref. 5, pg. 15, eq. 41, para. 1, ref 6) [math]\Lambda^{\mu}_{\alpha} = \frac{\partial \xi^{\mu} }{\partial x^{\alpha}} \; \; \; \; \; \; \Lambda^{\nu}_{\beta} = \frac{\partial \xi^{\nu}}{\partial x^{\beta}}[/math] [math]\;[/math] [math]x^{\alpha} = \left(ct, r, \theta, \phi \right) \; \; \; \; \; \; x^{\beta} = \left(ct, r, \theta, \phi \right)[/math] [math]\;[/math] [math]\Lambda^{\mu}_{\alpha} \left(ct, r, \theta, \phi \right) = {\begin{bmatrix} \dfrac{\partial \xi^0}{c^{2} \partial t^0} & 0 & 0 & 0 \\ 0 & \dfrac{\partial \xi^1}{\partial r^1} & 0 & 0 \\ 0 & 0 & \dfrac{\partial \xi^2}{\partial \theta^2} & 0 \\ 0 & 0 & 0 & \dfrac{\partial \xi^3}{\partial \phi^3} \\ \end{bmatrix}} = {\begin{bmatrix} -2 dt & 0 & 0 & 0 \\ 0 & 2 dr & 0 & 0 \\ 0 & 0 & 2r^2 d\theta & 0 \\ 0 & 0 & 0 & 2r^2 \sin^{2} \theta \; d\phi \\ \end{bmatrix}}[/math] [math]\;[/math] [math]\;[/math] [math]\Lambda^{\nu}_{\beta} \left(ct, r, \theta, \phi \right) = {\begin{bmatrix} \dfrac{\partial \xi^0}{c^{2} \partial t^0} & 0 & 0 & 0 \\ 0 & \dfrac{\partial \xi^1}{\partial r^1} & 0 & 0 \\ 0 & 0 & \dfrac{\partial \xi^2}{\partial \theta^2} & 0 \\ 0 & 0 & 0 & \dfrac{\partial \xi^3}{\partial \phi^3} \\ \end{bmatrix}} = {\begin{bmatrix} -2 dt & 0 & 0 & 0 \\ 0 & 2 dr & 0 & 0 \\ 0 & 0 & 2r^2 d\theta & 0 \\ 0 & 0 & 0 & 2r^2 \sin^{2} \theta \; d\phi \\ \end{bmatrix}}[/math] [math]\;[/math] The matrix dot product transformation matrices in covariant form for each of the two four-momentum components as seen from two reference frames, S and S' prime: [math]\Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} = {\begin{bmatrix} 4 dt dt' & 0 & 0 & 0 \\ 0 & 4 dr dr' & 0 & 0 \\ 0 & 0 & 4r^2 r'^{2} d\theta \; d\theta' & 0 \\ 0 & 0 & 0 & 4r^2 r'^{2} \sin^{2} \theta \sin^{2} \theta' \; d\phi \; d\phi' \\ \end{bmatrix}}[/math] [math]\;[/math] Newton's constant: (ref. 7, pg. 9, eq. 37) [math]\kappa^{2} = 32 \pi G[/math] [math]\;[/math] General relativity weak field limit spacetime metric: (ref. 7, pg. 9, eq. 37) [math]g_{\mu \nu} = \eta_{\mu \nu} + \kappa h_{\mu \nu}[/math] [math]\;[/math] General Relativity weak field limit spacetime metric and Planck quantum gravity identity 6: [math]\boxed{\frac{8 \pi G}{c^{4}} M_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} M^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} \left(\eta^{\mu \nu} - \kappa h^{\mu \nu} \right)\left(\eta_{\mu \nu} + \kappa h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] Tensor matrix solution key: [math]s\left(\mu, \nu, \alpha, \beta \right)[/math] [math]\;[/math] [math]s\left(1, 1, 1, 2 \right):[/math] [math]\boxed{2 \pi G p\left(r \right) = c^{4}\left(dr' dr^{2} p_{y} - dr dr' r d\theta p_{x} \right)}[/math] [math]\;[/math] [math]s\left(2, 2, 2, 3 \right):[/math] [math]\boxed{2 \pi G p\left(r \right) = c^{4} \left(r^{3} r'^{2} d\theta^{2} d\theta' p_{z} - r^{3} r'^{2} \sin \theta d\theta d\theta' d\phi p_{y} \right)}[/math] [math]\;[/math] With four stress-energy tensor elements and twelve relativistic angular momentum tensor elements, there are forty-eight possible solution keys. [math]\;[/math] Are these energy-momentum tensors compatible with a massless spin-2 graviton? [math]\;[/math] Is this approach mathematically and symbolically correct to this point? [math]\;[/math] Are there any other tensor matrix solution keys that you want to examine? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf Wikipedia - Four-tensor - Second order tensors: (ref. 2) https://en.wikipedia.org/wiki/Four-tensor#Second_order_tensors Wikipedia - Relativistic angular momentum - 4d Angular momentum as a bivector: (ref. 3) https://en.wikipedia.org/wiki/Relativistic_angular_momentum#4d_Angular_momentum_as_a_bivector Wikipedia - Relativistic angular momentum - Orbital 3d angular momentum: (ref. 4) https://en.wikipedia.org/wiki/Relativistic_angular_momentum#Orbital_3d_angular_momentum Introduction to Tensor Calculus for General Relativity - Edmund Bertschinger: (ref. 5) https://web.mit.edu/edbert/GR/gr1.pdf Wikipedia - Jacobian matrix: (ref. 6) https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant#Example_3:_spherical-Cartesian_transformation Barry R. Holstein - Department of Physics-LGRT - University of Massachusetts: (ref. 7) https://arxiv.org/pdf/gr-qc/0607045.pdf- The Lagrangian equation...
Affirmative, revision complete. Metric tensor field: (ref. 1, pg. 21, eq. 1.68) [math]T^{'\mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] In geometry, the line element or length element can be informally thought of as a line segment associated with an infinitesimal displacement vector in a metric space. The length of the line element, which may be thought of as a differential arc length, is a function of the metric tensor. [math]\;[/math] General Relativity line element where spacetime is modelled as a curved Pseudo-Riemannian manifold with an appropriate metric tensor: (ref. 3, ref 4, pg. 15, eq. 41, para. 1) [math]ds^2 = g_{\mu \nu} dx^{\mu} dx^{\nu}[/math] [math]\;[/math] The General Relativity line element with a curved Pseudo-Riemannian manifold metric tensor condition imposes constraints on the coefficients [math]\Lambda^{\mu}_{\nu}[/math] (ref. 3, pg. 1, eq. 3) [math]g_{\mu \nu} = g_{\alpha \beta} \Lambda^{\alpha}_{\mu} \Lambda^{\beta}_{\nu}[/math] [math]\;[/math] General Relativity curved Pseudo-Riemannian manifold line element identity: [math]\boxed{ds^2 = g_{\alpha \beta} \Lambda^{\alpha}_{\mu} \Lambda^{\beta}_{\nu} dx^{\mu} dx^{\nu}}[/math] [math]\;[/math] The [math]g_{\alpha \beta}[/math] metric tensor will vary according to the spacetime being modeled. It can have either or both the covariant and contravariant terms accordingly to the Einstein summation convention. In this form it is specifying covariant. [math]g_{\alpha \beta} = \pm \begin{pmatrix} -\xi^0 & 0 & 0 & 0 \\ 0 & \xi^1 & 0 & 0 \\ 0 & 0 & \xi^2 & 0 \\ 0 & 0 & 0 & \xi^3 \end{pmatrix}[/math] [math]\;[/math] In spherical coordinates [math](ct, r, \theta, \phi)[/math] the Minkowski flat spacetime metric takes the form: [math]ds^{2} = -c^{2} dt^{2} + dr^{2} + r^{2} d\theta^{2} + r^{2} \sin^{2} \theta \; d\phi^{2}[/math] [math]\;[/math] The Minkowski flat spacetime metric in covariant form: [math]ds \; ds' = -c^{2} dt dt' + dr dr' + r r' d\theta \; d\theta' + r r' \sin \theta \sin \theta' \; d\phi \; d\phi'[/math] [math]\;[/math] General relativity stress-energy tensor: [math]T_{\mu \nu} = \pm \left(\begin{matrix} -\rho c^{2} & 0 & 0 & 0 \\ 0 & p & 0 & 0 \\ 0 & 0 & p & 0 \\ 0 & 0 & 0 & p \end{matrix} \right)[/math] [math]\;[/math] General Relativity Minkowski flat spacetime metric tensor in covariant form: [math]T^{\alpha \beta} \left(r \right) = \pm \begin{pmatrix} -c^{2} dt dt' & 0 & 0 & 0 \\ 0 & dr dr' & 0 & 0 \\ 0 & 0 & r r' d\theta \; d\theta' & 0 \\ 0 & 0 & 0 & r r' \sin \theta \sin \theta' \; d\phi \; d\phi' \end{pmatrix}[/math] [math]\;[/math] Jacobian matrix transformation matrices: (ref. 4, ref 5, pg. 15, eq. 41, para. 1) [math]\Lambda^{\mu}_{\alpha} = \frac{\partial \xi^{\mu} }{\partial x^{\alpha}} \; \; \; \; \; \; \Lambda^{\nu}_{\beta} = \frac{\partial \xi^{\nu}}{\partial x^{\beta}}[/math] [math]\;[/math] [math]x^{\alpha} = \left(ct, r, \theta, \phi \right) \; \; \; \; \; \; x^{\beta} = \left(ct, r, \theta, \phi \right)[/math] [math]\;[/math] [math]\Lambda^{\mu}_{\alpha} \left(ct, r, \theta, \phi \right) = {\begin{bmatrix} \dfrac{\partial \xi^0}{c^{2} \partial t^0} & 0 & 0 & 0 \\ 0 & \dfrac{\partial \xi^1}{\partial r^1} & 0 & 0 \\ 0 & 0 & \dfrac{\partial \xi^2}{\partial \theta^2} & 0 \\ 0 & 0 & 0 & \dfrac{\partial \xi^3}{\partial \phi^3} \\ \end{bmatrix}} = {\begin{bmatrix} -2 dt & 0 & 0 & 0 \\ 0 & 2 dr & 0 & 0 \\ 0 & 0 & 2r^2 d\theta & 0 \\ 0 & 0 & 0 & 2r^2 \sin^{2} \theta \; d\phi \\ \end{bmatrix}}[/math] [math]\;[/math] [math]\;[/math] [math]\Lambda^{\nu}_{\beta} \left(ct, r, \theta, \phi \right) = {\begin{bmatrix} \dfrac{\partial \xi^0}{c^{2} \partial t^0} & 0 & 0 & 0 \\ 0 & \dfrac{\partial \xi^1}{\partial r^1} & 0 & 0 \\ 0 & 0 & \dfrac{\partial \xi^2}{\partial \theta^2} & 0 \\ 0 & 0 & 0 & \dfrac{\partial \xi^3}{\partial \phi^3} \\ \end{bmatrix}} = {\begin{bmatrix} -2 dt & 0 & 0 & 0 \\ 0 & 2 dr & 0 & 0 \\ 0 & 0 & 2r^2 d\theta & 0 \\ 0 & 0 & 0 & 2r^2 \sin^{2} \theta \; d\phi \\ \end{bmatrix}}[/math] [math]\;[/math] The matrix dot product transformation matrices in covariant form for each of the two four-momentum components as seen from two reference frames, S and S' prime: [math]\Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} = {\begin{bmatrix} 4 dt dt' & 0 & 0 & 0 \\ 0 & 4 dr dr' & 0 & 0 \\ 0 & 0 & 4r^2 r'^{2} d\theta \; d\theta' & 0 \\ 0 & 0 & 0 & 4r^2 r'^{2} \sin^{2} \theta \sin^{2} \theta' \; d\phi \; d\phi' \\ \end{bmatrix}}[/math] [math]\;[/math] General Relativity weak field limit spacetime metric and Planck quantum gravity identity 4: (ref. 6) [math]\boxed{\frac{8 \pi G}{c^{4}} T_{\mu \nu} = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta} \left(x \right) \left(1 - \frac{1}{2} \left(\eta^{\mu \nu} - h^{\mu \nu} \right)\left(\eta_{\mu \nu} + h_{\mu \nu} \right) \right)}[/math] [math]\;[/math] Solution 1: [math]\mu = \nu = 0[/math] [math]\boxed{2 \pi G \rho \left(r \right) = c^{4} dt^{2} dt'^{2}}[/math] [math]\;[/math] Solution 2: [math]\mu = \nu = 1[/math] [math]\boxed{2 \pi G p \left(r \right) = c^{4} dr^{2} dr'^{2}}[/math] [math]\;[/math] Solution 3: [math]\mu = \nu = 2[/math] [math]\boxed{2 \pi G p \left(r \right) = c^{4} dr^{3} dr'^{3} d\theta^{2} \; d\theta'^{2}}[/math] [math]\;[/math] Solution 4: [math]\mu = \nu = 3[/math] [math]\boxed{2 \pi G p \left(r \right) = c^{4} dr^{3} dr'^{3} \sin^{3} \theta \; \sin^{3} \theta' d\phi^{2} \; d\phi'^{2}}[/math] [math]\;[/math] Is this approach mathematically and symbolically correct to this point? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf Wikipedia - General relativity - Metric tensor - Local coordinates and matrix representations: (ref. 2) https://en.wikipedia.org/wiki/Metric_tensor_(general_relativity)#Local_coordinates_and_matrix_representations Lorentz Transformations - Bernard Durney: (ref. 3) https://arxiv.org/pdf/1103.0156.pdf Introduction to Tensor Calculus for General Relativity - Edmund Bertschinger: (ref. 4) https://web.mit.edu/edbert/GR/gr1.pdf Wikipedia - Jacobian matrix: (ref. 5) https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant#Example_3:_spherical-Cartesian_transformation Science Forums - Lagrangian equation for a massless Planck graviton - Orion1: (ref. 6) https://www.scienceforums.net/topic/117992-the-lagrangian-equation/?do=findComment&comment=1096894- The Lagrangian equation...
Affirmative, revision complete. [math]\eta_{\mu \nu}[/math] - perturbed non-dynamical background metric [math]\;[/math] General Relativity Minkowski flat spacetime metric: (ref. 1) [math]\eta_{\mu \nu} = \pm \begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}[/math] [math]\;[/math] General Relativity Minkowski flat spacetime metric is equivalent to the inverse metric: (ref.1, ref. 2) [math]\boxed{\eta_{\mu \nu} = \eta^{\mu \nu}}[/math] [math]\;[/math] What is the formal mathematical definition for [math]g_{\alpha \beta}[/math]? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Wikipedia - Four-gradient As a Jacobian matrix for the SR Minkowski metric tensor: (ref. 1) https://en.wikipedia.org/wiki/Four-gradient#As_a_Jacobian_matrix_for_the_SR_Minkowski_metric_tensor Wikipeda - Lorentz covariance: (ref. 2) https://en.wikipedia.org/wiki/Lorentz_covariance- The Lagrangian equation...
Affirmative, revision complete. Metric tensor field: (ref. 1, pg. 21, eq. 1.68) [math]T^{'\mu \nu} \left(x' \right) = \Lambda^{\mu}_{\alpha} \Lambda^{\nu}_{\beta} T^{\alpha \beta}\left(x \right)[/math] [math]\;[/math] In geometry, the line element or length element can be informally thought of as a line segment associated with an infinitesimal displacement vector in a metric space. The length of the line element, which may be thought of as a differential arc length, is a function of the metric tensor. [math]\;[/math] General Relativity line element where spacetime is modelled as a curved Pseudo-Riemannian manifold with an appropriate metric tensor: (ref. 3, ref 4, pg. 15, eq. 41, para. 1) [math]ds^2 = g_{\mu \nu} dx^{\mu} dx^{\nu}[/math] [math]\;[/math] The General Relativity line element with a curved Pseudo-Riemannian manifold metric tensor condition imposes constraints on the coefficients [math]\Lambda^{\mu}_{\nu}[/math]: (ref. 3, pg. 1, eq. 3) [math]g_{\mu \nu} = g_{\alpha \beta} \Lambda^{\alpha}_{\mu} \Lambda^{\beta}_{\nu}[/math] [math]\;[/math] General Relativity curved Pseudo-Riemannian manifold line element identity: [math]\boxed{ds^2 = g_{\alpha \beta} \Lambda^{\alpha}_{\mu} \Lambda^{\beta}_{\nu} dx^{\mu} dx^{\nu}}[/math] [math]\;[/math] General Relativity matrix symmetry expression: [math]\mu \cdot \nu = \nu \cdot \mu = \eta[/math] [math]\;[/math] Jacobian matrix transformation matrices: (ref. 4, ref 5, pg. 15, eq. 41, para. 1) [math]\Lambda^{\mu}_{\alpha} = \frac{\partial \xi^{\mu} }{\partial x^{\alpha}} \; \; \; \; \; \; \Lambda^{\nu}_{\beta} = \frac{\partial \xi^{\nu}}{\partial x^{\beta}}[/math] [math]\;[/math] [math]x^{\alpha} = \left(ct, r, \theta, \phi \right) \; \; \; \; \; \; x^{\beta} = \left(ct, r, \theta, \phi \right)[/math] [math]\;[/math] [math]\Lambda^{\mu}_{\alpha} \left(ct, r, \theta, \phi \right) = {\begin{bmatrix} \dfrac{\partial \xi^0}{\partial t^0} & 0 & 0 & 0 \\ 0 & \dfrac{\partial \xi^1}{\partial r^1} & 0 & 0 \\ 0 & 0 & \dfrac{\partial \xi^2}{\partial \theta^2} & 0 \\ 0 & 0 & 0 & \dfrac{\partial \xi^3}{\partial \phi^3} \\ \end{bmatrix}}[/math] [math]\;[/math] [math]\;[/math] [math]\Lambda^{\nu}_{\beta} \left(ct, r, \theta, \phi \right) = {\begin{bmatrix} \dfrac{\partial \xi^0}{\partial t^0} & 0 & 0 & 0 \\ 0 & \dfrac{\partial \xi^1}{\partial r^1} & 0 & 0 \\ 0 & 0 & \dfrac{\partial \xi^2}{\partial \theta^2} & 0 \\ 0 & 0 & 0 & \dfrac{\partial \xi^3}{\partial \phi^3} \\ \end{bmatrix}}[/math] [math]\;[/math] Is this approach mathematically and symbolically correct to this point? [math]\;[/math] What is the formal mathematical definition for [math]g_{\alpha \beta}[/math]? [math]\;[/math] Any discussions and/or peer reviews about this specific topic thread? [math]\;[/math] Reference: Lorentz Group and Lorentz Invariance: (ref. 1) https://gdenittis.files.wordpress.com/2016/04/ayudantiavi.pdf Wikipedia - General relativity - Metric tensor - Local coordinates and matrix representations: (ref. 2) https://en.wikipedia.org/wiki/Metric_tensor_(general_relativity)#Local_coordinates_and_matrix_representations Lorentz Transformations - Bernard Durney: (ref. 3) https://arxiv.org/pdf/1103.0156.pdf Introduction to Tensor Calculus for General Relativity - Edmund Bertschinger: (ref. 4) https://web.mit.edu/edbert/GR/gr1.pdf Wikipedia - Jacobian matrix: (ref. 5) https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant#Example_3:_spherical-Cartesian_transformation - Astrophysicists unveil biggest-ever 3D map of Universe...
Important Information
We have placed cookies on your device to help make this website better. You can adjust your cookie settings, otherwise we'll assume you're okay to continue.