John2020

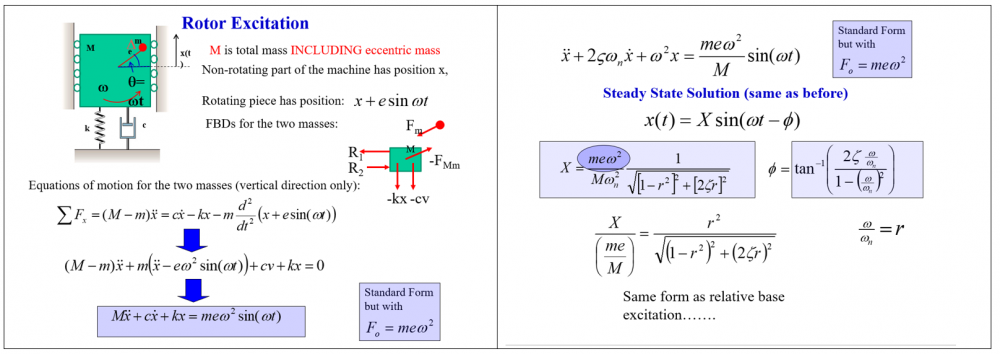
If the mods are planning to close this thread then, please let me know before I start answering the questions of the members placed some hours ago. @swansont, @Ghideon, @exchemist. I hope the below information will help all of you understand what is wrong with your claims (I would say not yours but established claims, a.k.a misconception in the established physics). So we need an experiment and the maths that describe it. According to my view, what is shared below reveals how the ring's motion is justified on a fundamental level (the main cause behind its motion): a) Please could you identify the cause of vibration on the following Eccentric mass setup. Does it require gravity as the cause (means the source) of vibration or not? Note: Please do not confuse the response of the system with the underlying cause, because this is what you are doing the whole time: Eccentric Mass Dynamic Vibrations (watch from 20 sec up to 50 sec -> without the absorber) b) The (a) is described by the following differential equation and particular solution. Could you please identify where gravity is being involved and whether gravity is the cause of vibration? The above answers to all your recent false claims that I do not understand physics and about the system (ring) will not accelerate if there is no g. This is the essence of the entire discussion. If you are of a different opinion, first you need to address the above questions, otherwise this discussion does not need to be continued. c) Assuming you acknowledge the above, there are additional problems to consider: (b) although models the response of the system properly and in absence of gravity, it cannot justify: i) how the momentum is being transferred from the eccentric mass to the rest of the system, ii) violates Newton's 3rd law. When we ever pass (c) which I doubt then, I will reveal the complete expression of Newton's 3rd law. Just for the record, according to my view Newton's 3rd law, covers 2 out of 3 cases and these are: 1) rectilinear motion, 2) circular motion. The missing one is the curvilinear motion which is the one that may justify (b), meaning vibration of an isolated system (since no gravity is being involved. See (b) equations) by means of internal forces.

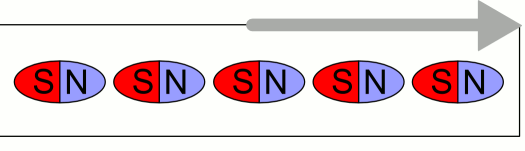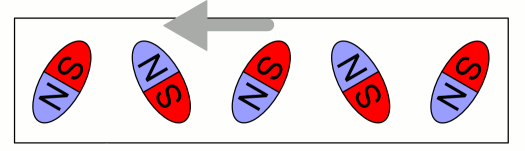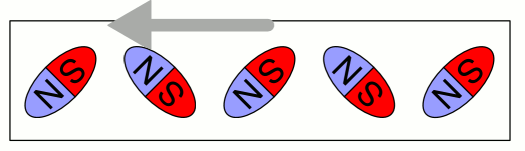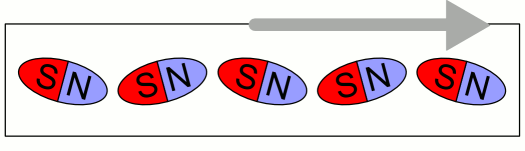
As I said we should pay attention of what we are referred to. Again you are confusing system responses (as that with the car you mention) with the motion of the ring. For once more we have a cycle of 200 μsec and a mass of 200 grams. Thus, a complete cycle means, the magnetic dipole are aligned leftwards and then rightwards. The net force is then zero that means we shouldn't have acceleration. A partial cycle would justify ring's motion Besides you insist of using Gravity to justify the ring's motion, gravity and the normal force (from the table) cannot be the cause of ring's motion, however the normal force plays only a role regarding the static friction that must be overcome in order to start moving. If you pay attention to all three videos the ring has a tendency to rotate which is a fact that a horizontal force is at play and certainly has nothing to do with the normal force. If gravity plays a role then, why it is not part in the differential inhomogeneous equation that describes the rotating unbalance? Moreover, as you may see the particular solution has no reference to a gravitational constant. This is something you still avoid to answer by using excuses that is not the subject in this discussion, however it is physics and related to vibrations. My answer to the erroneous claims about gravity being a necessary ingredient for ring's motion is, please check the differential equation of the rotating unbalance. Exactly as it is the case with the rotating unbalance. See the differential inhomogeneous equation and its particular solution. No g (like zero g) is used, however the equation and the particular solution, describe and conclude the system vibrates. What do you mean, I do not understand? If you mean what is the key of this supposed contradiction between the acknowledge motion and Newton's laws of motion then, the answer is that Newton's 3rd law is incomplete according to my point of view and I can prove it mathematically using a very simple classical mechanics setup. Conclusively, below I have a sequence of statements that may justify ring's motion according to my view: 1) The magnetic field lines running through the ring are in parallel with the table 2) Due to (1) the magnetic dipoles align in the horizontal plane 3) Due to (1) and (2) the forces like gravity and normal force (from the table) in the vertical plane cannot be the cause of its motion (I speak about the cause and not the resulting trajectory (we will speak about this later)) 4) Due to (2) a complete cycle (leftwards and then rightwards alignment) results in no ring's acceleration 5) Due to (4) a partial cycle e.g. π/2, might result in ring's initial acceleration. Important Note: How could that happen? IF we ever continue this discussion, I will explain it. 6) Due to (1) to (5), the acceleration can be attributed only to internal forces (the forced alignment of the magnetic dipoles in the horizontal plane) being responsible for the momentum transfer from the magnetic dipoles to the rest of the system (ring) 7) Due to (6), Newton's laws cannot justify ring's motion from the moment it is not attributed to external forces 8) The reason behind (7) is Newton's 3rd law. Motion by means of internal forces is forbidden because of Newton's 3rd law (as applies for internal forces) therefore, it must be incomplete.

No, because gravity is not part of the solution and this is evident by the horizontal motion in all three videos.

Besides you use the vertical vibration to explain ring's motion that does not make sense, you ignore the fact that within a cycle, the net force is zero that means it should never accelerate. IF and only IF the vibration was developed in just one direction (half-cycle and I speak now for the horizontal plane) then, it would be possible to justify ring's motion in principle. I do not see why the vibration in the vertical plane is a pre-requisite for ring's motion. Note: The magnetic field is in parallel with table surface and the magnetic dipoles align in the horizontal plane. Consequently, ring's motion does not require the "jumping" effect in order to justify its motion.

Yes, in the case of a body but that doesn't mean it has to apply everywhere therefore, I would recommend caution. I suppose, you read my posts above regarding the ring. Let us continue.

I suppose you follow this discussion. So, fast circular change of center of gravity (zero net change in center of gravity) associated with ring's large inertia (200 grams) should result in no motion. It means, besides the net change in center of gravity is zero (after a complete cycle which is relative short, approx. 200 μsec), the ring would be so slow in response that wouldn't even move a millimeter.

I have no evidence about that. If you are associating a probable proof about space anisotropy at small scales with Newton's 3rd law violation, besides I do not see the link between them, it is not required. The proof of Newton's 3rd law incompleteness can be demonstrated and mathematically proven in classical mechanics based on momentum conservation, again and always according to my view. But this is not the current issue in our discussion. We are looking to explain how those experiments comply with Newton's laws of motion. Yes, it can because it has wheels that touch the ground, The wheels act like an action "bridge" between the internal and the external forces. The ring does not have wheels to push the ground although it touches it. In other words, the ring does not expose any moving parts. We are speaking about an oscillation period of 1/5000 Hz = 200 μsec. Due to ring's large inertia, the ring should never move in any direction in any of those three experiments.

Somehow I was expecting such a response after explaining how a person may jump off the ground. It is how things are seen by an external observer, however according to my view, something does not fit the bill. Fig. Magnetostriction As you may see the above .gif animation shows in a way how magnetostriction strain looks like. I am going to develop a couple of arguments but one at a time. Please could you explain: Since the ring is driven by a 5KHz sinus signal and the field changes direction from left to right and vice versa (oscillating) then, after a complete cycle of period T = 1/5KHz wouldn't the contraction/expansion result in a zero net change in the center of gravity?

@exchemistI think I have already addressed how the jump in the air works. OK, let's go one more time step by step: (1) A person contacts its body towards the floor (2) The contraction results in the change of its center of gravity (3) The change (accelerating) of its center of gravity creates a force upon the floor (4) Then the person starts to expands back its body (5) While expanding his body, the center of gravity (accelerating) moves upwards (6) The impulse time (expansion point - contraction point) multiplied by the Force (Action) exerted upon the floor, results in the impulse (divided by the impulse time gives the reaction force from the floor) exerted upon person's body. (7) If this impulse divided by the impulse time is larger than the force of gravity (m*g) then the person will jump off the ground @swansontBecause the windings of the coil (ferrite ring + coil windings = system) is part of the system windings + ring that travel together as a whole. If the winding wasn't wound around the ferrite ring then the magnetic force would be external to the ring.

Again it is not a complicated system in terms of demonstrating the effects. You haven't answered my question regarding the force that comes from inside the ring is internal and then I put another argument that the ring shouldn't vibrate according to Newton's 3rd law and nobody said anything about. Something else is happening or something else obscures the effect according to my view. Therefore, I suggest you to watch the example with the LEGO car, it is clearer (no table vibrations, no gravity influence etc). So, who is in bad faith? In front of experimental evidences that need serious discussion, your only interest is to close the thread because someone presented some logical arguments that do not comply with what you serve (physics). Do whatever you like.

I have explained myself how I put it. If I am wrong, tell me how the LEGO car is moving and what Newton's 3rd law says about it? Gravity and table vibrations have nothing to do with the LEGO car therefore, those claims cannot hold as main cause of motion.

You took it wrong. The simplest system is that with the LEGO car since it does not touch the table and just pushing the car. So, how something may push the car while being inside? What Newton's laws of motion say about it?

About the LEGO car: If you watch closely, you may identify the ring attempts to rotate and while doing that it is blocked by a LEGO piece in front of it. What happens at that moment, the ring seems to push the LEGO piece (being a part of the entire car) that leads to entire LEGO car motion. How Newton's laws may explain this? I cannot find an explanation according to Newton's laws. The only thing I may confirm is the ring attempts to rotate that means a tangential force is at play originated from inside the ring. This can be proven by the Exp #3 with the controllable rotation of the ring. In Exp #3 we may clearly identify the tangential force created by the ring, otherwise the ring wouldn't rotate. Again, there is no interaction with nearby metals or table feet. Note: We speak about a 200 grams ring with high a magnetic permeability (almost all magnetic lines are found inside the ring). See datasheet in my initial posts.

I just make a parallelism regarding the cause of motion. According to Newton's laws of motion, a body or a system may move by means of external forces. According to my understanding regarding the experiments and what we have agreed so far my personal conclusion is that the system moves by means of internal forces as being an isolated system. That is all! This is your point of view and it seems you don't like to confront the issues because you are focused of what I cannot manage, so you think let us take advantage of it and nail him down, right? I don't care. I am not a physicist and I do not claim physics is wrong. On the contrary, I put the material on YouTube and open a thread here in order to discuss it. Each one of us besides knowledge and expertise in our fields, we have some brain and can think in our feet by presenting logical arguments.

The most complicating factors exist on the ring moving across the table which brings much controversy. This is the reason I suggest to check the other two which are clearer as set up and observed effects.