studiot

It's a question of understanding, not doubt. So if I understand you correctly you are taking instance of a quake in England & Wales, without further subdivision, and any occurrence of a riot in the same total area. The UK has a substantially diagonally banded geological structure, running SW to NE. So (and I don't know if the were any), a quake in Deal would be linked to a riot in Barrow-in furness if they fell with your selected time frame. Such a link would cut directly across all those diagonals. I don't know if the other diagonal would be more productive. That is a quake in Penzance linking to another Jarrow riot.

While you mention ground there was a question backalong about the geographic space compared for the riot and the earthquake. Since neither are points in space their choice is enormously important so can you outline how this was done?

Excellent question +1

Hello Alan, I meant to add in tha last post. I hope you take my comments as genuine testing of the methodology, not attempts to discredit the study. The subject is genuinely intriguing.

Another methodology query, Alan. I can be reasonably sure that the BGS report of quakes is accurate. For 'riots' I am less sure about the reporting accuracy. Who reported them to whom Who assessed what the definition of a riot is and whether each report met this definition. How confident can you be that before quake when there may have been little to fill the news space riots were not over reported and after a newsworthy event they were not under-reported.T These factors may not account for the near 3:1 ratio you have presented, but have you considered them? Can I commend to you Standard Deviations by Gary Smith? In particular the discovery of the causes of cholera by methods such as you are employing

Whilst I'm not suprised to hear this, I was more interested in its corollary. There should therefore be a lower than average incidence during periods of inclement weather. You often find freak (inclement) weather associated with/following quake activity. This suggests a pattern (to be investigated) quake [math] \to [/math] freak weather [math] \to [/math] increased/decreased riot activity or perhaps all three can stem from a common cause.

Alan, thank you for sharing this. You seem to have negotiated the proper side of the line in providing enough information in your opening post to justify a link to a much larger paper IMHO. I don't know about the correctness of the hypothesis, I have heard studies of correlations between weather conditions and human (and other life) behaviour and also studies correlating weather conditions with quake activity. So perhaps there are more links to be drawn? An authority who might well be interested is Brian Fagan https://www.google.co.uk/search?q=brian+fagan&hl=en-GB&gbv=2&oq=brian+fagan&gs_l=heirloom-serp.3..0i67j0i7i30l8j0.11781.11781.0.12015.1.1.0.0.0.0.141.141.0j1.1.0....0...1ac.1.34.heirloom-serp..0.1.141.1CHWHcSRVUM

Hello Jenn and welcome. I know nothing of your Saginaw event, and unfortunately our pet geologist who have know escaped nearly a year ago. However I can tell you that meteor impact is associated with what is known as the iridium spike because meteors often contain the very rare (on Earth) element iridium. Googling gives lots of information about more famous impacts and craters, but I haven't found any measurements at your location. Perhaps you should ask your local college or library?

I didn't supply a reference, but the book I drew from is http://www-astro.physics.ox.ac.uk/~pgf/Pedro_Ferreira/The_Perfect_Theory.html Please note this is a great source of understanding and further reading but it is not technical enough for your purposes.

As you know I am a muddy boots, dirty hands technologist. As such I have always felt GR to be inferring too much from too little. So I was suprised to learn that over the years there have been several theories of general relativity, with different terms and constants in the equations changing as new material has arisen. So I recommend you be very aware of which version you incorporate material from.

Well this is the first time I have seen this thread and I am looking forward to reading all the posts carefully. It is a long time since I was motivated to get my boots out of the mud and read detailed thoughts about cosmology. +1 There is much to consider here and the quantity accounts for why we don't see posts from you more often but this caught my eye Several of your bullet points boil down to saying that we can observe effects in the material universe that require another generalised axis, dimension or formalised degree of freedom to explain and write equations for. I agree with this completely and have made this point before, although my example (nuclear disintegration/radioactivity) does not require continuity but relates the phenomena directly to the counting numbers.

Don't forget you entitled this thread curve fitting and interpolation. Pure mathematics only admits one situation and it is deterministic. That is you know the true function and its values at certain data points and want intermediate ones between the points. There is no choice of curve(s) to fit. For example you have sine tables with the sine at every degree and want the sine of 23o 30'. Numerical mathematics adds two more scenarios. Firstly you have a set of data points, but you dont know true function at all. For example you have a set of tide tables with the tide height every 10 minutes and want to correct a set of soundings to mean sea level. You have the soundings at random times in the interval covered by your tables so you need the tide heights at say 11 minutes, 14 minutes, 18 minutes etc. Finally you may know the exact function, but it may be to difficult to handle so you choose a simpler one that is near enough. It is this third method that is the basis of all the finite element computer programs for structural engineering, fluid mechanics, electric and magnetic field plotting and so on. The calculus of variations and Lagrange-Hamiltonian mechanics are ways to choose such simpler functions.

Google the Brachistochrone problem.

Here are a few short thoughts, as it's getting late here. Taught yourself linear algebra. That's something to be proud of and the subject is the basis for many (if not most) of useful mathematics. Tensors take you back into the theoretical arena and a really a part of linear mathematics anyway. Interpolation is definitely in the applied mathematics camp, sub category numerical methods. Note I said numerical methods. There is a much more theoretical subject of numerical analysis. No there is not one (or even a few) grand methods, there are many approaches. We can continue to talk about them if you like, this is a very pleasant thread, much better than those where there is constant arguing for the sake of it. But remember my views are skewed towards the applied side and I make no apology for this. I would say that you would be better advised to look at Hamilton - Lagrange methods and what is called "The Calculus of Variations", rather than pursue tensor methods very deeply. The purpose of the calculus of variations is to determine the best curve through data points according to some pre established criterion. Finite element analysis is when you draw up a (multidimensional) grid or mesh and fit it to whatever you are analysing. You must have seen this in the movies or adverts where a computer 'scans' the hero or a car or something. My avatar picture is a finete element mesh overlaid on a human face. Again we can talk about all this and I will also explain the finite difference table further.

I am very flattered to think that the whole of my rushed explanation was crystal clear since you haven't asked any technical questions, but I'm sure it could be improved. So don't hesitate to ask about what was said. It would be useful at this point to ask what your level of mathematical/technical background is. The second quote sounds like you have seen the finite element grids used in modern analysis of just about everything. Do you know in principle what a diffeential equation is? I am not asking if you know lots of solutions, just if you have the general idea. Then I can give a better answer to the first quote above.

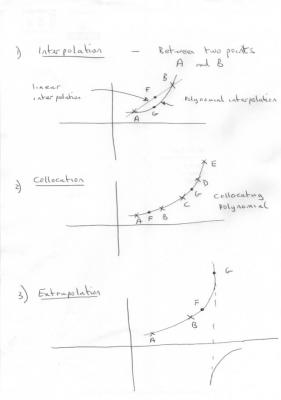
Here is the STRRGI (Studio T Rapid Rough Guide to Interpolation and other itches) Let us say we have a number of data points and wish model this by a curve of known algebraic form, so that we can use the curve to find data at points we do not have the true (or measured) value for. With reference to the figures, I have used large crosses to denote the known data points where it is assumes the values are exact and labelled these points A, B, C, D and E. Points where e want to estimate the value the data would take at these points are labelled F and G in all cases. First comes interpolation. Inter is Latin for between and interpolation is used to estimate the data value between two points. Obviously many different curves can be employed, but we want one that is ‘well behaved’. That is it does not go off to infinity between A and B or execute wiggles etc but in some way moves smoothly and continuously from A to B. I have shown a straight line and a polynomial (probably a quadratic) that have this property. Point F is located on the straight line and Point G on the quadratic, but both have the same x coordinate. So you can see that we already have two different possible estimates for the data value at this x. But we may have a set or table of data values that show a curve, not a straight line. If we model with a polynomial, the curve that passes through (has the same values as the data at ) A, B,C, D and E is called the collocating polynomial. It is said to collocate (be the same as or fit exactly) the data at these points. If we can generate such a polynomial we can have good confidence that points F and G on the curve will be pretty good estimates of the data at their locations. Lastly we come to extrapolation. Extra is Latin for outside and this is where we extend the supposed line beyond the interval bracketed by A and B. In the diagram F is close to B and we can reasonably hope that the estimate that F represents is a good match to the actual data. The further we go the more dicy this assumption becomes. It is a bit like leverage. The longer the lever greater the displacement. This is shown by Point G in the diagram. Point G also shows something else. Your constructed function (don’t worry about my contrived comment it only meant it was an exercise) was a tangent. The tangent goes of to + infinity and then returns from – infinity as shown. So if the data function really does this there is huge scope for error around this point. Now to change the subject entirely. Before the days of calculating machines, tables of mathematical functions were drawn up. Someone had to calculate all these values. How did they do this? You may well ask. Well not by exhaustive computations on series or whatever. That would have been horrific. The method used was the method developed by Newton and which he was playing about with when he developed the Calculus. It is called the method of finite differences, is was a way to obtain data values between entries in a table, from the existing assumed exact ones. The method can be used to obtain any desired level of accuracy if enough exact data points are available. That is the tables can be interpolated to any number of significant figures. Thus it is a method of interpolation and many observed empirical tables such as the international steam tables are still used in this way. Original sine, tangent and logarithmic tables were prepared in this way. As an introduction look at the final diagram which has 5 columns of figures. The first column is a list of the exact data, 1, 8, 27 etc The second column is the difference between successive real data entries so the first one is (8-1 = 7) The third column is the difference between these ‘differences’ So 19 – 7 = 12 The fourth column is the difference between these differences, which you will note are all the same The fifth column is again differences but they are all zero. All subsequent columns would also be zero. If you are observant you will note that the original data is cubic and the columns become constant on the fourth. This is no accident. A quadratic becomes constant on the third etc. So with enough data we can either use these values to reinstate a missing data point in the list, calculate the next one or insert a point partway between two existing ones. Because numerical data tables were once so important a huge body of theory has been developed about the best ways to do this.

Yes I thought it seemed a bit contrived, but I did briefly wonder if there was any relation to the Langevin function.

You can solve for a, b and c because you have exactly the same number of unknowns as equations, so any solution (just have the same number does not guarantee solutions) is exact. If you have more equations than unknowns then, as always, you have redundant information. There are various methods of dealing with this, mostly statistical, which is what I expect you are thinking of. You can assume the form of the fitting equation and calculate a set of auxiliary equations minimising some functions of the deviations that yields a unique set of coefficients. the usual is to minimise the squares of the deviations producing what is known as 'least squares fitting'. We use the squares because they are all positive and thus we can minimise their absolute value. Other statistical methods are available if we want to weight the deviations to remove outliers etc. Another approach entirely may be more appropriate if we are concerned with the slope of the fitting equation at the end points because we can gain some extra equations by differentiating it and fitting the derived curve, at least at the ends. The most popular of this type is are called spline curves. This whole subject is huge. By the way, as a start do you know the difference between interpolation and extrapolation?

You are not trying hard enough. [math]\tan \left\{ {{e^{a{x^2} + bx + c}}} \right\} = 0,\quad at\,x = 0[/math] [math]\tan \left\{ {{e^{ + c}}} \right\} = 0[/math] [math]\tan \left\{ {something} \right\} = 0,\quad something \ne 0[/math] [math]{e^{ + c}} = something[/math] Can you think of something, not equal to zero, that makes tan(something) zero? Hint tan is a periodic function.

You have three unknowns, a, b and c You can obtain three simultaneous equations linking them, by substituting the values for x and y at the known points. You then need to solve the three equations for the coefficients a, b and c. The first one should yield c directly, but think carefully about it, and note that angles will be measured in radians.

Yes I think we are all agreed on this.

Yes so long as you do not try to make injections from the reals to the rationals.

I did wonder at the OP's use of fractions since it implies his underlying set is the set of rational numbers, not the reals. Which is intended needs to be made clear before constructing a proof.

Three hints in the form of questions At what distance travelled does the block reach its final speed? In what direction do we take the velocity be for the purpose of the equations of motion? Velocity is a vector do we need to resolve it in any particular directions?

Welcome +1