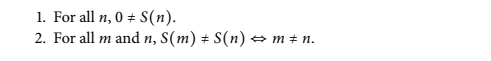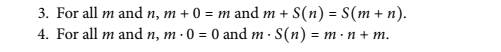Everything posted by Genady
-
"Alien objects", Stillwell's "Reverse Mathematics"
I got the answer - Robinson arithmetic - Wikipedia.
-
Using Grok as a tool.
Yes, the galactic North Pole and our North Pole do not coincide, but this doesn't change the sense of rotation. Important fact is that the galactic North Pole lies in our northern hemisphere. AFAIK, our galaxy rotates clockwise as viewed from the galactic North Pole. This is what I remember from my astronomy class years ago.
-
Using Grok as a tool.
It doesn't sound right. Anyway, here is how it looks:
-
"Alien objects", Stillwell's "Reverse Mathematics"
Stillwell's "Reverse Mathematics" says on p.41, Unfortunately, there is no example of such model. Does anybody know such? For the reference, here are the axioms 1-4:
-
'Are They Dead ?' - Demumu
"Ah, look at all the lonely people"
-
'Are They Dead ?' - Demumu
We have exactly such system where I live. Hospital nurses visit daily elderly living alone.
-
Using Grok as a tool.
Clockwise when observed from the North.
-
Can the universe ever end ?
I thought that Klein-Gordon's describes bosons, while Dirac's describes fermions.
-
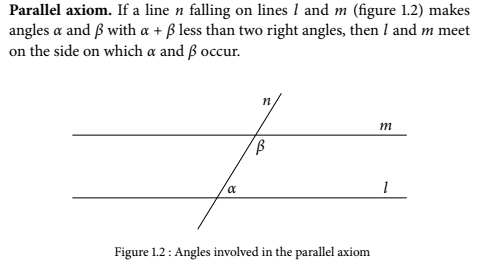
Parallel axiom
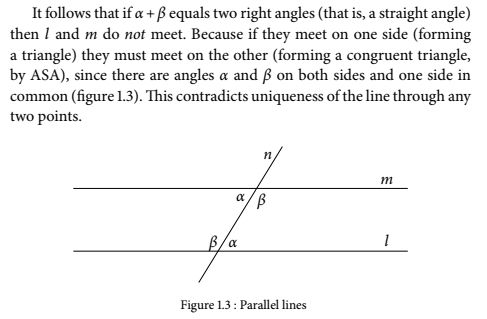
So, as I say, he does not use the parallel axiom to prove that the two lines with a+b equal straight angle, do not meet. He rather proves this first. He uses the parallel axiom to prove the converse, i.e., if the sum is not equal straight angle, then they meet. Here:
-
Parallel axiom
The only such connection I see is, if the ASA for triangles depends on the parallel axiom. I don't know if it does. It seems that "it follows" of Stillwell is misleading, and all he wants to demonstrate is why Euclid postulates the case of a+b being less than two right angles. P.S. Nope, this understanding is also not right, because the next he says, "Thus Euclid’s axiom about non-parallel lines implies that parallel lines exist." How?
-
Parallel axiom
Where is an assumption that the parallel axiom is valid for a+b equal two right angles made? The only assumption made is that when a+b equal two right angles the lines meet, and this assumption leads to contradiction.
-
Parallel axiom
IOW, you also think that this statement of the parallel axiom does not apply in this deduction of the two described lines not meeting. There is no question of extending the parallel axiom statement to the case of straight angle. The question is, why Stillwell says, "it follows"? And this deduction does not use the axiom that if the sum of alpha and beta is less than two right angles then m and n meet. Or does it?
-
Parallel axiom
My question is, where this axiom is used in this deduction?
-
Parallel axiom
Sorry, I don't understand your question and its relevance to my question.
-
Parallel axiom
But it, supposedly, shows that not meeting of the lines in the case when sum of the angles is straight follows from the parallel axiom, which describes a case when sum of the angles is less that straight. How come?
-
Parallel axiom
Stillwell in "Reverse Mathematics: Proofs from the Inside Out" states Then, he deduces My question is: where in this deduction the parallel axiom is used? Am I blind? Please help.
-
Erich von Däniken has died
This movie caused some heated debates in my youth. Воспоминания о будущем (1970) I was firmly in the sceptics' camp.
-
Using Grok as a tool.
This study does not mention at all the sense of rotation. It does not relate to the topic in question, i.e., is irrelevant and does not help. Other suggestions in are not helpful as well.
- Using Grok as a tool.
- Using Grok as a tool.
-
Why do medication have side effects?
Answers on the Internet: Explainer: how do drugs work?
-
Why do medication have side effects?
Why do treatments cause side effects in the body?
- My Doctor says I'm.......
-
Why do people get the cold and flu in the winter time?
We, in a warm tropical country, have rather a "high season", when herds of tourists from cold countries come in carrying the virus with them.
-
3D vector product preserving length
"Show that such a formula for three squares is impossible as an identity in the polynomial ring in 6 variables over Z."