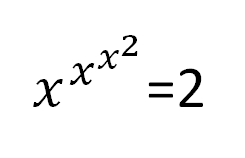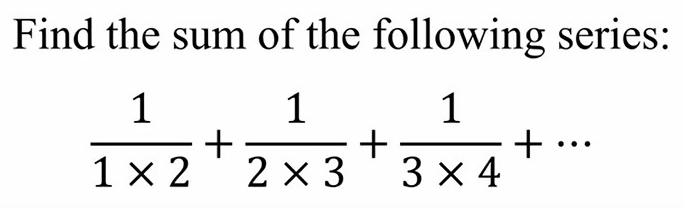Genady

Because the sets which appear on the rows in the new list are different from the old list.

That proof has to be modified for the new list. When modified appropriately, it works just fine. I don't see a problem.

Absolutely. I think that has been established some time ago, hasn't it? Why but? It doesn't contradict anything, does it?

The answer is in this statement: This statement means that for every natural number there is a row in the list. That row, by construction, contains that number. Consequently, every natural number is present in some row in the list.

I'm afraid I don't understand what you mean by "list of each set". What I see in your last presentation is a list of rows. Each row contains a number and a set. Each set contains one number. For example, the third row contains the number 3 and the set {3}. The set {3} contains one number, namely, 3. There is nothing else in this set. An arbitrary n-th row contains the number n and the set {n}. The set {n} contains one and only one number, the number n, and nothing else.

Yes, but not in my case.

Cremation.

Is it a Haiku? Nice periodic table I am Learn easily Understand

PS. @Boltzmannbrain, since you seem to like infinities, you might find it interesting.

OK then. Consider the other challenge: prove that it is impossible. IOW, prove that any shape with area <1 can be placed on the plane without touching the grid.

Hint: if you think to take the cube of this expression, you are on the right track.

This is a short-term future, isn't it?

However, as of today, there is no intelligence in "artificial intelligence". It is marketing gimmick. See for example, There’s no such thing as Artificial Intelligence – Australian Data Science Education Institute (adsei.org). Some quotes:

I wouldn't say in this case, "as n goes to infinity", because n doesn't "go" at all here, but rather is one arbitrary member of the set / sequence. Also, the expression, "for all n element of N", doesn't make sense to me in this case. One could write that there is mapping from the set N to set of rows such that every n in N is mapped to a row {1,2,3, ..., n}. See, e.g., Mapping | mathematics | Britannica.

If we will continue the discussion of my proof that the set S is not in the list, the following clarification of the list might help: l=1 L={1} l=2 L={1, 2} l=3 L={1, 2, 3} l=4 L={1, 2, 3, 4} ... Or, equivalently: l=1, L = {x| x∈N & x≥1 & x≤1} l=2, L = {x| x∈N & x≥1 & x≤2} l=3, L = {x| x∈N & x≥1 & x≤3} l=4, L = {x| x∈N & x≥1 & x≤4} ...

The last two lines above are wrong. The set on the line 5 in your list is {1, 2, 3, 4, 5}. This is the set L for l=5, i.e., L = {1, 2, 3, 4, 5}.

L does not have to be in S, and it not in S. L is a set on a line in your list. Each line in your list has a set. L is one of these sets, the one on the line number l.

No, l is not a sequence. It is a number. It is a number of some line in your list. We don't know which line it is, thus we call it l.

L is not a line in S. L is a set on a line number l in your list. If this is clear, I'll go to the second question.

It is not 1, it is l (the letter): L = {x| x∈N & x≥1 & x≤l}

I don't know what you mean in the second statement, but here is a proof that this set is not there. Let's define the set: S = {x| x∈N & x≥1} Let's assume that the set S is in the list. Then there is a line, l, in the list with this set on it. The set on line l is: L = {x| x∈N & x≥1 & x≤l} But L ≠ S which contradicts the assumption. Thus, S in not in the list.

This is wrong, i.e., not every possible set of increasing natural numbers (that increase by 1 starting from 1) is there. The set {1, 2, 3, 4, ...} is a possible set of increasing natural numbers (that increase by 1 starting from 1), and it is not there.

I got a simple solution, perhaps the one you have in mind:

These facts: my father died on my daughter's birthday, and my son was born on my mother's birthday.