Everything posted by Genady
-
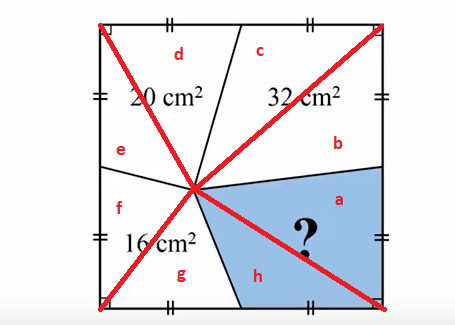
Find the missing area
As we don't have much to do with areas of arbitrary shapes like these, but we know much about areas of triangles, let's make the triangles: The triangles above are named, a to h. The puzzle is, to find the area a+h.
-
A grid and a shape
Thank you for asking clarifying questions. There are no gridlines here, only the points, which are the intersection points of the 'imaginary' gridlines. The shape should not intersect any of these points. BTW, to be sure, the OP question has been changed to this: prove that any shape with area <1 can be placed on the plane without intersecting these points.
-
Confusion with finite sets vs an infinite set of natural numbers
I certainly agree with you that there is no issue, and I don't try to guess what the fundamental misunderstanding is, but the OP asked to point to an error in his construction, if there is one. I use sets to formalize his construction to point out the error.
-
Find the numerical value
It doesn't let me see the whole step-by-step solution, but it looks like it just keeps simplifying the original expression. If so, it misses the beautiful insight: after the first step of taking the cube, the puzzle boils down to the simple equation, which is quickly solved by inspection.
-
Find the numerical value
What do you mean, it solves them right away?
-
Find the numerical value
So, after taking cube of the expression in question, and simplifying, we get it (i.e., the cube) being equal to Do you see something peculiar here?
-
Confusion with finite sets vs an infinite set of natural numbers
No, I don't know.
-
Confusion with finite sets vs an infinite set of natural numbers
If we define "a type T set" to be "a set of numbers from 1, increasing by 1, up to a finite number", then there is no infinite set of type T.
-
Confusion with finite sets vs an infinite set of natural numbers
Yes, it is. But there is no such set in your construction. IOW, there is no set in your construction "that starts at 1, increases by 1 and has infinite elements."
-
Confusion with finite sets vs an infinite set of natural numbers
I understand. There is no set equal to N in your construction. There is nothing to compare to because there is no infinite set in your construction that starts at 1 and increases by 1.
-
Confusion with finite sets vs an infinite set of natural numbers
There are never infinite elements and so no such n is needed. There is no such jump.
-
Puzzle for the Day
A.I. says,
-
How does ChatGPT work?
It doesn't go through the entire NN every time, but rather a random subset. So, it produces different response every time you run it. I got a similar, correct answer on the 6th trial.
-
A grid and a shape
Any comment? Question?
-
How does ChatGPT work?
This is a possibility. Or, just hanged around with a black hole for a while.
-
How does ChatGPT work?
Yep. This reminded me of my physics teacher who liked to say, "When I ask them any question, they give me any answer."
-
A grid and a shape
You are right. +1 Here is my take:
-
Confusion with finite sets vs an infinite set of natural numbers
Because it never goes from R to N.
-
Confusion with finite sets vs an infinite set of natural numbers
This does not exist. It never happens. There is no such symmetry breaking. There are only finite numbers of elements in R on the left side. As has been said above, R(n) is always finite. There are only R's on the left, never N.
-
Confusion with finite sets vs an infinite set of natural numbers
Yes.
-
Confusion with finite sets vs an infinite set of natural numbers
R(n) does not change to infinite. R(n) and {R(n)} are different things. The former contains numbers in the range [1, n]. The latter contains sets R(n) for all n's. The former is finite, the latter is not.
-
Confusion with finite sets vs an infinite set of natural numbers
Correct. R(n) is finite. {R(n) | n∈N} is not. R(n) = {1, 2, 3, and all other numbers up to n} LIST = {R(n) | n∈N} = {R(1), R(2), R(3), and all other R(n)'s}
-
Confusion with finite sets vs an infinite set of natural numbers
This last example not only is not permitted, but it does not have any meaning in the set of natural numbers. Infinity is not an element of this set. This example does not make sense. Yes, each R(n) has n elements. None. Each R(n) is finite.
- anti matter
- anti matter