-
Posts
25 -
Joined
-
Last visited
Contact Methods
-
Website URL
https://sites.google.com/view/jyboulay/accueil
Profile Information
-
Location
FRANCE
-
Interests
Genetic code. Primes numbers. Number theory. Symmetry.
-
Favorite Area of Science
Mathemetics
-
Occupation
social worker
Jean-Yves BOULAY's Achievements

Quark (2/13)
-2
Reputation
-
Symmetry Culture and Science 34(1):061-086 By proposing a numbering of the twenty proteinogenic amino acids deduced from the physicochemical properties of the four coding DNA nucleobases, it is established that this amino acid number, equal to 5x entities, is not arbitrary. Indeed, we demonstrate that many attributes of these twenty amino acids, as a whole, are also 5x in number and that by isolating, since their numbering, the 3x peripheral amino acids from the 2x internal ones, these attributes are divided into ratios of 3/2 as exact value. This is verified both as the physicochemical properties of the 20 amino acids and as the coding configurations of the nucleobases, the source of this numbering. https://www.researchgate.net/publication/370897007_Numbering_of_the_twenty_proteinogenic_amino_acids_and_new_alphanumerical_nomenclature_proposal_to_them Depending on their numbering (external or internal): synthesis of the distribution of the prime attributes (to 5x in number) related to the 20 proteinogenic amino acids in exact 3/2 ratios.
-
Jean-Yves BOULAY started following Chevron Form Quantum Charts
-
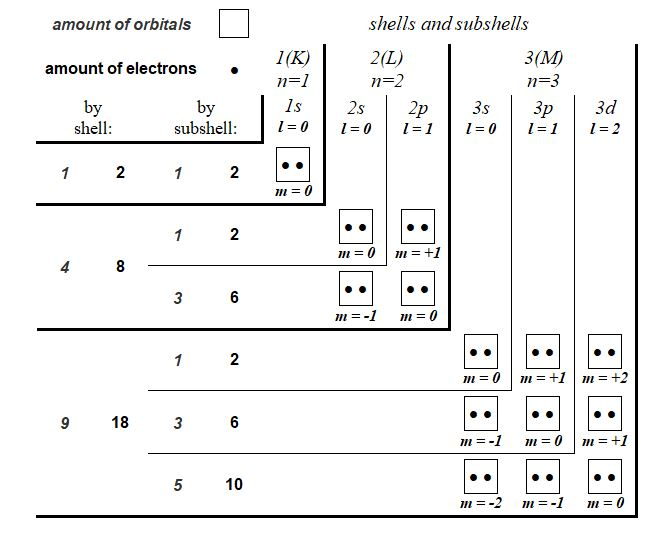
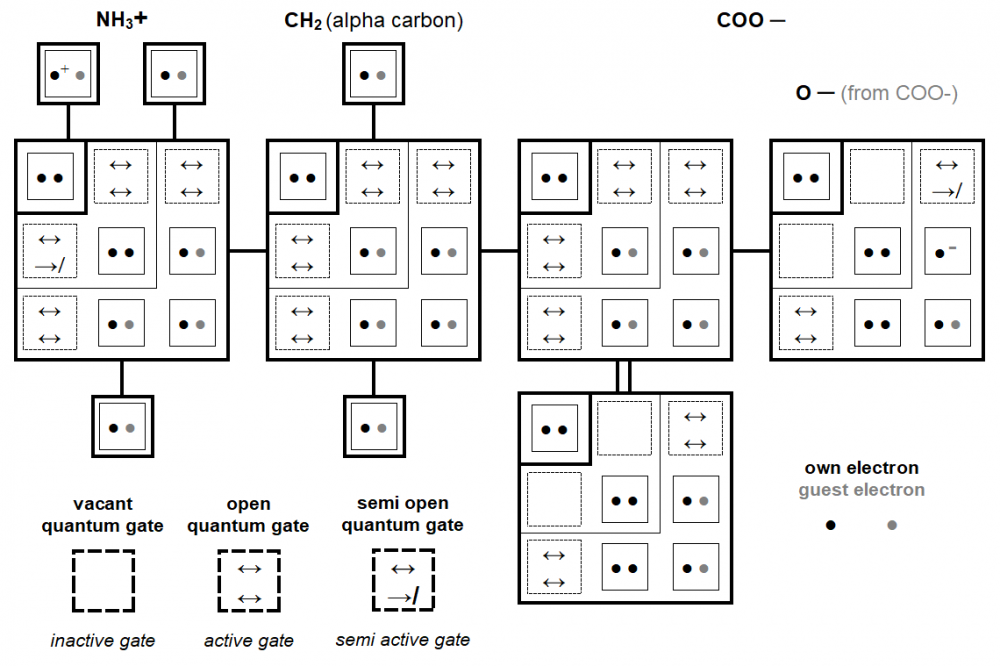
It is proposed here to represent the quantum distribution of atomic orbitals in an unprecedented table where the quantum shells and subshells are drawn in the form of chevrons whose vertices are occupied by orbitals with the magnetic quantum number m = 0. This new representation visually shows, much better than a classic linear chart, the relationship between the number of quantum shells and the number of orbitals . Also, this new visual model can be easily used in the individual quantum depiction of the atoms represented alone or into molecules and can find its place in illustration of some two-dimensional space-time quantum theories. Finally, this graphic representation allows to introduce the hypothesis of the existence of stealth orbitals, quantum gates opening towards singularities. full paper: https://www.researchgate.net/publication/346080523_Chevron_Form_Quantum_Charts In the scientific quantum literature, many tables already exist describing the quantum structure of matter. Very often, these tables are represented in the same general linear form to describe the distribution of orbitals and electrons on the different quantum shells of chemical elements. The quantum study of the genetic code [1] has was an opportunity to propose a new type of table describing the quantum organization of atoms. We will demonstrate here, after having compared it to a classical illustration, that this new concept of chart, using an innovative representation of quantum shells arranged in the form of chevrons is more explicit in the study of chemical elements and molecular chemical structures. Classical versus chevron form quantum chart Figure 4 can would be without from comment. Compared to the classic version, the chevron form version of the quantum chart brings a vision as in relief of quantum shells (See Chapter 3.1). In this new version, for each quantum shell, the orbitals appear as a compact square block whose dimension is directly proportional to the shell number (square power). Also, orbitals with the same magnetic quantum number (m) are arranged on the same diagonals. All of this is instantly visible in this chevron-shaped version, unlike the linear classic version. General chevron form quantum chart Figure 5 shows the chevron form quantum table of the first 15 electronic shells. This graphic concept is extensive development of that introduced in Chapter 2.1 and illustrated in Figure 2. We suggest that this new graphic type be favoured for the description of the quantum organization of the different chemical elements. Atoms quantum charts In this new quantum chart concept, and more generally in the quantum study of the chemical elements [1], the electronic spin is so not detailed (by ascending or descending arrows). In return, it is the migratory or non-migratory nature of the electrons which is highlighted. Thus, for example, representation of the nitrogen atom and sulphur atom such as that illustrated below (Figure 7) is favoured. With this new quantum chart design, the relative dimension of quantum shells and subshells is also more explicitly perceptible than in a line graph (such as the one presented in Figure 1). In Figure 8 is illustrated, in the new chevron form chart concept, the quantum structure of the first ten chemical elements. This type of table gives simultaneously, visually, a lot of quantum but also physical information, in particular a good idea of the electronic wingspan of the different chemical elements represented. Molecules quantum charts From the atoms quantum charts in chevron form (see Figures 7 and 8), then we propose a representation of molecules under the aspect of that presented in Figure 10. This does not represent molecular orbitals but describes the source orbitals of each atom. Again, the chevron-shaped representation of quantum shells, subshells, orbitals and electrons distributed over them appears clearer than a linear or circular representation of atoms. Stealthy orbitals hypothesis Stealthy orbitals concept introduction This new graphic chevron-shaped representation of the quantum organization of electronic shells is the opportunity to propose the hypothesis of the existence of stealthy orbitals. We therefore propose the existence of two additional stealth orbitals on each end of the quantum subshells, this excepted for the very first subshell 1s. Figure 11 illustrates this concept for chemical elements Nitrogen and Sulphur as example. These stealthy orbitals can be considered as quantum gates where pass electrons changing orbital and subshell, especially in their interatomic migrations. Although these "quantum gates" graphically (in square shaped) fill the chevrons so as to close the quantum shells, they are not affected by the different quantum numbers applied to the electrons. Any of these gates can be therefore taken by any single electron within a shell. Beyond and through these quantum gates, the electrons pass through a singularity without classical spacetime and are therefore projected instantly from an orbital to another (outside or inside atoms). Stealthy orbitals concept depiction Into Figure 12 amino acid Glycine is depicted in its zwitterionic state. This doubly ionized state is a good way to illustrate the different possible configurations of stealth orbitals supposed to operate in the quantum subshells of atoms. Stealthy orbitals and singularity The stealth orbital hypothesis also requires us to propose the existence of singularities where electrons temporarily transit. The latter term is actually not really appropriate since we suggest that in these singularities there is neither time nor space. We therefore call them "singularities without spacetime". These singularities are therefore a virtual place (without space) where electrons pass when they operate in covalent bond. Figures 13 and 14 will now illustrate the quantum mechanism of these virtual entities. Classical functioning of singularities When two orbitals are in possible interaction, so stealthy orbitals activate and a singularity appears. In this new stealthy orbitals hypothesis, we suggest that the first orbital 1s is simultaneously also as a quantum gate (stealth orbital) but only when this orbital does is by only one electron, so in fact only for the hydrogen atom. Functioning of singularities in ionised configurations Figure 14 illustrates the interactions between orbitals of the Hydrogen in excess and of Nitrogen in the positively ionized NH3+ group and what happens to the celibate orbital of Oxygen in the negatively ionized COO- group of the zwitterionic Glycine introduced in Figure 12 and used as an example. In positive ionisation, an electron (·+) from Hydrogen atom (thus orbiting on a gate-orbital*) can generate a singularity towards a quantum gate (of a non-hydrogen atom, in the example: Nitrogen). But this one, not being connected to any orbital, stays on its orbital. Nevertheless, a non-binding bond is possible between the two atoms because an electron of Nitrogen atom (from a full orbital) can cross the singularity to join and share the celibate orbital of Hydrogen atom. In negative ionisation, a celibate electron (·-) from the third Oxygen subshell activates a gate and a singularity. But this gate remains semi closed (so, as far as, semi open) and the electron cannot penetrate or cross the singularity because there is not another activated gate (stealth orbital) due to the absence of a Hydrogen atom where it can migrate. So this electron stays on its orbital and none bond is created. However, the non-filling of the orbital in Oxygen, leave open a passage in the singularity and in the quantum gate which therefore remains semi open. *Recall: it is agreed that, in Hydrogen atom, the first orbital 1s is simultaneously also as a quantum gate (stealth orbital). Functioning of singularities Some way, one can say that various configurations illustrated in Figures 13 and 14 are as molecular orbitals. So, from the stealth orbitals hypothesis, a molecular orbital is structured like this: orbital ↔ quantum gate ↔ singularity ↔ quantum gate ↔ orbital As the light wave is an emanation of the photon, the singularity is an emanation of the celibate electron. Also It is the singularity, emanation of a electron, that activates the gates between celibate electrons. but these quantum gates are not emanations of electrons, they are in a vacuity state. Stealthy orbitals and chevron form quantum chart The hypothesis of stealth orbitals allows us to offer a more quantum chart trimmed and still in chevron form.
-

Genetic code, quantum physics and the 3/2 ratio
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
Scientific research is not limited to publications in journals. I believe you have not read the article because you will find in it that all the data is correct. And now that this post is in the speculation category what's stopping debating it. (also, publishing in journals is very tedious, have you tested ...) -

Genetic code, quantum physics and the 3/2 ratio
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
If this is numerology, then so is the Periodic Table of Elements! The first two primes for example. and 2 + 3 = the 3th prime. Just 5 is sum of two consecutive primes. Have you a published paper for give lesson?- 10 replies
-
-2
-

Genetic code, quantum physics and the 3/2 ratio
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
When I show that the components are in opposition of the arithmetic 3/2 ratio, there is nothing speculative about it! What is there speculative in this representation? -

Genetic code, quantum physics and the 3/2 ratio
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
This study describes the real structure of the atomic components working in the genetic code. Everything that is presented there is completely correct. This post did not have to be moved to the "speculations" section but was in its place in biochemistry and molecular biology! This post is unfairly placed in speculation. Please let me know what information is wrong or not verified in this article. -
The analysis of the quantum structure of the five atomic elements composing the coded twenty amino acids and the four coding nucleotides of DNA working in the organization of the genetic code reveals an opposition of their respective constituents in always an arithmetic ratio of value 3/2 according to the parity of the number of their quantum shells. Also, the quantum analysis of the amino acid Glycine, the smallest component of peptides that can be confused with saturated base, reveals the same arithmetic oppositions of 3/2 value of its components by the differentiation, operated according to their number of protons, of its five chemical groups. Genetic code, quantum physics and the 3/2 ratio Quantum analysis of the atoms constituting the genetic code Jean-Yves BOULAY Genetic code quantum analysis.pdf Within the mechanism of the genetic code and therefore among the twenty amino acids, Glycine is distinguished by its absence of radical. Its radical is reduced to a simple hydrogen atom which in a way simply closes the "base" structure common to each amino acid. The quantum study of this glycined base, identifying with Glycine, reveals singular arithmetic arrangements of its different components. New quantum chart This quantum study of the genetic code is an opportunity to propose a new type of table describing the quantum organization of atoms. In this chart, illustrated in Figure 5, the different quantum shells and subshells are presented in the form of chevrons. At the top end of each rafter are indicated the names of the different shells and subsells; at the left end of these chevrons, the numbers of orbitals and electrons of these different shells and quantum subshells are indicated. At each chevron vertex is the orbital where the quantum number m = 0. The orbitals with positive quantum number m are progressively positioned towards the top of these chevron vertices and the orbitals with negative quantum number m are progressively positioned towards the outside left of these chevron vertices. In the appendix, the same type of table is presented describing the quantum organization of the shells and subshells up to the 5th shell (O) and 15th subshell (5g). This innovative presentation, more explicit in describing the quantum structure of the atomic elements, will be used in various tables of this quantum study of the constituents of the genetic code.
-

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
Initial arithmetic arrangements in 3/2 ratios inside hierarchical classification of whole numbers. From the new paper:https://www.researchgate.net/publication/341787835_New_Whole_Numbers_Classification -

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
-

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
I obviously encourage anyone to explore further beyond. My article is only the beginning in this way and I work myself (and I have already discovered) on other phenomena including especially with the concept of Sophie Germain numbers. -

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
In my introductions and conclusions I insist that these phenomena are related to the decimal system and therefore to small closed matrices of 5x or 10x entities. This is the basis of the article which does not study long sequences but their start (in multiples of 10 or 5). -

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
I have worked on other matrices but there are more significant results with matrices to 10 by 10. But see above there is also with 5 by 5. "so-called, "thus-called" these grammatical problems are secondary. -

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
The association of the numbers 0 and 1 with the primes, then the distinction of 4 classes of numbers, allows many arithmetic singularities. 3/2 ratio, this term appears hundreds of times in this article! It is always involved between and in sets of entities of 5x sizes (so 3x + 2x) including, in most situations, various matrices of ten by ten entities. These arithmetic phenomena demonstrate the equality of importance of the different types of entities studied as the ultimates or non-ultimates, the primordials or non-primordials, the digit numbers or non-digit numbers among the fundamentals, the numbers of extreme classes and those of median classes, fertile or sterile numbers, etc. . Thus is revealed in this article quantity of dualities distinguishing whole numbers in always pairs of subsets opposing in various ratios of exact value 3/2 or, more incidentally, of exact value 1/1. Also, many of the phenomena presented, in addition to involving this arithmetic ratio of 3/2, revolve around the remarkable identity (a + b)2 = a2 + 2ab + b2 where a and b have the values 3 and 2. This generates many entanglement in the arithmetic arrangements operating between the different entities considered and therefore strengthens their credibility by the dimensional amplification of these arithmetic phenomena. -

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
Please, sorry to repeat again and again: read the entire article carefully.- 38 replies
-
-1
-

New whole numbers classification
Jean-Yves BOULAY replied to Jean-Yves BOULAY's topic in Speculations
When I said: 0, 1 and all primes not admit any non-trivial divisor (whole number) being less than them. Why are You so afraid of this? So also answer this question: is it right or not? If this is true then the whole numbers divides well into two groups: ultimate and non-ultimate numbers. Yes of course: number 0 !