-
Posts
511 -
Joined
-
Last visited
About TakenItSeriously
- Birthday 03/12/1964
Profile Information
-
Location
Silicon Valley
-
Interests
Problem Solving, Poker, Physics, Engineering, Digital Security
-
College Major/Degree
autodidact
-
Favorite Area of Science
Physics
-
Biography
Learned SR, GR, & QM at age 7. Resolved myself to altruism over religion the age of 17. Solved EMI issues for Gigabit Ethernet which had blocked its rollout for two years.
-
Occupation
Retired
TakenItSeriously's Achievements

Molecule (6/13)
9
Reputation
-

Corona virus general questions mega thread
TakenItSeriously replied to FishandChips's topic in Microbiology and Immunology
According to worldometers.info on 03-22-2020 @12:30 afternoon which is the top site from a google search of “coronavirus numbers” Total Cases: 321,278 Active cases: 211,573 Recovered: 96,006 Deaths:13,629 First of all, I am not a doctor nor am I mathematician. However, I was tested as profoundly gifted at logic in college which means that I have a knack for problem solving. These numbers are based on only what we know as reported by governments around the world. Of course the numbers may not be accurate due to political fudging and of course testing is not anywhere close to 100%. However, it seems to me that the odds of dying after testing positive is not really around 4% as reported by most media outlets. This number seems to be a best possible spin of the numbers i.e. # of deaths divided by total cases: 13,629/321,278 = 4.264% I believe this is the wrong way to calculate the numbers because it includes the 211,573 of active cases which are uncertain as to whether they will result in a recovery or a death. If you test positive and you ask the question: what are the odds of coming out alive when all is said and done then a more accurate prediction should be the number of deaths divided by (the number recovered plus the number of deaths). 13,629/(96,006+13,629) = 13,629/109,705 = 12.49% Now to be fair, there is quite a large lag-time between the number dead to the number recovered because it’s early in a growth dynamic scenario where death generally occurs much more quickly than recovery so we can probably assume the recovery number should be much higher but still, I think the most accurate number should be something like somewhere between 4.3% and 12.5%. Thoughts? -

The Anti-verse is getting attention
TakenItSeriously replied to TakenItSeriously's topic in Speculations
Swansont, Thank you for your reply. You asked some difficult questions all of which I may not be able to answer to your complete satisfaction right now despite having thought about this problem for over two decades but I will do my best to answer what I can and perhaps I, or others, will be able to contribute more at a later time. Iv’e often wondered if it could ever be 100% finished or would there always be more questions that needed answering? Perhaps the later is the case because it seems unlikely to me that mankind was ever meant to know everything. Perhaps we are only meant to forever struggle to increase our knowledge by just enough to solve the latest problems that we’re confronted with in order to survive as a species. You have to understand that it’s only deterministic from a point of view from someone who exists outside of time. From the point of view of an observer in either universe, they cannot know their future precisely because according to Heisenbergs uncertainty principle, we can only know half of the information needed for a single particle. Only an omniscient being who exists outside of time can entirely have access to complete information. That’s what I mean by sharing a single deterministic future. They would not be two independent universes like we might think with the many worlds interpretation, but be linked by their entanglement and exist together like two sides of the same coin. Once entanglement is broken, then the information each universe has may be more definitive and less probabilistic but each universe still only has access to half of the information needed to precisely predict the future. I’m not entirely sure what you mean. I can say that the two cones represents two opposite directions in time, not two opposite directions in space. Also, you shouldn’t think of them as two arbitrary different times but a single differential time. So, in essence the anti-verse exists everywhere around us only in differential time with half of it phase shifted by 180° causing it to be hidden from direct observation except through the evidence of how they interact through their electromagnetic fields in their exhibiting quantum spin or intrinsic dipole moments. They exist in a virtual dual orbit due to their electromagnetic fields and entanglement interacting with both particles at once. -

The Anti-verse is getting attention
TakenItSeriously replied to TakenItSeriously's topic in Speculations
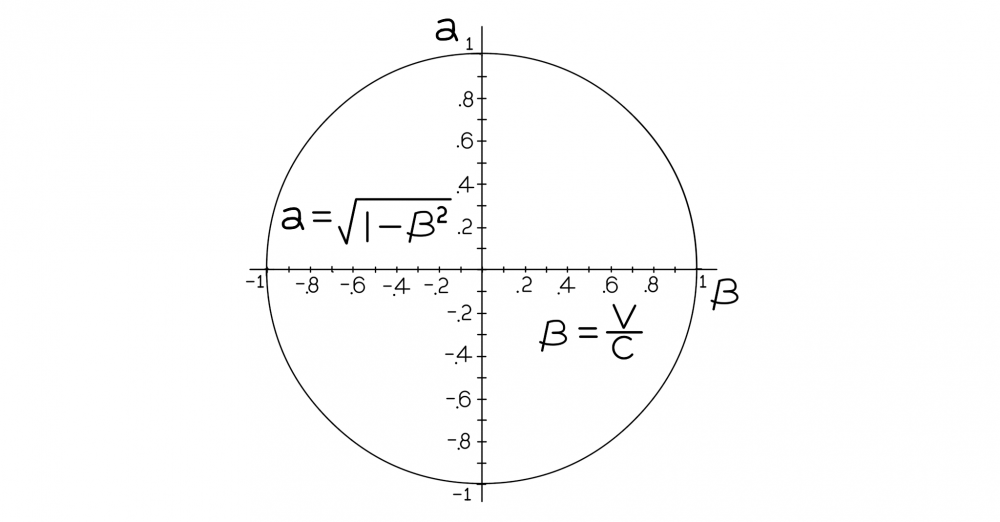
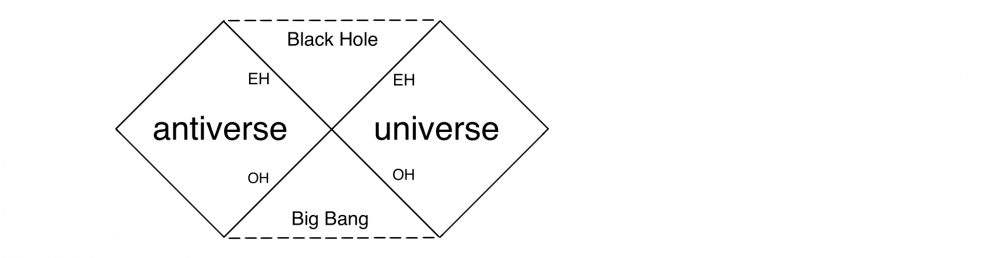
Now that I just posited that relativistic effects are directional: Are relativistic effects directional? If that were true and length contraction represents one side while time dilation represents the other side and the top half represents the universe while the bottom half represents the anti-verse. Then, in that case, the full plot of α vs β makes sense as a unit circle: I didn’t want to introduce this plot in the other thread because I didn’t want to suggest that positive/negative α represented directionality. positive/negative β represents directionality. The Penrose diagram shows the role of the anti-verse with black holes. -
TakenItSeriously started following The Anti-verse is getting attention
-
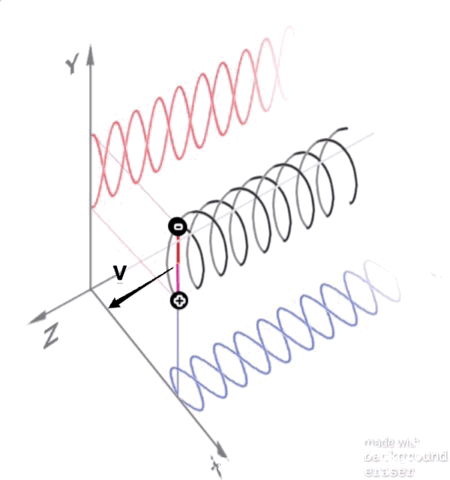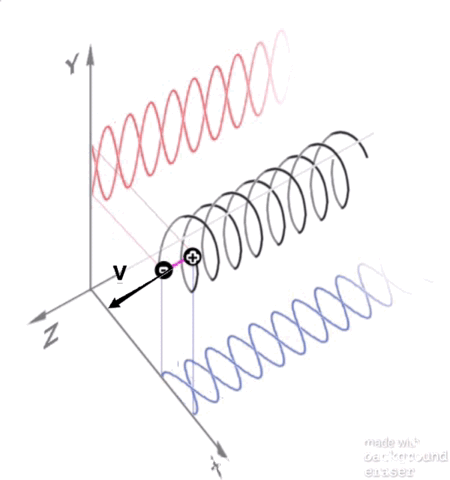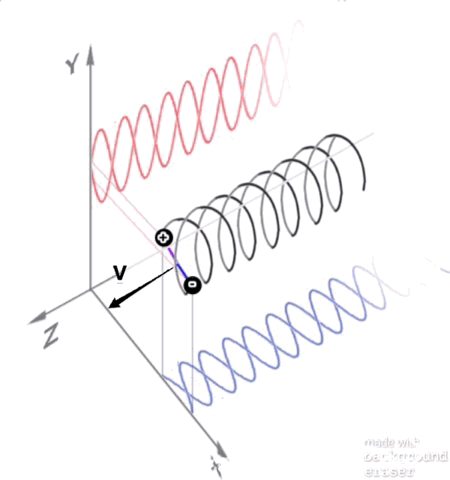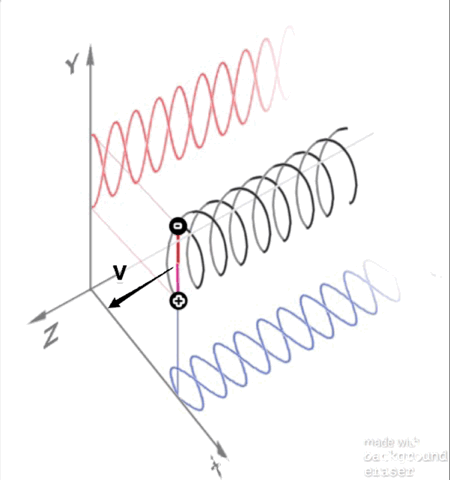
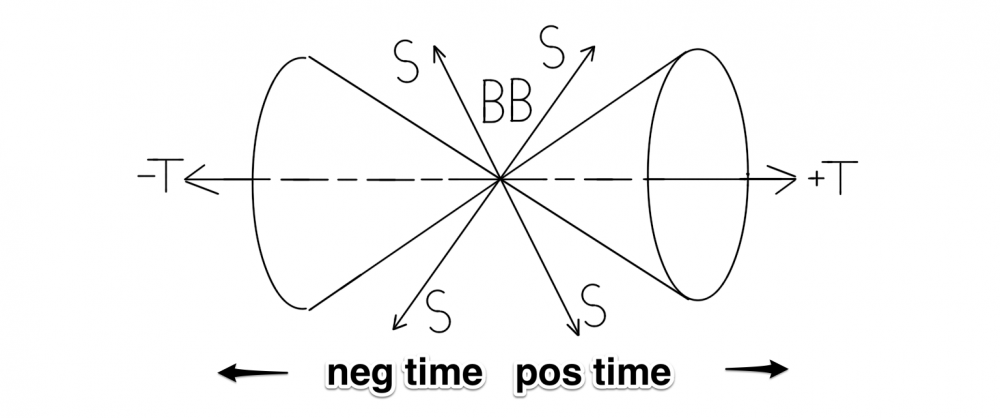
My hypothesis of an anti-verse which I first posted about here: Why would we expect an anti-universe to be detectable? and written about many times since elsewhere, is getting the attention of cosmologists: Our Universe has antimatter partner on the other side of the Big Bang My hypothesis, in part: The first mystery of the Universe that is still unresolved today is what happened to all the antimatter created by the Big Bang? Quantum Mechanics tells us that matter and antimatter was created in equal parts as entangled pairs by the big bang at the beginning of time yet there is absolutely no evidence of the existence of all that anti-matter today. One theory suggests that it was all annihilated and due to an imbalance of more matter than antimatter, or 1 extra particle of matter per billion matter/antimatter pairs was enough to leave us with all the matter in the universe today. However, all attempts to prove this imbalance have failed and, in fact, all evidence thus far seems to suggest that their was no imbalance. Instead the following noted works seem to suggest something else: CPT symmetry mathematically proves that an anti-verse must include symmetries of charge conjugation, parity transformation, and time reversal. Noether’s theorem had mathematically proved that the Universe must be symmetrical according to the laws of conservation. Richard Feynman had once posited that antimatter is exactly like matter existing in reverse time. Imagine for a moment that Feynman's statement was literally true? If the antimatter created by the big bang did exist in a state of reverse time, then if you think about it carefully, reverse time starting from the beginning of time would be a separate dimension of negative time. Another words if you count forwards from zero you get positive numbers but if you count backwards from zero you get negative numbers. ..., -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, +6, +7, +8, +9, +10, ... These two equal and opposite time lines (or more accurately time rays) would never overlap and so it wouldn’t be like reverse time as we normally think of it in terms of decreasing entropy like a broken glass reassembling itself and falling up to a table top. Therefore, it would not allow for paradoxes such as the grandfathers paradox. Both dimensions would be dimensions of an expanding universe and increasing entropy. Instead the hidden extra-dimension of negative time would be perfectly symmetrical to our universe in positive time due to its entanglement with our universe. Figure 1: A dual big bang model where matter expands in a dimension of positive time and the entangled antimatter expands in a hidden dimension of negative time. These two dimensions of time would not be two independent universes. Instead they would be linked to share single deterministic future by their entanglement. So as a whole, they would have a shared determinism. However, from the perspective of an observer in either dimension, half of all information would be hidden in the opposite dimension and uncertainty would prevent us from ever being able to predict our future. Another words, outside of time, the two halves together would constitute a deterministic universe but from the perspective of an observer in either half, there must be uncertainty and therefore we would have free will. So what would this anti-verse look like? According to CPT symmetry, to an observer in negative time, it would be indistinguishable from that of an observer in positive time. The consequences of a dual universe could explain all the weirdness of quantum mechanics to not seem so weird. For instance, in the dual slit experiment for every particle that goes through one slit an entangled anti-particle would go through the opposite slit and their entanglement would impart the information of both slits to both particles causing the wave distribution pattern. If a particle is observed going through a specific slit, entanglement would be broken and the result would be a dual distribution of particles. It would also answer how light particle/waves could propagate forever in a vacuum. Figure 2: An unobserved particle and antiparticle would exist together in a virtual dual orbit connected by their entanglement. This would immediately explain the properties of spin having a much larger radius of angular momentum that the size of the particle or why particles with a single charge would behave like spinning dipoles. The differential waves together would explain how they could propagate through a vacuum forever. Spooky action at a distance could be explained for particles in opposite dimensions of time, time would cancel out and the actions between two entangled particles would cancel out and much more.
-

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
That’s what I was trying to do. As I said, I meant to say the sentence was nonsensical as written, not the entire post, and I did say that I assumed it must contain some typos. Edit to add: I apologize for any confusion. -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
Janus Theres some confusion here on what was posted that I’d like to clarify before it gets out of hand. First, please refer to this post: When I was saying it was nonsensical I was referring to the particular sentence I quoted, not your entire post. After I posted it, I realized what you must have meant to say.... You used an ambiguous reference of “her” which could have meant Carole or Alice. I assumed you meant Carole’s point of view when I saw you refer to Alice in the same sentence. The problem was compounded when you mistakenly referenced that Alice was catching up to Bob. It’s a minor error, but when speaking in the context of SR, it becomes very confusing and that’s why I said it was nonsensical as written. I waited a while before replying trying to avoid a cross post. Unfortunately you were busy writing a long reply so my waiting only backfired. After rethinking the problem with the corrected sentence I compounded the cross edit with a cross post before seeing your long reply and posted an encapsulation of what I thought you were trying to say. So having said this, is that what you were trying to say, mor or less. -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
Edit to further add: So in the corrected context, I think the point you may be trying to make is that all three points of view on the problem tells a very different story which I agree happens a lot in SR. Kind of like the simultaneity thought experiments. So how valid could any conclusion be unless they all meet at some point which is impossible without adding acceleration into the problem. Is that about it? Ugh, cross posted. Sorry, I can take a while wile pondering the problem. -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
I assume this contains some kind of typos. I mean I think your saying that Alice’s perspective on Carole’s speed is 0.97561... c and vice versa which I understand without doing the math myself but the rest is nonsensical as written. Edit to add, after reading it a few times more I think you’re trying to say the following: From Alice’s perspective after passing Carole, Bob is receding at 0.8c and Carole is catching up to him at roughly 0.98c. Is that correct?- 88 replies
-
-1
-

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
Sorry, I think you made a mistake here. From Alices perspective: Alices travel distance on the outbound leg due to length contraction should only be 8 Ly*0.6 = 4.8 Ly therefore her travel time is 4.8/0.8 = 6 years. -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
Ok, I got it. For sure acceleration adds a ton of complexity to this problem. BTW it’s not a stable model unless you add a balancing mass on the opposite side of B, say B’ but thats getting a little nit picky. It reminds me of an even simpler model of two astronauts tethered together in flat space. Someone gives them a push and they start spinning apart putting tension on the tether and ending up in a dual orbit kind of like a binary star system. So what happens if you remove the surrounding universe from this model. They would have no reference frame to know that they’re even spinning and it would then seem as if they were just drifting in the void with a strange repulsive force that is pushing them apart. Others would argue that their would no longer be a repulsive force and they would just be floating together in the void with the tether limp between them. The point is that I agree that gravity or acceleration adds a ton of complexity to the problem. That’s why the three observer thought experiment (not mine BTW) was modified to only involve drift speeds taking acceleration out of the problem all together. https://en.wikipedia.org/wiki/Twin_paradox?wprov=sfti1. I will respond to your analysis of that problem next. I set the model up to be equivalent with the TP example you gave initially: Bob’s time on Earth is still 20 years. Essentially Alice’s travel time is 6 years, Carole’s travel time is a symmetrical 6 years so the total is12 years which is 60% of Bob’s time of 20 years. I can’t see how you derived the numbers in your analysis. Can you please clarify? -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
I agree, it can become a confusing mess. That’s why I like to break problems down to their simplest forms possible while still considering all relevant variables and points of view. I’m a little confused about what each clock is doing. Is it that the central clock is spinning around at the center point of centrifuge A. Another clock is revolving around the spinning clock at some radius on the perimeter of A A third clock is revolving around a separate centrifuge B and the two circular paths meet up like two spinning gears? -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
Damn, I lost my entire last post due to an outage. Hopefully I’m back now. #5 Regarding acceleration. I mostly agree especially with how it plays no role in explaining the time deviation experienced by the twins. Perhaps not as much as with the asymmetry of the other effects. Acceleration, while once accepted as the underlying cause, has since been refuted because of a modified TP thought experiment which removed all acceleration from the problem and you still end up with the same results. It adds a complex asymmetric effect to be sure but it’s irrelevant to the simple form of the problem when using only velocity. You can look it up here: https://en.wikipedia.org/wiki/Twin_paradox?wprov=sfti1 Under Twin Paradox subtitle: the Role of Acceleration. A synopses of the modified version includes three observers Bob at rest on Earth. Alice drifting past the Earth at 80%c on her way to the star 8 ly away. Carole drifting in the opposite direction at 80%c passes the star at the same time Alice passes it. Carole collects Alices information such as travel time, travel distance from the Earth, observations on Bobs time, etc. She then proceeds to Earth and passes all of Alices information as well as her own to Bob and the time experienced by both travelers only adds up to 60% of the time experienced by Bob. #6 I recall the Hafle-Keating experiment using jet airliners and atomic clocks and I agree that it does seem to represent a bit of a conundrum. However, I would question whether the time dilation measured was due to gravity or velocity. For example, I’ve been told that the time dilation calibrated for in GPS satellites is almost entirely due to gravity. I know, different elevations and speeds, but I just get the feeling that gravity still dominated time dilation in that experiment but IDK for sure. In any case, I’ve tried to consider how to adapt orbital information into the TP and it’s just beyond me so I let it drop and left the question to smarter minds to ponder than my own. Now we already agree that time dilation is the cause of the relativistic component of relativistic red shift. So how I would explain the cause behind the relativistic blue shift effect: Using the original example, Alice has just turned around and is headed for Earth. From Bob’s PoV: Alice is racing her own light traveling at 100%c while she is moving at 80%c. Another words it takes the light 8 years to reach Earth while it takes her ship 10 years. Therefore all of her transmissions on the return leg must be compressed into only two years. So this blue shift effect can all be explained by simple lag-time for the light to travel such a distance just like communications in our own solar system. No time dilation involved. However there is still the difference between relativistic blue shift and normal blue shift so what explains this difference. Well, Bob would expect Alices return leg to take 10 years which is squeezed into 2 years. However, after he meets Alice and counts the pings, he sees that there was only 4.8 years of pings compressed into those 2 years. As I mentioned before, the 60% of the time she experienced on her journey home is due to traveling only 60% of the distance due to length contraction. To look at it another way, we agree that: light waves from Alices ship exist in the space between Alice and the Earth. We agree that information is conserved and no waves (or pings) are either inserted or deleted. We agree that from Alices PoV the distance between the Star and Earth is length contracted to only 4.8 ly So what do you think happens to those light waves in length contracted space? The waves themselves must also be contracted...well at least those waves that are received from their sibling. You see the waves that are emanating from Alice’s ship are all part of the ships inertial reference frame. The waves that are emanating from Bob are all part of the Earth’s inertial reference frame. So from Bob’s PoV, the waves transmitted from Alice are length contracted. From Alices PoV, the waves transmitted from Bob are length contracted. Note that the waves coming from their own transponders are always pinging at 1 sec per sec. Another words the waves transmitted from their own transponders are all in each twins own respective inertial reference frame regardless of where they are in space. QED -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
The directionality I refer to is the relative type as in moving away from the observer vs moving towards the observer. In the problem from Alices point of view, you calculate length contraction for the distance Alice has to travel (in the direction of motion.) from Bobs point of view he knows the distance is 8 ly but he could calculate time dilation of a receding ship. -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
I agree and I’m not trying to say that it does. Strange was the one who was trying to assign meaning to the sign of the Lorentz factor. I only tried to tell him it doesn’t apply that way. Thanks. I’m going to have to get some sleep now. I’ll get back to this later. -

Are relativistic effects directional?
TakenItSeriously replied to TakenItSeriously's topic in Speculations
Because I guess he was associating the sign with directionality or something. The Lorentz factor as used in the TP doesn’t require a sign because it’s not a vector.