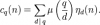Linear Algebra and Group Theory

I don't know the procedure to factorize: [latex]a^2-ab+b^2-bc+c^2-ca[/latex] into [latex](a+\omega b+\omega^2 c)(a+\omega^2 b+\omega c)[/latex] [latex]\omega[/latex] is complex cube root of unity: [latex]\omega^3=1[/latex] ============================================= Can all the quadratic forms be factorized with complex roots? [latex]ax^2+2fxy+by^2+2gyz+2px+2qy+d=0[/latex]

This should be laughably easy, but I am a little confused here. Suppose that the function [math]f: \mathbb{C} \to \mathbb{C}[/math]. Suppose further that [math]z \in \mathbb{C} = x +iy,\,\, x,\, y \in \mathbb{R}[/math]. What is meant by the complex conjugate of this function? My thoughts (such as they are!). Set [math]z = x +iy[/math], and set [math]f(z) = ax+iby[/math] and [math]\overline{f(z)}= ax-iby[/math] Apparently this can be written as the identity [math]\overline{f}(z) = \overline{f(z)}= ax-iby[/math], which I don't quite get. Moreover,...... ...... how does this differ from, say, [math] f(\overline{z}) =\overline{ax+iby}[/math]?

Let [V] a vector space over the field [F] and let [g] the polynomial on [F] given by [g (x) = a_0 + ... + a_nx a_1x + ^ n]. For each operator [T] on [V] defines a transformation [G (t): V -----> V] as [g (t) = a0 I+ a_1T +......+ a_nT ^ n] a) Prove that [g (T)] is an operator on [V] b) Let [a = a_0 + a_1 + ... + a_n] and let [E] a projection of [V]. Prove that if [n] is an even integer if [a = a_0], then [g (E)] is a scalar multiple of the identity operator.

If there are handy of R3 vectors: r1, r2, r3, r4, r5, r6 Which 3 of them barely envelop a specified vector: a? One can change all:( r1, r2, r3, r4, r5, r6, a) into unit vectors and compare, but it is too clumsy...

We've stepped into matrix operations this week and there are a few theorems that I don't quit understand. Now transposing a matrix is fairly straightforward and easy to comprehend, at least with small matrices. The part I'm having trouble with is the invertible matrix. I understand the key component that A^-1 is the inverse of A; however, I'm absolutely lost by the idea -- Ep...E2, E1A=In and the algebraic transformations of this equation. What is the purpose in finding the elementary matrix and what is a good way to visualize and understand this concept?

Hi all. I have something to ask about steady state vector. Say, we have a t.p.m. P = [1/2 1] [1/2 0] How to find the steady state vector s = [x] [y] for the Markov chain, given by the equation s = P s?

How did the author proved that L is a union of subgroups (shaded area in the image)? Thanks in advance.

Hi, How can I prove a certain abelian group is not free? If the given group is small, I can consider all the possible subsets of the group which are candidates to be the basis of the group and prove each of those cannot be the basis. As an example, if I consider the abelian group Z5 with addition, should I consider all the subsets of Z5 and prove that any of the subsets cannot be the basis?

This has kind of been bugging me fo a while. Let's say we have two groups and an isomorhism [math]\varphi: G_1 \cong G_2[/math]. If [math]H_1 \lhd G_1[/math] is a normal subgroup and we denote [math]H_2 = \varphi(H_1)[/math], then surely the quotient groups [math]G_1/H_1 \cong G_2/H_2[/math] are isomorphic as well. But what if we have a different isomophism [math]\theta: H_1 \cong H_3 \lhd G_2[/math]. Now we can't draw the conclusion that [math]G_1/H_1 \cong G_2/H_3[/math]. For example [math]\mathbb{Z} \cong \mathbb{Z}[/math] and [math]2\mathbb{Z}\cong 3\mathbb{Z}[/math], but clearly [math]\mathbb{Z}/2\mathbb{Z} \cong \mathbb{Z}_2 \ncong \mathbb{Z}_3 \cong \mathbb{Z}…

what are the applications of group theory in the field of computer science and how they applied in it?

Are special unitary groups as SU(5) symmetrical? Orthogonal groups are symmetrical but are unitary groups too?

Hello Everybody, I'm curious to know why we solve for the pivot variables when we reduce a matrix to reduced row echelon form and are trying to find a solution. Thank you

How do you write a strict subset symbol in latex?

Ok im quite confused on wrapping my head around the concept of subgroups. I mean i understand the definition and the general requirements that is needed in order to be a subgroup, but im lost when it comes to doing exercises, just cant seem to do them. So can anyone help me solve these two problems im somehow stuck at? 1. if [latex]H=[ x \in G : x=y^2[/latex] for some [latex]y \in G ][/latex] prove that [latex]H[/latex] is a subgroup of [latex]G[/latex] 2. Let [latex]H[/latex] be a subgroup of [latex]G[/latex] and let [latex]K=[x\in G: x^{2} \in H][/latex], prove that [latex]K[/latex] is a subgroup of [latex]G[/latex] given that [latex]G[/latex] is Abelian. Why does…

Need help on a problem and I think there's some notation issues I'm having: [math] A=\sum _{i}^{r}\lambda _{i}\bold{u_{i}v_{i}}^{T} [/math] where A is a nxr matrix with (left and right) singular vectors v_1... v_r, u_1...u_r & lambda are singular values How does summation work in this case? Each product of rank-1 matrices results in a vector which, when summed, should result in a vector. But A is a matrix, so I feel like I must be missing something very simple about matrix addition.

I have a question... now this is based on memory, if I have anything wrong, please correct me... We have natural numbers, then it is imaginary numbers, then we work with quarternions, then it's... Octonians and then it is the Cayley numbers? Is that right? I hope there is nothing inbetween... ... anyway, I understand imaginary numbers and quarternions, I am a bit vague on Octonians and how many numbers they involve... but why does everything stop at the Cayley Number... is it something to do with the Division Ring?

I have to either prove or disprove with a counterexample the following staement: "Let A be an m by n row-stochastic matrix in which all entries are positive real numbers and let B be an n by m column-stochastic matrix with the same feature. Then all the eigen values of the m by m matrix AB are real." Can anyone help? Please note that AB is not necessarily symmetric (Hermitian).

[math] \text {Proof that } a^2=b^3 \text { has solutions}, a, b = I > 1 [/math] [math] a^2=b^3 (1) [/math] [math] \sqrt{a^2}=\sqrt{b^3} [/math] [math] a=b^\frac{3}{2} [/math] [math] a=\sqrt{b}^3 (2) [/math] [math] b=4: (2) a=\sqrt{4}^3 [/math] [math] =2^3 [/math] [math] =8 [/math] [math] (1) a^2=b^3 [/math] [math] 8^2=4^3 [/math] [math] 64=64 [/math] [math] LS=RS [/math] [math] \text{Therefore proven} [/math] [math] b=9: (2) a=\sqrt{9}^3 [/math] [math] =3^3 [/math] [math] =27 [/math] [math] (1) 27^2=9^3 [/math] [math] 729=729 [/math] [math] LS=RS [/math] [math] \text{Therefore proven} [/math]

Hi All, I would like to know if there's anyone familiar with cosets and there properties. I want to actually explain few observations of cosets using linear algebra and if there's anyone familiar in this area please please reply. Thanks a lot.

Here's a new factorial function I invented that uses the Fibonacci sequence 1,1,2,3,5,... The Fibonacci Factorial, or Fib! is defined as the product of all the Fibonacci numbers up to n. Examples: 1Fib!=1, 2Fib!=1*1*2=2, 3Fib!=1*1*2*3=6, 4Fib!=undefined, 5Fib!=1*1*2*3*5=30 I don't know if this function would be useful for mathematics. Please give me some input. Isaac

In terms of the reference frame used in geometrical modeling, is there a difference between "Euclidian Geometry" and "Cartesean Coordinate Systems"? One thing I'm wondering is, how is Euclidian Geometry possible without a Cartesean Coordinate System? Yet, Descartes is credited with inventing the Cartesean system 2 millenium after Euclid invented his geometrical system. The Cartesean system cannot have been new in the 17th century - maybe given a new name, but not new.

I am currently studying Turing machines and I have set myself the following problem Using Pythagorian theory 1 Adjacent side = 12 inches Opposite = 12 inches Therefore hypononuse =19.7 (approx) 2 Adjacent = 1 foot Opposite = 1 foot therefore hypotonuse = square root of 2 which is a non computable 'irrational number' Same triangle - same dimensions First example - computable, second non computable - but the are the same. Go easy on me - my maths is not great... simple explanation appreciated. Zero

What are the more common theorems used to derive, for example a sphere in differential form, as a matrix representation? What are the more common expressions used to describe differential forms as matrices?

Hello, I have a linear algebra problem that I need help with. Basically, I need to get the eigenvalues and eigenvectors of several (sometimes tens of thousands) very large matrices (6^n x 6^n, where n>= 3, to be specific). Currently, we are just using MATLAB's eig() function to get them. I am trying to find optimizations for the simulations to cut down on computing time. There are three matrices that we use. H_constant - generated before the loop. Real and symmetric about the diagonal. Does not change after initial calculation. H_location - generated during each iteration. Diagonal. H_final - H_constant + H_location. Therefore, it is also real and s…

I am trying to work through multiple Schaums outline books on my own including Schaum's Outline of Differential Geometry. I cannot seem to get how to change basis in 3D vectors. From chapter 1, problem 1.47, Given vectors u1, u2, and u3 form a basis in E3 and v1 = -u1 + u2 -u3, v2 = u1 +2u2 - u3, v3 = 2u1 + u3, show that v1, v2, v3 are linearly independent and find the components of a = 2u1 - u3 in terms of v1, v2, and v3. END OF PROBLEM. Now that v1, v2, v3 are linearly independent is obvious since there is a zero coefficient for u2 in the equation for v3, and I can show that the determinate of the matrix formed by the row vectors (-1, 1, -1), (1,…