Everything posted by Enthalpy
-
Quick Electric Machines
More and more aeroplanes go electric, as the Beeb reports from Le Bourget bbc.com some claiming far better performance from battery-powered craft than my estimates here despite their wing isn't as wide. Hydrogen is missing in the report. Because of that, "electric" aeroplanes are said not to fly far, but the limit results from batteries. Hydrogen tanks and fuel cells give aeroplanes much more range than kerosene does.
-
String Instruments
Catalytic nickel protects against corrosion and is excellent against galling. I used some, with embedded Ptfe particles, at about 600MPa pressure and nearly no speed, against a martensitic stainless steel that galls horribly. The friction was tiny and very smooth without the stick-slip felt with zinc or phosphate layers against tempered steel. Embedded particles of MoS2 or graphite may be good too. Easy and smooth gliding would improve the bridges and saddles under the strings of some instruments. The piano uses steel nails to deflect the strings at the bridge. Wood receives already a gliding surface, the nails not, despite the force is bigger on them. Catalytic nickel with Ptfe should stabilize the tuning earlier. Some pianos have agraffes on the bridge instead. Same advantage. At least the cimbalum bends the strings over a metal rod at the many bridges. Easier gliding would equalize the tension among the sections between the bridges to improve the intonation. Especially important as the cimbalum has several strings per note. Many instruments have metal saddles or pins near the ends: harp, piano, cimbalom... where the deflection can be big. Better gliding would stabilize the tuning here too, just like violinists put graphite on the wood there. Tuning pegs would better rub smoothly too. They exist of hard wood or metal presently. At the violin, stick-slip of ebony pegs in the maple pegbox is a pain. But to replace ebony, nickel should rub strongly (no Ptfe), be black (graphite glides too easily), leave the fingers clean (embedded Ptfe doesn't). My gut feeling is that a hard polymer like LCP, possibly with a filler, has better chances than a metal. The piano, harp, cimbalom and others have metal tuning pins. Catalytic nickel protects against corrosion, rubs strongly without galling, and hopefully moves smoothly. Steinway pianos have already nickel-plated steel there. At string hooks, especially where piano strings make a U-turn without a knot, the strong friction of nickel might help tuning. Marc Schaefer, aka Enthalpy
-
String Instruments
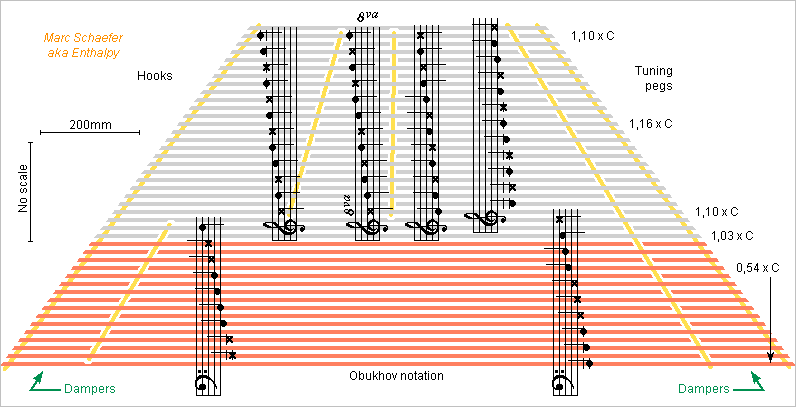
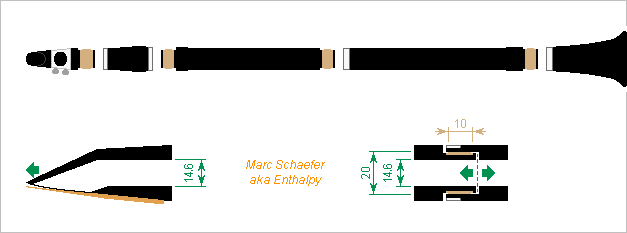
Here I propose a simpler notes chart for the cimbalom. The bass strands keep the usual positions up to B=234Hz, the rest differs: Semitones progress smoothly but for three jumps. At the jumps, the sections overlap by three semitones, similarly to trill keys at woodwinds. The sections have a constant interval. At the violin it helps. I imagine this chart makes the cimbalum easier to learn and play, but again I don't play it. Example of a usual (but incomplete) chart: beyondkarpaty.mutiny.net Hammered dulcimers would resemble more, but the intervals and bass strings differ. A pair of straight dampers can reach C=1051Hz while most Schunda-like models stop three semitones earlier. They are far from the struck positions. Schunda had achieved a nearly rectangular instrument shape at the cost of complicated notes chart and very inconsistent string sound speed even among consecutive notes. In my chart, the trapezoidal shape keeps the string sound speed between 1.10*C and 1.16*C at the treble and medium, varying very smoothly even at the section jumps, and decreasing gently to 0.54*C at the bass. Other string lengths would adjust these example figures, say between 1.20* and 1.27*. All bridges and saddles are straight on the drawing, but curves as at the piano could further equalize the string sound speed or limit the instrument's width. The outer bridges leave 10% non-speaking length in the corresponding strings, less than at a piano, but this can increase if accepting a slower propagation, at all these notes or only the lowest ones. Schunda's design has 39 strands, my chart has 43 with fewer spun strings. I suppose three strings per strand suffice. Marc Schaefer, aka Enthalpy
-
String Instruments
And oops. All pictures show one hook and one knot per string. Bad reason.
-
String Instruments
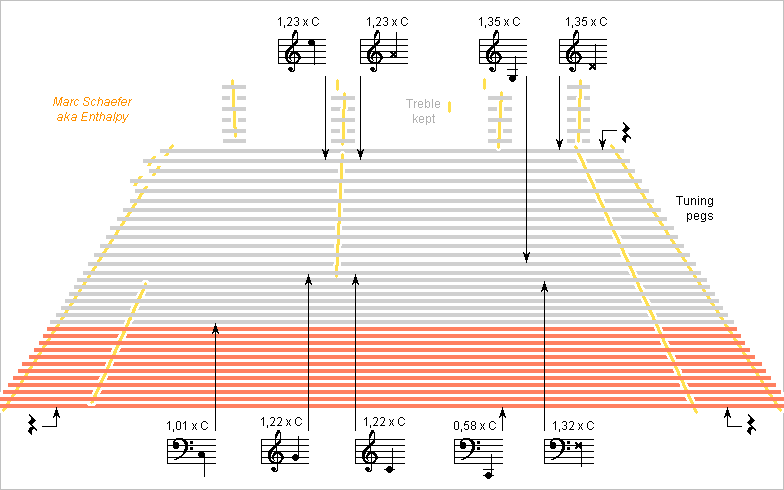
Here's a sketch of a big cimbalum that widens enough at the near strings to keep a good tension in the medium register, as suggested here yesterday. Its slope resembles much a small cimbalom. I fully ignore whether a wider instrument is difficult to play. If it helps to play near the centerline, the strings' tilt can be kept using taller bridges. For nicer and more uniform timbre, sound is here consistently 1.22* to 1.35* as fast in the medium strings as in the air. It remains faster than in air in half of the bass strings, whose plain steel saves money, then decreases in the spun strings to 0.58* at the lowest note. I'd keep the mass of the strings, that is, thinner if longer. Less stress is also welcome at the bigger frame. I've kept the distance from the bass bridges to the outer rails. Bringing less stiffness, strings passing the bridges straight might let shorten this distance. It is very short at a piano. Thanks to its metal frame, the piano also extends its soundboard very far under the agraffes and tuning pegs: to be copied if possible. Marc Schaefer, aka Enthalpy
-
String Instruments
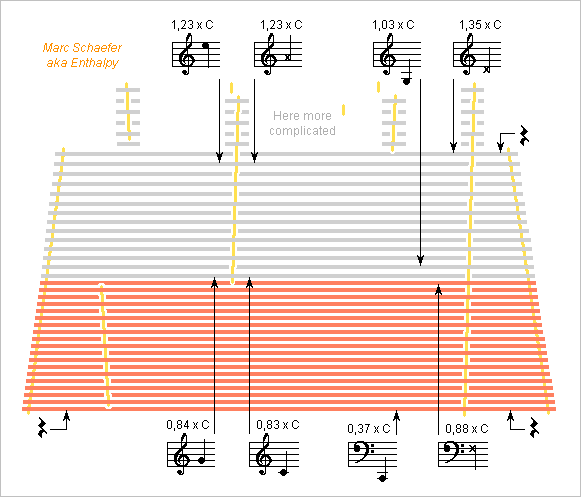
Here are some thoughts about the cimbalom. en.wiki - fr.wiki - cimbalombohak.sk - cimbalom.hu Big warning: I don't play the cimbalom nor any related instrument, so much here is probably b**ocks. If at the end one detail or an other makes sense, fine. Many instruments are called cimbalom, the name varies also much, and other instruments can be very similar. I consider the grand cimbalom, of Hungarian style, developed by Schunda around 1870. ========== If I see properly, the two sets of dampers are pushed down directly by long beams, possibly less stiff than needed. Hoping to make settings easier and more stable, I suggest: Individual movements for the dampers hold at a fixed beam; Individual springs to push each damper against a string course; One common action on each side, moved by the pedal, to pull all dampers from the strings; Optionally, the contact between the action and the dampers can be adjusted individually. The dampers for the central portions of treble strings still need some transmission. I wish the strings would sound for longer with the dampers. Enabling fine adjustments must help. ========== The medium alternates long string courses with others split in two by a bridge (bridges have voids for the uninterrupted strings). Angles by the bridges put courses higher at one end or the other to help the musician hit the desired note. If no bridge shortened these longer courses, an identical ratio between the full length, the longer part and the shorter part would be the golden number, (1+sqrt(5))/2 ~ 1.618. At identical sound speed in the strings, the intervals would be 8 or better 9 semitones (minor or major sixth) between full length, long part and short part, so 2*9 courses would span 27 semitones at uniform sound speed. The bridge loses about 2 semitones. That's still 4 semitones more than presently, with notes arranged more logically and with uniform sound speed. Whether this is advantageous, and enough so to learn a new string chart? ========== Why 4 strings per note? For a strong attack but longer sustain at medium and treble notes, 2 strings offer eigenmodes with no net force on the bridge and soundboard, and 3 strings suppress the roll moments too. 4 bring no further advantage here, and the piano has only 3. String inharmonicity improves with finer strings, and then more strings keep some moving mass. Though, I believe inharmonicity has been hugely overstated; it's not even a drawback with reasonable diameters like here. Maybe 4 strings cost less than 3. They replace a time-consuming knot on the instrument's left by a turn, plus one cheap tuning peg and its hole at the right. Pianos share some wires before and beyond the turn among adjacent notes, but their tension is very nearly the same, as opposed to the cimbalom. I suppose there is some design flexibility here. ========== Existing instruments widen very slowly at the low notes. Did Schunda consider his design already bulky and heavy enough? Consequently, the nearer strings are far too short, see the drawing: the farther medium strings are healthy 1.23*C or even 1.35*C long (as compared to the sound speed in air) but the nearer medium strings drop to 1.03*C or 0.83*C, and the nearer bass strings to meager 0.37*C, usually a receipe for bad sound. Small cimbaloms widen much more strongly at the nearer strings. Would it hamper playing the big instruments? At least, longer near strings would keep a decent sound speed. The farther medium strings could keep their length and the nearer be 1.3* as long. With the present notes chart, the nearer medium strings would be 1.08*C and 1.32*C long, perfect for plain steel strings and for the transition to spun bass strings. If keeping straight bridges, the lowest bass string would be 1.63* longer, or more decent 0.60*C. Drawing later and maybe. The instrument then widens from 1.5m to 2.1m. Many cimbaloms still have a wooden frame. I hope a metal frame would stabilize the tuning and let the instrument weigh less than Schunda's 1870 design, 100kg. Later and maybe. ========== The angles in the strings hamper the movements of the bridges and put also much pressure on the soundboard, which must be sturdy and is even supported by pillars under the bridges. Efficient reasons for the lack of sonority. Zig-zags at the bridge, like at the piano, would solve all. They are not possible at the highest strings. Elsewhere, they need an instrument higher at the sides, which a metal frame should enable. Later and maybe. Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
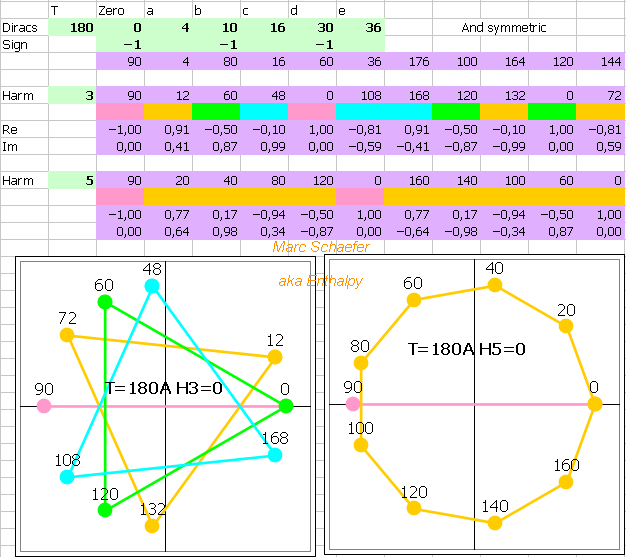
Algebraic proof that H5=H7=0 for the waveform with H3=-135dBc, having 35 transitions and T=210, here on June 01, 2019 Waveform ----------------------------------------------------------------------------------------- Dirac sign | - + - + - + - + - + - + - + - + - + Positions | 0 5 6 9 12 14 17 25 27 31 33 36 37 42 43 50 51 52 | -5 -6 -9 -12 -14 -17 -25 -27 -31 -33 -36 -37 -42 -43 -50 -51 -52 ----------------------------------------------------------------------------------------- Harmonic 5 ----------------------------------------------------------------------------------------- Modulo T/5=42 | 0 5 6 9 12 14 17 25 27 31 33 36 37 0 1 8 9 10 | 37 36 33 30 28 25 17 15 11 9 6 5 0 41 34 33 32 ----------------------------------------------------------------------------------------- +21 if -Dirac | 21 5 27 9 33 14 38 25 6 31 12 36 16 0 22 8 30 10 | 37 15 33 9 28 4 17 36 11 30 6 26 0 20 34 12 32 ----------------------------------------------------------------------------------------- Ordered | 0 0 4 5 6 6 8 9 9 10 11 12 12 14 15 16 17 20 | 21 22 25 26 27 28 30 30 31 32 33 33 34 36 36 37 38 ----------------------------------------------------------------------------------------- Cycles | (0 14 28) (6 20 34) (8 22 36) | (0 21) (4 25) (5 26) (6 27) (9 30) | (9 30) (10 31) (11 32) (12 33) (12 33) | (15 36) (16 37) (17 38) ----------------------------------------------------------------------------------------- Harmonic 7 ----------------------------------------------------------------------------------------- Modulo T/7=30 | 0 5 6 9 12 14 17 25 27 1 3 6 7 12 13 20 21 22 | 25 24 21 18 16 13 5 3 29 27 24 23 18 17 10 9 8 ----------------------------------------------------------------------------------------- +15 if -Dirac | 15 5 21 9 27 14 2 25 12 1 18 6 22 12 28 20 6 22 | 25 9 21 3 16 28 5 18 29 12 24 8 18 2 10 24 8 ----------------------------------------------------------------------------------------- Ordered | 1 2 2 3 5 5 6 6 8 8 9 9 10 12 12 12 14 15 | 16 18 18 18 20 21 21 22 22 24 24 25 25 27 28 28 29 ----------------------------------------------------------------------------------------- Cycles | (2 12 22) (2 12 22) (5 15 25) | (8 18 28) (8 18 28) | (1 16) (3 18) (5 20) (6 21) (6 21) | (9 24) (9 24) (10 25) (12 27) (14 29) ----------------------------------------------------------------------------------------- Marc Schaefer, aka Enthalpy
-
Woodwind Materials
Most woodwind have corks where the joints fit in an other, and corks let woodwind bodies vibrate lengthwise. I take E=G=6MPa and losses=2.2% @1kHz for cork amorimcorkcomposites.com unexpected small losses, but cork does rebound, more so than many elastomers. ========== Let's take a soprano clarinet as an example, with D=14.6mm bore taken as uniform. At the mouthpiece, 1Pa creates 0.17mN axial force. At the fittings, the oscillating air pressure acts on Do~20mm Di=14.6mm to create forces as strong. The bell's flare too experiences axial forces. It the corks are 10mm long and 3mm thick (I have no clarinet at hand), their axial stiffness is 1.3MN/m. This resonates a 20g mouthpiece around 1.2kHz, and together with a 30g barrel at 0.8kHz. The bell resonates somewhat lower, and the driving force can originate elsewhere. If the upper and lower joints weigh 0.15kg each, their fitting resonates them around 0.6kHz. Or rather, these resonances combine. The joints, especially the bell, add their own lengthwise resonances. The frequencies reside at the fundamental's lower clarion to the upper registers, and at the strongest harmonics of the chalumeau register. Bad luck. 1Pa and 0.17mN would move the parts by 0.13nm in quadrature, but Q=45 resonances amplify this to 6nm in-phase. Facings create a lossy pulsation of 10-12m3. Compare with the air column: 1/2* 0.25m D=14.6mm make 21cm3 where 1Pa induce 1.5*10-10m3. A clarinet has Q>100 at these registers, so the lossy pulsation is 1.5*10-12m3. Corks create much losses at a clarinet, according to this model - but experiments decide as usual. It would be worse at an oboe or a bassoon, where the bore is a smaller fraction of the wood section. Q=45 lets affect one note and the neighbour semitones for being so strong. The resonance is too wide to conceal it between two notes, cork is too variable too. Not only is power lost. The blowing resistance is smaller, and the emission of the upper register may become harder. ========== A century ago, woodwinds had impregnated thread coiled on the tenons and bocals. Did it resonate less strongly? I didn't compare when I let install corks at my bassoon, alas. Many elastomers resonate less than cork does. Perfluoroelastomers are an extreme case, they are also hydrophobic and they glide well. Others are easier to glue and cheaper. A limit is that damping materials creep, so the fitting eases over time. ========== Some wooden flutes have silver tenons to connect the joints, for instance Yamaha's YFL-874W and YFL-894W europe.yamaha.com I had suggested that these tenons dampen the flexural resonances, here on Apr 01, 2019 they look also excellent to dampen the lengthwise resonances at the fittings of all wind instruments, since silver absorbs vibrations and is also stiffer than cork: 150MN/m for D=14.6mm e=0.35mm L=10mm. I take a perfectly stiff contact between the metal rings. On metal flutes, the bare accurate adjustment is airtight and slides gently, thanks to thin metal. I suppose that metal tenons in wooden flutes have a location where the diameter doesn't follow the deformations of wood. Maybe ebonite is stable enough that mouthpieces don't need an inner metal lining and the manufacturers don't learn new materials and fabrication methods. But the luthiers and workshops not used to flutes would have to learn adjusting metal rings. Besides (sterling) silver, PCM is a good instrument alloy, and some Ni+Co alloys are known dampers that can be electroformed too: easier for pure oboe or bassoon luthiers. More here on Nov 04, 2018 At a flute B-joint, the fitting is already much shorter than what a clarinet, oboe or bassoon needs. At a conical bore, the fitting must be cylindrical, hence a bit wider that the cone upwards and narrower downwards. Thin metal needs less wood thickness than cork and keeps more sturdy joints. When a clarinettist tunes his instrument down, this creates presently cavities at the air column with deep corrugations. Metal fittings improve this. But the chamber of a saxophone has important functions, so a new design must keep it. Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
35 transitions improve further the waveforms with T=210: -135dBc. H1 H3 H5 H7 H9 H11 H13 | T a b c d e f g h i j k l m n o p q ============================================================================================= 0.52 -126 nil nil -11 -6 -8 | 210 2 7 8 10 12 14 15 16 19 27 28 31 33 40 42 50 51 0.47 -135 nil nil -28 -4 -8 | 210 5 6 9 12 14 17 25 27 31 33 36 37 42 43 50 51 52 ============================================================================================= T=140 and 180 with 35 transitions aren't quite as good as T=210. Neither did 15 transitions provide good waveforms with T<=702, T=840 nor T=1050. Marc Schaefer, aka Enthalpy
-
String Instruments
I suggested to replace spruce or sycamore with yew (Taxus baccata), here on February 10, 2019 12:33 AM, to increase the flexibility of the midrib of traditional harps while keeping the resistance. This applies to much of the harp's soundboard too. Wherever the strings' tension makes the soundboard too stiff, yew will be more flexible and louder. It would apply to any instrument whose strings tension limits the soundboard. How does yew sound in a harp? This must be experimented. Yew was sought after for mandolins, not only for long bows. The definitive way to build loud harps should be my soundboards parallel to the strings, which don't suffer the same limitations hence shouldn't benefit from yew. Marc Schaefer, aka Enthalpy
-
Electric helicopter
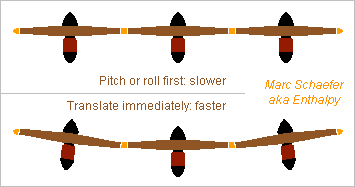
Multirotors use to have all rotors in the same plane. To translate longitudinally or sidewise, they must first pitch or roll, which takes time. The reaction time matters if flying in the wind near a moutain slope for instance, or near a building... I propose to tilt some or all rotors inwards, both length and sidewise. Increased thrust at some rotors and decreased at the opposite ones then creates immediately a net in-plane thrust and acceleration, even before the pitch or roll builds up. The tilt sketched here wastes 1% of the lift force for each tilt direction. Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
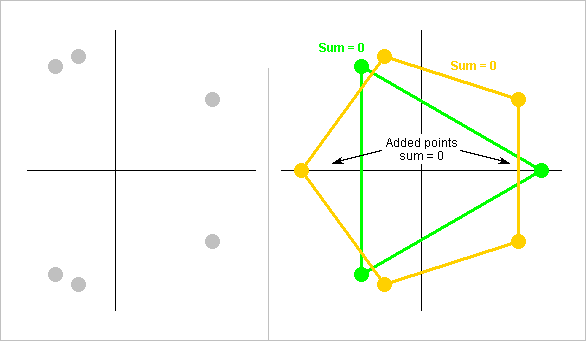
I suggested to add virtual points to a constellation to prove its sum is zero May 05, 2019 12:50 am It hasn't been necessary up to now, so here's an artificial case to illustrate it.
-
Quasi Sine Generator
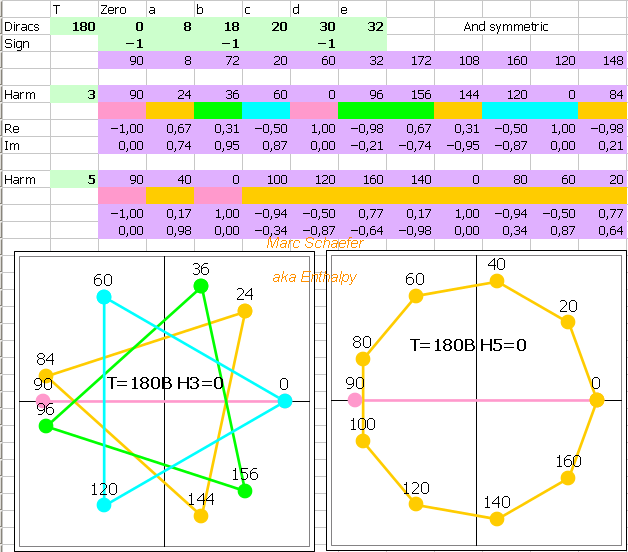
Algebraic proof that H5=H7=0 for the waveform with H3=-124dBc, having 33 transitions and T=210, from May 13, 2019 here Waveform ------------------------------------------------------------------------------------- Dirac sign | + - + - + - + - + - + - + - + - + Positions | 0 3 4 9 10 12 14 16 20 21 23 36 41 42 43 50 51 | -3 -4 -9 -10 -12 -14 -16 -20 -21 -23 -36 -41 -42 -43 -50 -51 ------------------------------------------------------------------------------------- Harmonic 5 ------------------------------------------------------------------------------------- Modulo T/5=42 | 0 3 4 9 10 12 14 16 20 21 23 36 41 0 1 8 9 | 39 38 33 32 30 28 26 22 21 19 6 1 0 41 34 33 ------------------------------------------------------------------------------------- +21 if -Dirac | 0 24 4 30 10 33 14 37 20 0 23 15 41 21 1 29 9 | 18 38 12 32 9 28 5 22 0 19 27 1 21 41 13 33 ------------------------------------------------------------------------------------- Ordered | 0 0 0 1 1 4 5 9 9 10 12 13 14 15 18 19 20 | 21 21 22 23 24 27 28 29 30 32 33 33 37 38 41 41 ------------------------------------------------------------------------------------- Cycles | (0 14 28) (1 15 29) (4 18 32) (5 19 33) | (9 23 37) (10 24 38) (13 27 41) | (0 21) (0 21) (1 22) (9 30) (12 33) (20 41) ------------------------------------------------------------------------------------- Harmonic 7 ------------------------------------------------------------------------------------- Modulo T/7=30 | 0 3 4 9 10 12 14 16 20 21 23 6 11 12 13 20 21 | 27 26 21 20 18 16 14 10 9 7 24 19 18 17 10 9 ------------------------------------------------------------------------------------- +15 if -Dirac | 0 18 4 24 10 27 14 1 20 6 23 21 11 27 13 5 21 | 12 26 6 20 3 16 29 10 24 7 9 19 3 17 25 9 ------------------------------------------------------------------------------------- Ordered | 0 1 3 3 4 5 6 6 7 9 9 10 10 11 12 13 14 | 16 17 18 19 20 20 21 21 23 24 24 25 26 27 27 29 ------------------------------------------------------------------------------------- Cycles | (0 10 20) (3 13 23) (7 17 27) | (1 16) (3 18) (4 19) (5 20) (6 21) (6 21) | (9 24) (9 24) (10 25) (11 26) (12 27) (14 29) ------------------------------------------------------------------------------------- Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
33 transitions improve the waveforms with T=210. T=180 stays bad. The reduction in H3 to -124dBc is compatible with luck and a uniform distribution of the harmonic voltage amplitude. The many trials result from minor optimizations, overclocking, and patience. H1 H3 H5 H7 H9 H11 | T a b c d e f g h i j k l m n o p ==================================================================================== 0.48 -115 nil nil -10 -23 | 210 1 2 7 10 11 12 14 15 20 24 35 38 45 46 47 48 0.35 -124 nil nil +4 -12 | 210 3 4 9 10 12 14 16 20 21 23 36 41 42 43 50 51 ==================================================================================== An different attempt up to T=554 and at T=630 with 15 transitions was sterile. Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
Algebraic proof that H5=H7=0 for some long waveforms listed on May 05, 2019 06:35 pm Since T=210 divides by 5 and 7, I don't multiply the Diracs' positions by 5 or 7 any more; instead, I keep them but compute modulo 42 or 30 respectively. ---------- Waveform (210, 2, 7, 14, 16, 19, 20, 26, 28, 42, 43) Waveform ------------------------------------------------------------- Dirac sign | + - + - + - + - + - + Positions | 0 2 7 14 16 19 20 26 28 42 43 | -2 -7 -14 -16 -19 -20 -26 -28 -42 -43 ------------------------------------------------------------- Harmonic 5 ------------------------------------------------------------- Modulo T/5=42 | 0 2 7 14 16 19 20 26 28 0 1 | 40 35 28 26 23 22 16 14 0 41 ------------------------------------------------------------- +21 if -Dirac | 0 23 7 35 16 40 20 5 28 21 1 | 19 35 7 26 2 22 37 14 21 41 ------------------------------------------------------------- Ordered | 0 1 2 5 7 7 14 16 19 20 21 | 21 22 23 26 28 35 35 37 40 41 ------------------------------------------------------------- Cycles | (0 7 14 21 28 35) (7 21 35) | (1 22) (2 23) (5 26) | (16 37) (19 40) (20 41) ------------------------------------------------------------- Harmonic 7 ------------------------------------------------------------- Modulo T/7=30 | 0 2 7 14 16 19 20 26 28 12 13 | 28 23 16 14 11 10 4 2 18 17 ------------------------------------------------------------- +15 if -Dirac | 0 17 7 29 16 4 20 11 28 27 13 | 13 23 1 14 26 10 19 2 3 17 ------------------------------------------------------------- Ordered | 0 1 2 3 4 7 10 11 13 13 14 | 16 17 17 19 20 23 26 27 28 29 ------------------------------------------------------------- Cycles | (0 10 20) (3 13 23) (7 17 27) | (1 16) (2 17) (4 19) | (11 26) (13 28) (14 29) ------------------------------------------------------------- ---------- Waveform (210, 1, 2, 4, 6, 10, 19, 25, 34, 35, 39, 41, 43, 46) Waveform ------------------------------------------------------------------------- Dirac sign | - + - + - + - + - + - + - + Positions | 0 1 2 4 6 10 19 25 34 35 39 41 43 46 | -1 -2 -4 -6 -10 -19 -25 -34 -35 -39 -41 -43 -46 ------------------------------------------------------------------------- Harmonic 5 ------------------------------------------------------------------------- Modulo T/5=42 | 0 1 2 4 6 10 19 25 34 35 39 41 1 4 | 41 40 38 36 32 23 17 8 7 3 1 41 38 ------------------------------------------------------------------------- +21 if -Dirac | 21 1 23 4 27 10 40 25 13 35 18 41 22 4 | 41 19 38 15 32 2 17 29 7 24 1 20 38 ------------------------------------------------------------------------- Ordered | 1 1 2 4 4 7 10 13 15 17 18 19 20 21 | 22 23 24 25 27 29 32 35 38 38 40 41 41 ------------------------------------------------------------------------- Cycles | (1 15 29) (4 18 32) (7 21 35) | (10 24 38) (13 27 41) | (1 22) (2 23) (4 25) | (17 38) (19 40) (20 41) ------------------------------------------------------------------------- Harmonic 7 ------------------------------------------------------------------------- Modulo T/7=30 | 0 1 2 4 6 10 19 25 4 5 9 11 13 16 | 29 28 26 24 20 11 5 26 25 21 19 17 14 ------------------------------------------------------------------------- +15 if -Dirac | 15 1 17 4 21 10 4 25 19 5 24 11 28 16 | 29 13 26 9 20 26 5 11 25 6 19 2 14 ------------------------------------------------------------------------- Ordered | 1 2 4 4 5 5 6 9 10 11 11 13 14 15 | 16 17 19 19 20 21 24 25 25 26 26 28 29 ------------------------------------------------------------------------- Cycles | (1 6 11 16 21 26) (4 9 14 19 24 29) | (5 15 25) | (2 17) (4 19) (5 20) | (10 25) (11 26) (13 28) ------------------------------------------------------------------------- ---------- Waveform (210, 3, 4, 5, 6, 11, 14, 15, 17, 26, 27, 29, 31, 43, 45) Waveform ----------------------------------------------------------------------------- Dirac sign | + - + - + - + - + - + - + - + Positions | 0 3 4 5 6 11 14 15 17 26 27 29 31 43 45 | -3 -4 -5 -6 -11 -14 -15 -17 -26 -27 -29 -31 -43 -45 ----------------------------------------------------------------------------- Harmonic 5 ----------------------------------------------------------------------------- Modulo T/5=42 | 0 3 4 5 6 11 14 15 17 26 27 29 31 1 3 | 39 38 37 36 31 28 27 25 16 15 13 11 41 39 ----------------------------------------------------------------------------- +21 if -Dirac | 0 24 4 26 6 32 14 36 17 5 27 8 31 22 3 | 18 38 16 36 10 28 6 25 37 15 34 11 20 39 ----------------------------------------------------------------------------- Ordered | 0 3 4 5 6 6 8 10 11 14 15 16 17 18 20 | 22 24 25 26 27 28 31 32 34 36 36 37 38 39 ----------------------------------------------------------------------------- Cycles | (3 10 17 24 31 38) (4 11 18 25 32 39) | (0 14 28) (6 20 34) (8 22 36) | (5 26) (6 27) (15 36) (16 37) ----------------------------------------------------------------------------- Harmonic 7 ----------------------------------------------------------------------------- Modulo T/7=30 | 0 3 4 5 6 11 14 15 17 26 27 29 1 13 15 | 27 26 25 24 19 16 15 13 4 3 1 29 17 15 ----------------------------------------------------------------------------- +15 if -Dirac | 0 18 4 20 6 26 14 0 17 11 27 14 1 28 15 | 12 26 10 24 4 16 0 13 19 3 16 29 2 15 ----------------------------------------------------------------------------- Ordered | 0 0 0 1 2 3 4 4 6 10 11 12 13 14 14 | 15 15 16 16 17 18 19 20 24 26 26 27 28 29 ----------------------------------------------------------------------------- Cycles | (0 10 20) (4 14 24) (6 16 26) | (0 15) (0 15) (1 16) (2 17) (3 18) | (4 19) (11 26) (12 27) (13 28) (14 29) ----------------------------------------------------------------------------- ---------- Waveform (210, 2, 9, 18, 21, 22, 24, 28, 30, 32, 33, 38, 40, 43, 45, 51) Waveform --------------------------------------------------------------------------------- Dirac sign | - + - + - + - + - + - + - + - + Positions | 0 2 9 18 21 22 24 28 30 32 33 38 40 43 45 51 | -2 -9 -18 -21 -22 -24 -28 -30 -32 -33 -38 -40 -43 -45 -51 --------------------------------------------------------------------------------- Harmonic 5 --------------------------------------------------------------------------------- Modulo T/5=42 | 0 2 9 18 21 22 24 28 30 32 33 38 40 1 3 9 | 40 33 24 21 20 18 14 12 10 9 4 2 41 39 33 --------------------------------------------------------------------------------- +21 if -Dirac | 21 2 30 18 0 22 3 28 9 32 12 38 19 1 24 9 | 40 12 24 0 20 39 14 33 10 30 4 23 41 18 33 --------------------------------------------------------------------------------- Ordered | 0 0 1 2 3 4 9 9 10 12 12 14 18 18 19 20 | 21 22 23 24 24 28 30 30 32 33 33 38 39 40 41 --------------------------------------------------------------------------------- Cycles | (0 14 28) (4 18 32) (10 24 38) | (0 21) (1 22) (2 23) (3 24) (9 30) (9 30) | (12 33) (12 33) (18 39) (19 40) (20 41) --------------------------------------------------------------------------------- Harmonic 7 --------------------------------------------------------------------------------- Modulo T/7=30 | 0 2 9 18 21 22 24 28 0 2 3 8 10 13 15 21 | 28 21 12 9 8 6 2 0 28 27 22 20 17 15 9 --------------------------------------------------------------------------------- +15 if -Dirac | 15 2 24 18 6 22 9 28 15 2 18 8 25 13 0 21 | 28 6 12 24 8 21 2 15 28 12 22 5 17 0 9 --------------------------------------------------------------------------------- Ordered | 0 0 2 2 2 5 6 6 8 8 9 9 12 12 13 15 | 15 15 17 18 18 21 21 22 22 24 24 25 28 28 28 --------------------------------------------------------------------------------- Cycles | (2 12 22) (2 12 22) (5 15 25) (8 18 28) (8 18 28) | (0 15) (0 15) (2 17) (6 21) | (6 21) (9 24) (9 24) (13 28) --------------------------------------------------------------------------------- Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
Here's an algebraic proof that H3=H5=0 for the waveform (210, 3, 10, 15, 30, 32) of Jan 21, 2018 9:58 pm updated May 07, 2019 ------------------------------------------------------------------------- Dirac sign | + - + - + - + - + - + Positions | [ -32 -30 -15 -10 -3 0 ] 3 10 15 30 32 ------------------------------------------------------------------------- *3, +T/2 if - | 114 15 165 75 201 105 9 135 45 195 96 Increasing | 9 15 45 75 96 105 114 135 165 195 201 Cycles | (15 45 75 105 135 165 195) (96 201) (9 114) ------------------------------------------------------------------------- *5, +T/2 if - | 50 165 135 55 195 105 15 155 75 45 160 Increasing | 15 45 50 55 75 105 135 155 160 165 195 Cycles | (15 45 75 105 135 165 195) (50 155) (55 160) ------------------------------------------------------------------------- First cycles with 7 members. Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
T was twice longer than needed on Jan 21, 2018 9:58 pm T=90 and T=210 allow H3=H5=0, so here's an aggiornamento: H1 H3 H5 H7 H9 H11 | T a b c d e ==================================================== 0.42 nil nil -2 2 -3 | 90 2 5 8 15 18 0.71 nil nil -9 -11 -3 | 90 4 9 10 15 16 0.79 nil nil -20 nil 1 | 210 3 10 15 30 32 ==================================================== H3=0 for the first time with T=210. More harmonics show that the second waveform outperforms the first one. The third suggests two matched resistors to squeeze H7. (210, 5, 14, 16) suggested already two matched resistors to squeeze H3 and H9 at once. Mar 04, 2018 9:05 pm
-
Quasi Sine Generator
Detail improvement let my dumb program Search2931357.zip find T=210 waveforms with 29 and 31 transitions per half-period. They increase the H1 amplitude or squeeze the H3 further, as compared with the waveforms of Mar 03, 2018 that make the top of the table here. H1 H3 H5 H7 H9 | T a b c d e f g h i j k l m n o ============================================================================ 0.73 -104 nil nil -23 | 210 2 7 14 16 19 20 26 28 42 43 0.34 -114 nil nil 6 | 210 3 6 7 14 22 35 36 38 43 45 46 0.59 -111 nil nil -19 | 210 5 6 10 14 16 17 19 20 29 32 44 46 0.38 -114 nil nil -8 | 210 1 2 4 6 10 19 25 34 35 39 41 43 46 ============================================================================ 0.61 -111 nil nil -19 | 210 3 4 5 6 11 14 15 17 26 27 29 31 43 45 0.42 -115 nil nil -9 | 210 1 2 4 9 16 19 24 26 29 31 35 36 41 43 51 0.30 -116 nil nil -6 | 210 2 9 18 21 22 24 28 30 32 33 38 40 43 45 51 ============================================================================ T=180 is bad but here T=210 improves a bit. Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
I forgot to explain in the last message that, when a Dirac is negative in the convolving sequence, and has the position p after multiplication by the harmonic rank, I replace it with a positive one at position T/2-p or T/2+p. The effect on the harmonic's amplitude is the same. Diracs all positive can then be grouped just by their spacings. ========== Here's a algebraic proof that H5=H7=0 in the (210, 5, 14, 16) sequence I proposed and depicted on Mar 04, 2018 9:05 pm and Mar 17, 2018 8:33 pm I multiply the positions by 5 respectively 7, replace the negative Diracs positions p by positive ones at T/2-p, compute modulo T=210, and sort by increasing positions: ================================ + - + - + - + H1 -16 -14 -5 0 5 14 16 ================================ H5 130 175 185 105 25 35 80 25 35 80 105 130 175 185 ================================ H7 98 203 175 105 35 7 112 7 35 98 105 112 175 203 ================================ Then I group the Diracs: H5 (25 130) (80 185) (35 105 175) H7 (7 112) (98 203) (35 105 175) The pairs are T/2=105 ticks apart, the triplets T/3=70, so the sums are zero. This very short sequence was manageable by looking at the numbers. The previous (180, 4, 10, 16, 30, 36) needed drawings. Sequences with 27 transitions need some better help. ========== The proofs explain why highly composite sequence lengths like 180 or 210 favour the suppression harmonics. They don't explain why the rank of a suppressed harmonic divides the length of the found sequences. Was it a coincidence? Marc Schaefer, aka Enthalpy
-
Quasi Sine Generator
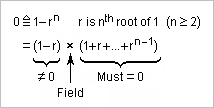
Here's eventually an algebraic proof that H3=H5=0 for both T=180 sequences with 11 transitions scienceforums on Jan 21, 2018 9:58 pm Of the convolving sequence explained there scienceforums on Jan 13, 2018 6:38 pm I represent the complex amplitude of a given harmonic, H3 or H5, at each position of a Dirac, including the ones before zero. These amplitudes are also the contributions of each Dirac to said harmonic, by Fourier series. The angles are computed modulo one turn, that is 180 ticks here. Then, I use the known property that in a (commutative?) field, here the complex numbers, the sum of the powers of a root of 1 is zero. On the diagrams above, I use n=3 and n=9. n=2 too if you decide that sqrt(1)=-1, or rather use 1-1=0. The 3rd and 9th roots of 1 are exp(j*2pi/3) and exp(j*2pi/9) in the complex plane. Any set of points regularly spaced on the unit circle has a null sum, including if all are multiplied by the same amount exp(j*angle). The positions of the Diracs in the sequance are multiplied by the harmonic's order, modulo one turn. I could decompose the constellations into sums of 2, 3 or 9 points regularly spaced. The set of 9 could also be 3 sets of 3. Spacing is 20, 60 and 90 ticks here, for 180 ticks per period, displayed as 40°, 120° and 180°. Note that these sequences occupy the point 1 twice. Because the convolving sequence is even, the imaginary part of all harmonics' amplitude is zero. Interesting is the real part of the sums. Conjugating some points may help to form regularly spaced sets. Here it wasn't necessary. Adding to a constellation virtual points whose sum is zero may help form several regularly spaced sets. Here it wasn't necessary. I ignore if all good convolving sequences must be constructed that way, and leave this question to a mathematician. Software searching only convolving sequences constructed that way may be faster than what I did, but programming is not trivial. Here is the spreadsheet. The original xml is for Gnumeric, the exported xls for Excel loses some formatting. ProofT180abH3H5.zip Marc Schaefer, aka Enthalpy
-
Electric helicopter
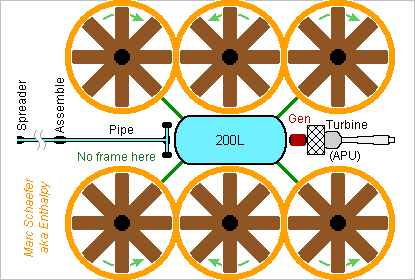
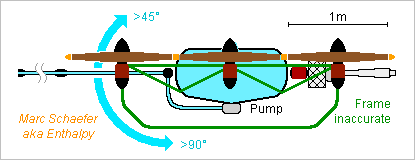
This quadcopter or, for redundancy, hexacopter shall extinguish fires, optionally in cities too. The multirotor is simpler and cheaper than a helicopter, and easier to (help) pilot by software. Its rotors are easier to surround by protective stators. It adds advantages specific to firefighters: The pipe and jet can aim up and down between the rotors, if no frame element interrupts the movement there, to tackle the braze from the side instead of fanning it. This lets tank in flight from a river, a fountain... with a reversible pump or two pumps. The tank is accessible from the top and the bottom. The jet creates a smaller torque and the rotors compensate it better. Mass estimate: -------------- 6*5kg Rotors with electric motors 30kg Gas turbine and generator, 70kW 3kg Empty tank 10kg Frame 10kg Pump 8kg Pipe 2kg Electronics 7kg Undetailed 200kg Water -------------- 100kg Empty 300kg Full Six D=1m rotors accelerate together 131kg/s air from 0 to 23m/s to hover. At 70% efficiency, this needs 50kW, but climbing at 7m/s takes 70kW, and hovering with a defect rotor needs power too. Batteries don't suffice here, a piston engine would reduce the payload. A fuel cell does the job but hydrogen may awake superstitions. A gas turbine is light, possibly from a small APU. Get inspiration there http://www.scienceforums.net/topic/73798-quick-electric-machines/?do=findComment&comment=737931 for the gearless light generator and for the geared motors. The pump isn't easy. 60% efficiency need 3.3kW for 2 bar and 200L in 20s. A centrifugal design is compact and the motor too, but it sucks water badly when air is in the pipe. Maybe a fast screw pump https://www.scienceforums.net/topic/73571-rocket-engine-with-electric-pumps/?do=findComment&comment=734835 or a second centrifugal pump at the lower end of an optionally separate pipe. Have floats under the frame? The pipe is preferably of graphite composite, possibly a sandwich. Metal would need intricate reinforcements. Software would usefully stabilize it against the frame's pitch. The sketches and figures let the copter fit in a lorry. 2-4 people carry it empty. It can still manoeuvre in Parisian streets, and possibly arrive by flight from the fire station. Scaling up and down is possible. Marc Schaefer, aka Enthalpy
-
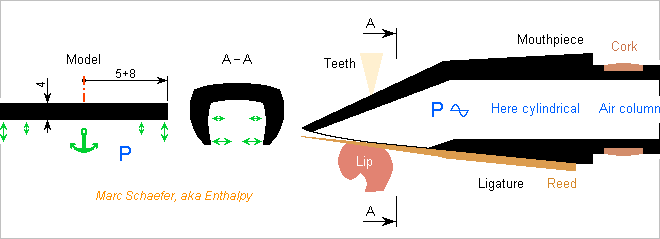
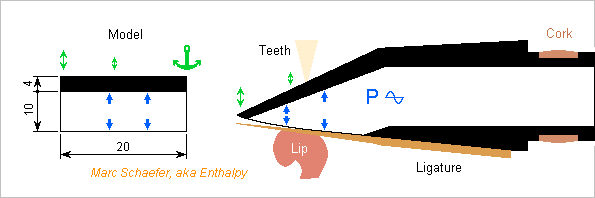
Woodwind Materials
Tone holes let a woodwind body vibrate as they break the symmetry, so are there vibrations at the mouthpiece of a single-reed instrument? Let E=2.5GPa and rho=1400kg/m3 for ebonite. The dimensions are from a soprano clarinet. ========== Where the bore meets the reed, the mouthpiece section is open hence more flexible, and the sides may vibrate laterally. For hand computation, I model the U shape as a flat part hold at the middle, 4mm thick, 2*13mm wide. Per metre length, EI=13 and µ=5.6. The first flexural resonance, with k*13mm~pi/2, occurs around 3.6kHz. The fundamental of a soprano clarinet doesn't reach this frequency. Amateurs are expected to reach written G an octave above treble clef, so the resonance would be the H3 of a high note. For professionals who reach higher notes, it could also be H2. Resonance would affect the emission of a note and its timbre, as we hear these frequencies well. How much? Static 1Pa would deform the tips by 0.27nm, creating a displacement of 9*10-15m3. For comparison, a D=14.6mm L=0.4m air column (*0.5, the mean value of cos2) contains 33cm3, which 1Pa compress by 2.4*10-10m3, so the mouthpiece's lateral deformation is 26000* smaller. Now, ebonite may resonate with Q=40, so the deformation is 650* smaller and its phase dissipative. Accounting ideal bore friction, conduction and radiation for a clarinet at 3.6kHz, but not the losses at the tone holes, Q~50, which the /650 deformation reduces to 46. The effect is small. But if ebonite had been half as thick, the effect 8* worse and at a note's fundamental would have been annoying. Once again, existing designs are good but don't take huge margins. Metal puts stronger resonances at higher frequencies, which should make no difference here. It's more a matter of accurate manufacturing, thermal comfort, condensation. Polyketone with E=1.3GPa would need a bit more thickness, while liquid crystal polymer with E=9GPa could accept less. Ease of manufacturing can decide. ========== Pressure oscillations act vertically on the mouthpiece, stronger than at tone holes, and the opposite force on the reed acts only at the ligature, but the mouthpiece's tip vibrates little thanks to its stiffness. I make a very coarse model with thickness constant over the length. The first resonance is then around 7kHz and the displaced volume 5* smaller than for the sides lateral vibrations. Nothing to worry about. ========== The reed and mouthpiece end transmit strong vibrations downstream, possibly to the instrument's body. The big area at a pressure antinode has more potential than the closed tone holes effect described here on Nov 13 and 26, 2017. If the musician didn't apply his teeth and lip, the opposite pressure forces on the mouthpiece and reed would compensate at the ligature, because the reed resonates at a frequency exceeding much the sound, so its inertia is negligible and the reed transmits all the force over the ligature. The stiff teeth and skull reduce the mouthpiece's force, the softer lip at the reed's strong movement too. How much of each remains is impossible to evaluate from my armchair, sorry for that, but they won't compensate an other. The skilled musician reduces the reed's vibration amplitude with his lip consistency to obtain a mellow sound, so much of the force is absorbed. The cork isolates strongly the barrel or bocal from the mouthpiece's vibrations. A tenon of absorbing material like silver would be stiffer and damp the resonances too. Some mouthpieces have a softer insert for the teeth. It limits the transmission to the skull and internal ears, but may also damp the mouthpiece's movements. This, together with the mouthpiece's mass, could make a difference to the listener, more so at low instruments. Marc Schaefer, aka Enthalpy
-
String Instruments
Can Japanese string instruments replace ivory by sustainable materials? The koto has big bridges and small plectrums, the shamisen a bridge and a big plectrum, of ivory bbc.com as do more instruments, outside Japan too. Ivory is difficult to replace, data from Marie Albéric' thesis: tel.archives-ouvertes.fr page 47 Ivory POM-CF LCP LCP-CF ------------------------------------------------------------ Density 1700 1470 1400 1500 kg/m3 Young 12 10.4 9.1 26 GPa flex Resistance 320 170 158 228 MPa flex Damping ? ? 0.06 0.03 Friction ? ? ? ? On string ------------------------------------------------------------ I suppose, but haven't computed, that bridges don't load the material to the limit. The replacement should mimic ivory's density and stiffness, damping too. Ceramics would be too stiff and traditional polymers, here POM-CF, not enough. Liquid crystal polymer (LCP) becomes too stiff with 30% graphite choppers, so less choppers would adjust Young's modulus. Some heavy filler can increase the density. Or would glass choppers achieve both at once and keep the bulk colour? At plectrums, the flexibility of ivory seems impossible to imitate by the material alone. 2.7% flexural strain at break are inaccessible to metals, ceramics, nor the polymers listed here. Other fibres may, especially meta-aramide, with high damping then, and they need a matrix with big flexural strain, but has their composite the necessary stiffness and resistance? Orienting long fibers can help. Stretching LCP during the extrusion or injection too, as this hardens it much. Adjusting the shape softens plectrums, bridges too if they have shallow stressed parts. 26GPa against 12GPa allow parts equally stiff 1.47* thinner and broader at same volume and slightly more at same mass, not enough. But I hope plectrums can be marginally heavier. If the shamisen's plectrum stays wide towards the handle instead of narrowing linearly, unloaded LCP 1.54* thinner and 4.80* wider has the same fexibility and strength as ivory - flexibility alongside the string if needed to soften the sound would be more difficult, with radial grooves. If the koto's plectrum isn't curved like a nail but flat near the finger, and wider or possibly a bit thicker, it gets flexible too if needed. Maybe. Marc Schaefer, aka Enthalpy
-
Woodwind Materials
Some wooden flutes have silver tenons to connect the joints, for instance Yamaha's YFL-874W and YFL-894W europe.yamaha.com which reduces the risk of cracking and saves the extra wood thickness to accommodate the overlap and the cork. Also, it introduces no deep lossy groove in the air column when tuning the flute down. The manufacturer also claims "adds focus to the sound", "adds tonal body" and the ubiquitous "improved projection", the usual spiel. Or could there be something in it? I proposed here on Oct 30, 2018 that the tone holes couple the air column's vibration with the body's bending modes. Lossy silver tenons dampen the bending resonances. They should act better than cork, which is too soft to dampen stiff wood efficiently. At these places, little silver would have a big effect, including for wood or polymer bodies. If experiments confirm an effect, silver tenons should be generalized wherever they are robust enough. Or cobalt-nickel, copper-manganese and other lossy alloys. Not only at wood, also at polymer and graphite fibre bodies. Beyond flutes, also at oboes, clarinets, of course bassoons, pretty much all woodwinds, brass maybe too. Marc Schaefer, aka Enthalpy
-
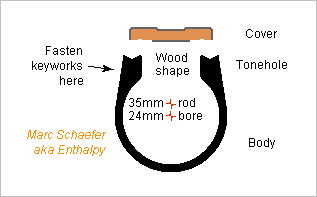
Woodwind Materials
Body material for an alto flute is a difficult choice. D=24mm often, so 0.38mm of 92.5% Ag, with E'=98GPa and rho=10370kg/m3, would bring the elliptic deformation resonance of a full cylinder to 1490Hz, within the alto's range. 0.43mm would reach 1690Hz, a mere semitone above the written C's fundamental, but the harmonics are much higher, and the body resonates lower at the tone holes. The heavier and longer body excludes thick metal for flutists except weightlifters. Yamaha use rose brass for its alto and bass flutes. Interpreted as CuZn15, its E=122GPa E'=139GPa and rho=8750kg/m3 save 16% mass and raise the resonance by 1.30 at the same thickness. At least the elliptic resonance of a full cylinder is a bit above the fundamental range, as on the soprano flute. Though, most flutists prefer silver over copper alloys. Dalbergia wood family seems too heavy. 4mm thick, the naked body would be longer and weigh 2.25* as much as a 3mm soprano, for which many flautists find wood heavy. Big Dalbergia pieces are also difficult to find and fragile. Graphite fibre composites thick enough to save chimneys, as for instance Matit does for soprano flutes, would be too heavy too. ========== Graphite filament winding can bring high resonances and light weight. With isotropic E'=100GPa and rho=1550kg/m3, 2mm are lighter than brass and a plain cylinder resonates at 20kHz. It would require glued chimneys or subtle winding that lays more filaments around the holes. Maybe a polymer loaded with graphite choppers can be decently machined despite being abrasive. Rods of POM-CF and damping ABS-CF are available, polyketone and LCP should outperform them. For ABS-CF, E'>18GPa and rho=1200kg/m3 let a 2mm plain cylinder resonate over 9.9kHz, while the brass mass would allow 3mm composite. The outer profile would be milled after the bore is drilled. A bore centered in the rod just needs a 40mm rod. Extrusion (and reaming) seems possible. The tone holes would be drilled and profiled as in wood. I imagine metal plates glued on the body to hold the keyworks. Flexural modes with ABS-CF would be as fast as with rose brass. LCP-CF would improve a bit. This can inspire other instruments like the clarinet, especially low ones. ========== The other path is a curved body, as suggested here on Mar 22, 2019 on 12:44 AM and 01:23 PM. Marc Schaefer, aka Enthalpy