-
Posts
3887 -
Joined
-
Last visited
-
Days Won
1
Enthalpy last won the day on August 21 2021
Enthalpy had the most liked content!
Recent Profile Visitors
The recent visitors block is disabled and is not being shown to other users.
Enthalpy's Achievements

Scientist (10/13)
252
Reputation
-
Verity2023 started following Enthalpy
-

Misuse? of statistics (was Navigation Ability)
Enthalpy replied to Enthalpy's topic in Other Sciences
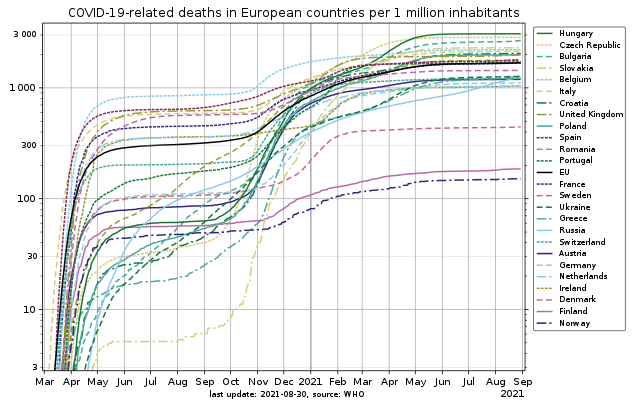
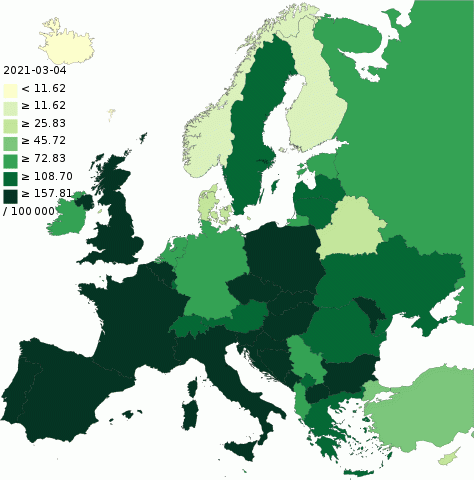
I wrote "Maybe avoiding the contaminations during one wave makes things only worse during a following one" and this graph illustrates it. Notice the log scale. Bigger versions at wikipedia The EU countries less hit after May 2020 (Poland, Czech republic, Slovakia, Hungary and more) caught up or exceeded the others in May 2021. Exceptions are (as of Sep 2021!) Norway, Denmark, Finland. Sweden, with a similar population but without confinement and little social distancing, is more badly hit than Norway and Denmark, but less than the average of the EU. Or maybe time will upset the situation again. Slovakia tested 2/3 of its population in Oct 2020. It's the curve lowest on the graph in Sep 2020. All countries were hit at that time, so the Slovaks didn't get infected at test centres, but the tests didn't bring anything. Governments that make tests mandatory should observe and meditate that curve. A persistent impression: we apply inadequate mental schemes to Covid, which doesn't spread like flu or cold do. Different vectors? Encrypted version while spreading? -
I took two lines to explain one subtraction. The feedback was "what's the connection?" I call that trolling.
- 6 replies
-
-1
-
Don't feed the troll.
-
Hi everyone and everybody, Following the generalized and repeated question about synchrotron radiation wavelength there scienceforums When the deflection is big, at a star, at some bending magnets... the beam divergence combined with the angular speed defines the pulse duration, with a known formula. But a horizontally ultrarelativistic particle that falls in a lab experiences an extremely small deflection, so the beam divergence obviously doesn't limit the pulse duration. Instead, the distance over which the particle may emit the observable part of the pulse limits the pulse duration. It should have been clear enough after I related many times the duration with the flight distance: 06 Mar 2016 - 19 Jun 2021 - 22 Aug 2021 It's also the very same and well known computation as in a free electron laser. Example: a photon takes 100ns to fly over 30m, a 7TeV proton is 9.0ppb slower so it takes 0.90fs more than the photon, and for an observer close to the proton flight path, the end of the pulse (emitted last) is 0.90fs after start (emitted first), giving a mean period around 1.80fs and mean wavelength around 540nm. I didn't answer, not because the question is tough, but because I claim a physicist should be able to compute a difference, and I felt there were enough indications before. I did answer "what particle" and more questions despite the information was in the first message 10 Jul 2021 but at some point, my patience stretches out. More so when one seems to ask lots of random questions just to swell a thread, derail it, or make it unintelligible, but doesn't invest the minimum time to read it before. Extravagant claims like "strong force and electrostatic repulsion don't contribute to the atomic mass" would take too long to debug in a thread not centred on general understanding of Relativity. Their mix with more advanced jargon produces a deplorable impression - I won't qualify that. And the resurgence by the same person of general understanding questions, or wrong claims, that I had already addressed in other threads, convince me that I would waste my time answering them every time.
-
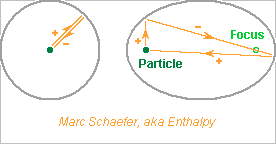
Hi everybody! I wanted to surround a particle beam with a sleeve mirror and coat the inner face of the sleeve mirror with a transparent material to make light as fast as the particle and produce a shorter and stronger light pulse, or a weaker pulse. This dielectric can be thin on a support. But it must be very thin. Take full-energy Pb ions, 57ppb below c at the LHC, divergence +-10mm over 30m. A N=1+0.5 coating in a D=3mm must be 0.34nm thin, just 2-3 atomic layers, and accurate to shorten the pulse. So the first difficulty is to avoid unwanted adsorbed layers. This implies noble materials cleaned under vacuum. Here some reflection coefficients at 2.1eV for pure metals, from the Hdbk of Chem and Phys. Grazing incidence will improve over the normal incidence. Ag 0.94 but oxidises easily Au 0.93 but drops soon with the energy: 0.78 at 2.32eV Al 0.92 but oxidises Rh 0.78 <= Good choice? Pd 0.71 Pt 0.65 Reflection is also distributed in the metal over some depth that changes with the frequency, introducing a group delay. I don't plan to think more at it. ========== A cylindrical sleeve inverts the field sent back to the particle path, so over some length, the emission must be smaller and the synchrotron losses too. An sleeve with elliptic section adds constructively the field emitted at one focus, as it bounces a second time before focussing at the particle path. All paths have also the same transverse length, a synonym for "focus". That seems favourable to the experiment I propose, if light that passed last by one focus can be separated from the other, maybe by a median mirror. Longitudinal focussing (at bending magnets too), accuracy of construction, accuracy of lateral beam position, need more thoughts. I have no plan to do it. Marc Schaefer, aka Enthalpy
-
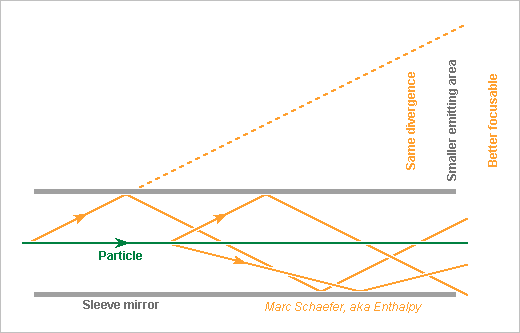
The sleeve mirror suggested on 22 Aug 2021 scienceforums helps to focus the light emitted by the charged particle, as this light exits from a smaller area with a divergence as good. Without sleeve nor other help, light emitted over a huge field depth gives a blurred spot. The mirror must reflect light many times without wasting power. Visible wavelength and grazing incidence help. I imagine only metals, since dichroic layers and metamaterials would spread the half-wave pulse. The mirror lives dangerously around a particle beam, but the diaphragms are narrower and upstream. Near slowly the mirror parts to the stabilized beam according to sensor indications, maybe. The mirror is maybe 1mm away from the beam, but as extreme darkness is needed, checking the Cherenkov emission at distance would be cautious. Marc Schaefer, aka Enthalpy
-
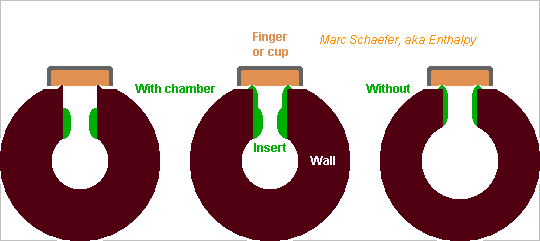
Instruments with sideholes could have inserts there. Or is it already done? Smoothening the hole's inner end, where it meets the air column, is easy at an insert before it is mounted but difficult at the wall alone. scienceforums The hole dimensions adjust the intonation at least at oboes. Replacing the insert chosen in a set is reversible. Some oboes have chambers, I claim their resonances make a mellower sound scienceforums A set of inserts lets adjust the intonation and can keep the resonance unchanged. A protruding ring makes the airtight contact with pads. It wastes scarce wood, needs difficult machining, and wood can split there or lose its flatness. An insert is easier and can use durable polymer (Vectra...) or metal. The inserts are cheaply turned to complex shape. ========== Looks feasible with or without inserts: smoothening the hole's outer end, where it meets the pad, could improve an instrument further, like undercutting does at a clarinet. scienceforums Flutes do it. Pads covered with gut or fish skin and adjusted with paper may help. Marc Schaefer, aka Enthalpy
-
The synchrotron radiation needs a speed very close to c to produce more light than the same acceleration does with little speed. While relativistic effects are easily observed in atoms (electrons deep in heavy atoms have 0.1MeV mean kinetic energy versus 0.5MeV rest mass), the "speed" is still far from c, while protons at the LHC move with (1-9*10-9)c. This makes already a numerical difference. A qualitative difference: "movement" is subtle in QM. Electrons in atoms have a kinetic energy, possibly an orbital momentum, and things you may or not want to call "speed" and "acceleration" because the phase or the amplitude of the wave function changes over the position. But radiation needs in the wavefunction a bulge that moves and accelerates over time, and this is not the case with orbitals, which are "stationary". You can translate this with "immobile" for the sake of light emission. That's how QM explains that atoms in their ground state don't radiate. In a non-stationary state, for instance (2p+1s)/sqrt(2) during a transition, an electron does have a bulged wavefunction that moves at the frequency of the emitted light. The speed isn't favourable, but the number of electrons in a sandwich is (or the number of colour centres in a garnet). My expectation, not fully thought-through, is that the not fantastic speed of the electron in a atom distinguishes it too little from the proton, and that any net emission on a time scale corresponding to the drop duration would be extraordinarily faint. At the LHC, the speed shifts the photon half-period from seconds to femtoseconds and it increases the power too. An operating laser, where electron transitions are synchronous, would be a first improvement. Maybe the fall modulates the emitted light with a faint off-frequency or off-polarisation component. But 240dB had to be found at the LHC to see something despite the huge speed (and not so few protons) so electrons in atoms must be badly discouraging.
-

Cutting / treating glass to refract specific colours ?
Enthalpy replied to Erina's topic in Engineering
Also gratings, and so on. -
Either moving parts in a mechanical sense, or something more costly that redirects light, but that doesn't "move" depending on what one wants to call "move". One more device type to redirect light uses surface acoustic waves. Called "acousto-optic modulator" approximately. An acoustic wave at many MHz creates ripples in a piezo material, these ripples diffract light like gratings do. I expect very low light efficiency. The original query was to redirect light from any direction. That prompted my comment about thermo's second law.
-
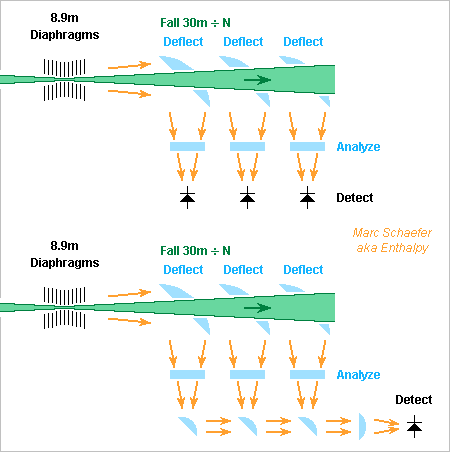
I'm confident now that the path length has no effect on the power emitted by a deflected charge, because light emitted from different positions doesn't add. So the working mental representation is that a detector receives a Dirac pulse from each position of the emitting particle, and the spread of path lengths defines the pulse duration (the pulse shape isn't flat since emission to the sides is weaker) hence the spectrum. ========== My previous message mentions very thin transparent elements around the proton beam. To shorten the pulse to 540nm/2 at the detector, they must delay by 270nm the light emitted by previous section(s), so a material with index N=1+0.5 must be 540nm thin. Maybe semiconductor processes can support such a membrane with a truss of narrow thick fins, possibly with several thickness levels and truss periods. The material would be a bulk transparent one or an oxidized semiconductor, among which nanoporous silica has a low index hence can be thicker. Full-energy protons at the LHC (9*10-9 below c) can fall over 30m to create a 270nm pulse before reaching a retarding membrane, while lead ions (57*10-9) need a membrane every 4.7m. My previous message's sketch lengthens the light path for every section, so only the path difference is so small. I believe membranes here add E rather than P to give a stronger signal. ========== My previous argument about sending information back in time is doubtful, because observing the effect on a proton perturbs it, and all sections may no more add the amplitudes efficiently. Marc Schaefer, aka Enthalpy (I come back)
-
The deflection of protons by gravitation at the LHC is tiny, much smaller than the light cone angle, which doesn't set here the usual pulse duration. So do the usual formulas for emitted power apply, especially in the first message? I believe they do, because among the diverse computations, this one en.wiki obtains a Poynting vector and an emitted power independently of a pulse duration or spectrum. Also: protons at the LHC emit pulses about 1fs long but 0.5A beam intensity puts a proton every <1as, even closer in the bunches. Though, the emitted light cumulates E, not E*H. So why should usual models work, as they cumulate the power from allegedly independent protons? Because only the AC part of the emission propagates, carries power away and is detected as light. For R random protons whose pulses overlap, this fluctuation of E is proportional to sqrt(R) and the power is proportional to R. Signal theory also wants the random sum of independent signals to have the same spectrum as each signal, here light, while the slow deterministic modulation by bunches passes in the light. ========== I had hoped to reduce the synchrotron losses of storage rings by absorbing, diverting, retarding... at many places in a bending magnet the light emitted by one particle by so it doesn't add constructively. This one attempt looks vain presently. What might perhaps work is to reorient the light emitted near the entrance of a bending magnet to inject it near the exit so it adds destructively. An odd number of mirrors should do that. They must need curvature so the injected light mimics the divergence of the fresh one. The path must be inwards over some length so the light catches the particle up. As the particle is delocalized laterally, the reinjection point must follow the delocalisation. Is that feasible, I don't know. At least, synchrotron light is around the visible spectrum at the LHC. Proper interference may need to mirror very short pulses, easier for Pb ions. It needs also subwavelength accuracy over a decametre, as difficult as the VLT. The light of pairs of successive magnets can also cancel out. Light cancelling out means each particle would reaccelerate itself. The width of the particle beam, of the vacuum tube, other dimensions... constrain the design. I didn't even try figures and drawings. A new design may be needed if a retrofit is impossible. Maybe the opposite if feasible too where wanted, increase the emitted light by reinjecting earlier light in phase near the particle. Something reinforces the emitted light at free-electron lasers, I don't know what, maybe that. Or is all that already abandoned? ========== Protons falling at the LHC emit waves a bit too long for quiet detectors. Helium and lead ions are worse. I suggested already to reduce the drop length and accept fewer photons easier to detect, optionally to split the drop length and have several detectors here on 19 Jun 2021 Splitting the drop length in N sections and detectors keeps the light power in /N photons with *N individual energy. Light from individual drop sections could also be sent to a common detector of same area to get more signal with the same noise, as for instance photocathodes are little sensitive to the light's direction: A fascinating option would superpose the pulses of all drop sections at the same time and place to add E rather than P, hence obtain N2 as many photons as from one of these sections. Since light from all sections is coherent, E can add. It looks "only" like a technological challenge similar to the VLT. That would be an other case where hardware downstream influences earlier photon emission, like in EPR experiments. Or is it? At least in principle, the increased photon emission can be noticed from the emitting proton's remaining energy, before the light reaches the influencing optical elements. Acting on these elements would transmit information backwards in time, so my present opinion is that coherent light addition will fail. I carefully neglected to display how light from earlier drop sections passes at later optical elements. The paths can be stacked vertically for instance. But as individual beams arrive at different angles, they may produce an interference pattern that cumulates P over the image, not E. The impossibility might manifest itself as a stubborn technological difficulty to concentrate light within the additive fringe and still transport one light path around the other optical elements, or a difficulty to concentrate the light without spreading the pulse in time. Very thin transparent elements around the proton beam seem impractical. Synchrotron light seems difficult to focus without spreading the pulse over time, since light emitted earlier is broader but arrives earlier. Focussing to a ring could be better than to a spot. A sleeve mirror? Photocathodes can advantageously be big and keep a small dark current. An ironless electromagnet, or the geomagnetic field with removed shield, let emit more photons in the drop region to adjust the optics. ========== More drop segments allow to reduce the energy per nucleon and keep a good wavelength. A smaller gamma reduces identically the gravitation and the magnetic light. Insofar possible, more beam intensity and less energy have advantages: A smaller acceleration at the bending magnets emits less magnetic light, while g stays the same. The same acceleration power makes more gravitation light. The last bending magnet emits light at a longer wavelength, which the diaphragms suppress better. The protons per nucleus may address other limits. Marc Schaefer, aka Enthalpy
-

Misuse? of statistics (was Navigation Ability)
Enthalpy replied to Enthalpy's topic in Other Sciences
Trying to infer logic and means of actions against Covid from statistics is deceiving and disappointing. When Czechs wore makeshift face masks and were spared, I told "Ze big solution". But the next strain of Covid took a horrible toll there, putting the country at once among the worst hit. Poland too was spared but then badly hit by that same strain. Maybe avoiding the contaminations during one wave makes things only worse during a following one. My thoughts are with Australia, that has had little cases but where the more contagious delta variant spreads presently. ========== I still stand behind my old claim, that confinement acted far too late on the incidence in Italy and Spain to be considered a cause. The mean incubation time is allegedly well under two weeks, but strict confinement brought no improvement before a month, if any. The same happened in France in Autumn 2020. But we do see many more cases after mass public gatherings: BLM demonstrations in the USA, Euro soccer championship. Are humans the main vector? Slovakia tested 2/3 of its population in Oct 2020. One can't even see an effect on the curves. I computed and wrote elsewhere "If the contact tracing application worked, it would mark every inhabitant" 20minutes.fr and this started to happen in England. The French expert Didier Raoult, much denigrated for disagreeing with the government, told Waves correspond to virus variants (that's commonplace meanwhile) Masks and confinement bring little or nothing (looks true now, still not widely admitted) Means to treat the patients make the difference (horribly true, compare the countries) Vaccines are not the main solution (still looks wrong). Common vaccines do little or very little against the contamination by the present delta variant, but they still reduce efficiently the number of hospitalisations and deaths. Best example is the UK, where the new cases run as high as in Spring but deaths are cut by /20. This corresponds to the vaccination proportion among people at risk. But if the general population remains as contagious, vaccinating it seems useless. ========== I still try to understand why Sweden, with no confinement and nearly unrestricted public life, went through the pandemic better than the UK, Spain, Italy, France. They had many cases, initially many deaths but not the worst proportion, and since Spring nearly no deaths. The amount of damage is predefined, public policies do nothing? Maybe. Catching earlier strains of Covid disarms the following ones? Everyone got flu previously, this protects against Covid? People who survived flu resist Covid too? Statistics from the USA, South America... tell climate and weather don't matter. Hugo Zeber and Svante Pääbo found an interesting correlation between a gene cluster inherited from Neanderthals and severe symptoms nature.com This seems to hold, and contributes to explain why Sweden is less affected than Southern Europe and pre-Colombian people. An other correlation: the Covid makes less damage in countries where saunas serve regularly, map from Wiki Nordic people would consider that obvious. Though, many Russian died despite saunas since this map. -

Stradivari violin tonal qualities due to....chemicals?
Enthalpy replied to TheVat's topic in Applied Chemistry
If a musician has time to find out the main differences between two bowed instruments, and then plays the instruments for you and tells you at what to listen, you will notice the difference. It's much more striking than between two clarinets. Maybe I should search among the many records on Youtube. I remember hearing a comparison between two celli, it was impressive even over computer loudspeakers. -

Stradivari violin tonal qualities due to....chemicals?
Enthalpy replied to TheVat's topic in Applied Chemistry
Hello nice people! Such theories abound and none uses to be confirmed when checking more samples. Among competing theories, one claims that wood improves over the centuries as it loses mass. Others claimed the wood was stored in ponds for decades. Or that the climate was colder then (but just an altitude 120m higher does the same). As a general warning: mistrust all such claims, especially the spectacular ones. Be they correct or not, they find too easily a path into the general Press to bring career advantages to the authors, especially since the Shanghai rating. For instance "Guarnieri, Guadagnini and Stradivari aren't better" is just cr*p. Violinist do recognize old Italian violins, or rather good instruments. The difference is bigger than for wind instruments. Tests claiming "no difference" are just badly conducted. You notice differences better when playing the instrument than when listening at it. Some affect the ease of playing, not the sound. Musicians hear better than an average journalist. It takes time to notice the differences. I saw a "test" that ran a scale up and down, end. One must target artificially, provoke, check and reproduce the differences. Once you noticed them, you hear them in normal music too. Playing only some Mendelssohn won't tell anything in 5min. But you would notice the differences after days of normal use. Yes, some less old instruments are excellent, equalling arguably old Italian ones. More and more soloists (Hilary Hahn, Vilde Frang...) play instruments made by Vuillaume. One should also remember that the old Italian instruments differ much now from the original sound. The string materials have changed. Huge difference, stronger than between two instruments. The bridge's curvature was increased. To avoid collisions between the bow and the soundbox, bridges rose, and their stronger push relies on thicker bass bars now. This raised some resonances. Finally, many soloists prefer old Italian instruments because these are louder and more brilliant, a necessity to play in a big concert hall with an orchestra accompaniment, but these instruments don't sound nicer at all. Chamber musicians or Gypsies would comment "OK, loud and responds very easily, but sounds horribly, I prefer that other instrument" with a nice warm dark tone.