md65536

Edit: I missed the double-negative and only now see I'm agreeing with you, but I can't find where/if the statement you're quoting was resolved in this thread... How can you one possibly think that it follows, when you can do experiments in the kitchen sink with water and glasses that show that it's complete nonsense? You're Others are forgetting (but it looks like mistermack pointed it out long ago) that the space displaced by the mass that you're floating, does not need to be filled with mercury! So for example, say you have 700 kg of mercury in a container, filled right to the top, and you put in a 600 kg weight and it floats, displacing 600 kg of mercury. This is acceptable, agreed? However, the 600 kg of mercury has spilled over the top, so now you have a 600 kg weight floating on 100 kg of mercury, in the space that can hold 700 kg of mercury. Having tight seals or an "already floating" mass doesn't matter. If you have a stone sitting in a container that is just a little larger than the stone, you can float it using as little mercury as it takes to fill up the space not taken up by the stone.

This demonstrates visual effects of SR by the way, not GR, and is not applicable to this thread. I wasn't paying attention to which topic I was in!

There's http://gamelab.mit.edu/games/a-slower-speed-of-light/ It doesn't have a lot of options but it's built on an open-source Unity toolkit. The description says it shows time dilation (objects should be slower the closer you are to the speed of light) but I don't see it, and I also don't see delay of light (objects should appear faster as you approach them); it might be the effect is too small for me to notice.

Based on context and the forum we're in, the model must be a relativistic one. The quantum argument sounds reasonable but you can't make that claim about a gravitational singularity without a theory of quantum gravity. I don't see how lack of a clear cause is a useful argument. If you use that reasoning, you can claim that spontaneous particle decay can't happen at all. Yes, it seems accepted theory is moving away from the idea of an initial singularity. My limited understanding is that the singularity is considered speculative, shown to be not necessary in some theories, and not possible in others. However the issue isn't settled because to do so would require a theory of quantum gravity. Therefore making claims as if it's settled, is speculation only. I haven't followed OP's arguments, I'm only addressing yours.

Why not? Are you implying that a point particle can't decay?

I think this is the key to understanding it. I also think most people's approach is not best, whereby they imagine a contraption and explain if or how it works. If instead you ask yourself, given that the air is still and the ground is moving at a constant rate relative to it, is it possible to extract usable energy from that? It's obviously "yes". It's obvious that it could be done without breaking the laws of physics. Then other misconceptions easily fall away too. How much energy can be extracted? Now what swansont said is obvious, you would want a bigger propeller to extract more energy (the more you let the ground pull, the more you must push against the air). It's obvious that the moving ground could provide enough energy to overcome friction in a well-engineered device. It's obvious you wouldn't want a weightless vehicle, if you need a downward force against the ground to capture energy from its motion. Then, "How might that energy be turned into thrust, and does the device in the videos etc. conceivably do that?" is easier to think about.

I don't think the light has to be confined, and a system consisting of a glass prism with light shining through it should have more mass than just the prism. As a thought experiment, consider a massive particle at rest, and a photon moving with +x velocity. The photon has no mass, but considering the two particles as one system, this is not its rest frame. In the system's rest frame, the massive particle has some -x momentum balancing the photon's momentum. As a system, the particles' kinetic energy contributes to the system's rest mass. Likewise the prism+light's rest frame would be different from the prism's rest frame. I don't know if this is meaningful in general, since spacetime curvature depends on how the mass is distributed, and I can't imagine how to describe the effects of unconfined photons. However there are cases where it is meaningful, such as with a "kugelblitz", a black hole created by a dense concentration of light energy for example.

Yes, but gravitational potential is a Newtonian thing, and that applies (always) in a Newtonian analysis. I was going to use gravity assist / planet flyby as an example of how an object can climb out of a gravity well using less energy, in a changing gravitational field. However, in Newtonian physics, the planet's gravitational force acting on the object equals the force of the object acting on the planet, and the object still uses the same energy to climb, it just gets it from the planet. So it's not the case that a dynamic system alone breaks gravitational potential's path independence. GR is a different system, and I don't understand where and how the analogy to gravitational potential fails. But for example, I read that if you separate two masses, the GR analog to gravitational potential depends on if the masses are spinning, but the Newtonian gravitational potential doesn't.

A light-like path has a geometric length of zero, so all events on a given light cone should have a geometric (hyper)volume of zero. The interior of the cone would have positive volume (by choice of convention) or a time-like volume. The elsewhere would have negative or spacelike volume. The union of multiple light cones should have zero volume.* So for example if you have a light on the train, and turn it on at the beginning of the train's "life" and off at the end, then the geometric volume of all parts of the train that are lit over its entire life, is 0. If you consider only the lit part of the train (chop off everything outside the "light on" event's future light cone, and everything inside the "light off" event's future light cone), the train's entire existence has 0 geometric volume. Am I thinking about that reasonably? If so, I'm not sure if an invariant volume would make sense. It seems like a long-lived train, treated as a bunch of time-like world lines, should have a time-like volume. Or could you add up all the time-like world lines and get a different volume? * Or... did I make a mistake here? Maybe you can't just add up two light cones, because there are space-like intervals between events on the different cones, but then there are also time-like ones... Now I really don't see what a geometric volume could possibly mean.

I mean between two events. I'm reasoning that if two clocks are identical except for their histories (basically, same place, time, and speed), they must tick at the same rate, and have the same time dilation factor relative to some distant clock. Therefore the time dilation factor between two clocks can't depend on "how the clocks got there" (I'm generalizing), yet a calculation of something representing gravitational potential, could. I've never heard of the virial theorem. It looks not basic enough for me. I should look at the derivation but I'd probably give up after getting lost at the top of page 1.

But there is a unique single value gravitational time dilation factor between two points (in your example at least). Elsewhere on the web I see that gravitational potential represents the metric only as an analogy. Then the resolution might be that "gravitational time dilation is determined by the metric," while it's not always applicable that "gravitational time dilation is determined by gravitational potential"?

Resurrecting this idea, that I never ended up wrapping my head around... Say we use a mountain as an analogy for an arbitrary spacetime. There's a clock at the top. Two travellers each transport a clock down the mountain along different routes, and meet at the bottom. There, they generally find their clocks have aged differently, but the two clocks, together at relative rest, are now ticking at the same rate. Their clocks tick at a different rate from the clock at the top, but of course the two clocks at the bottom share the same time dilation factor relative to the one at the top. Therefore there must be a scalar number that relates the two locations, that is independent of any differences in how spacetime is curved along the different paths between the two. In this analogy, "height" works as that single scalar, and gravitational potential is meaningful. Is there another such scalar that relates two locations in an arbitrary spacetime, or is it just the "time dilation factor", and that factor isn't completely determined by any other scalar factor alone? Or, is it that gravitational potential loses meaning only where there aren't worldlines between the two locations? Or to ask in a different way, if you have two particles in freefall with different velocities, that pass through some one event and later pass at some second event, is gravitational potential certainly meaningful along their respective freefall paths, and if so is it the same along both paths, no matter how asymmetric the spacetime is?

2*sqrt(2) cm is the length of the square inscribed in the circles, which should make it easier to figure out.

I agree. Interesting that you reasoned it out right from the start, and transferred the events from the train to the tracks, at rest in their frame. Was that essential to the reasoning, or just because that's what the question asked? (If I could redo the question, I'd make them ships in space without the tracks, but would that make the question harder to reason?) Reciprocality should become pretty intuitive given the first postulate, it seems like a major prerequisite to understanding relativistic effects.

Yes, they're 100 m apart in the train's frame. The strikes / tunnel can't be 1 m in the track frame unless that 1 m expands to 100 m in the train's frame, which it doesn't. Yes, I used 'abstract' incorrectly. It's the added object (like a ruler, train platform, extra tunnel etc.), used to conceptualize the distance, that's abstract.

Err, too boring? Or not intuitive enough? How about, "What proper length of tracks is contracted to 100 m in the train's frame, if the train with a proper length of 100 m is contracted to 1 m in the track's frame?"

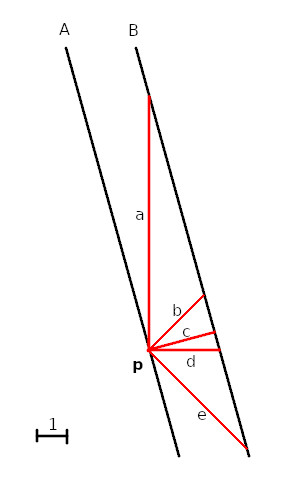
What is the length of a line segment that connects line A at point p, to line B? Is it one or more of a,b,c,d,e, or something else? If line A represented the world line of the front of a train, and B the world line of the back of the train, what is the length of the train? This doesn't even illustrate length contraction or the rules of relativity. I think you're missing some basic geometry in what you're asking.

"One timeline" is meaningless to me. t' inside t is also meaningless... you're effectively asking if the time measured by one clock is inside the time measured by another clock. But you could say that if Bob leaves the train at 2050 and returns to it at 2100, its world line between those events is within the future light cone of the train in 2050, and the past light cone in 2100, and that's what you want: all observers agree that Bob's trip happened after the 2050 event and before the 2100 event. However, if Bob didn't start/end near the train and was always far enough away, that's not true for all observers. As well, Bob's cousin Babs, who suppose shares Bob's inertial frame and clock for an inertial part of Bob's trip, but was in the Andromeda galaxy during proper time interval t', is completely outside the light cones mentioned, so in that sense t' is not "inside" t, and far away events occurring at proper time t' can be before, during, or after (depending on frame of reference) the t interval from 2050 to 2100. Yes, the block universe has one time dimension, but you can choose it in different ways (as MigL said, "You can have many different 'foliations' of the 4D hypercube, and all are equally valid.") If you have the block universe in coordinates so that the front of the train is always at the same location with one x value, its world line is a straight line aligned with the T axis. But you can rotate (hyperbolicly) the block universe so that Bob's world line is now aligned with the new T' axis, and the train front's world line span different x' values. This doesn't imply multiple universes, blocks, trains etc. any more than someone in Russia having a different vector pointing "up" than someone in Argentina, implies that there are multiple Earths. Say they each have a y-axis that points "up", you have one Earth described using 2 different sets of coordinates, each more appropriate than the other to some observer.

I was thinking about this as an example for another thread but thought it would only add confusion. Say you have a train with proper length 100 m, traveling so fast that it contracts to 1 m according to the tracks' reference frame. Suppose that in the train's frame, lightning strikes the front and back of the train simultaneously. How far apart are the lightning strikes on the track? Can anyone answer this with just a few seconds thought? I can't, I have to figure out the details and calculations, but if I ask a different question... They're the same question, but only one seems intuitively obvious.

There are events on the those same 2 world lines that are 100 m apart to that observer, yes. They're on the same world lines, but they're not the same pair of events that are 1 m apart in Bob's frame. The two observers use different time coordinates, and 2 events at the same t and 100 m apart in the train's frame, don't have the same t' value in Bob's frame. The 1 m length of the train that Bob measures is between 2 events on the respective world lines with the same t' value. This is "relativity of simultaneity." Using world lines instead of lengths isn't going to change the details of the simpler examples you're using them to represent. I suppose we persist because we expect a response like "That's something I don't get, let me try to understand that first" instead of "What if I ignore all that and ask the same question in different words?" Block universe, world lines... it's like expecting to find some aspect of relativity for which the rules of relativity don't apply.

I did mean the same thing, but failed to state it. I should have said I meant the spatial distance between two events at the same time in a particular frame of reference. Did I imply the invariant length of a spacetime interval? ...thus proving my point that you have to specify these details for things to make sense to others!

That doesn't work unless you know the time at the light source, and you can't measure that from the detector. You theoretically can't measure the one-way speed of light, but you don't have to measure it since it is by definition equal to c. You can measure the 2-way timing of light, and find the one-way speed because literally by definition, the time that it takes for the light to go 1 way is the same as the time it takes to go the other way. You can however confirm that light from a distance D takes the same time regardless of the motion of the light source. For example, if you have 2 sources moving in opposite directions, and a signal from each of them when they're at the same location, you can verify that the 2 signals arrive at the same time. You don't have to know what time they're sent at, if all you care about is that they were sent at the same time, and you can make sure that happens by sending them from the same location.

Your line of questions shows you're not going to understand the answers. Why don't you start with simpler concepts first and understand them before talking about world lines? The world line of a particle is made up of all the events in the particle's entire lifetime. You're asking for the distance between two arbitrary lines. I think what you're really asking for is the distance between particular pairs of events on those world lines, but you're not specifying that unambiguously. If you're using coordinates where Bob's world line remains fixed at one x,y,z location and only varies in T, then (based on the situation you've implied), the distance between a given event at time T1 on the world line of the front of the train, and an event at the same time T1 on the world line of the back of the train, will be 1 m apart. If you use other coordinates, you'll get other answers. If you're talking about measurements in the block universe, you should specify what coordinates you're using. If you're talking about observations, you should make it clear what frame of reference you're using. If you're measuring the distance between 2 objects over their entire lifetimes (ie. world line) you should make it clear what time you're talking about. And if you're talking about a single moment across a distance, to even make sense of that requires the set of coordinates or frame of reference! If you want specific answers, your questions have to make sense, and they haven't been.

Could you please stop taking what is said and twisting it to fit your existing misunderstanding? It's been repeated ad nauseam that that there's only one train. No, because those are 2 different coordinate systems. For example, the front of the train can be at rest at x2=0 for the coordinate system of an observer at the front of the train, while Bob might use a coordinate system where his ship is at the origin and the location of the front of the train is x1=several light years and changing. If the front of the train enters a tunnel, that's an event. Everyone agrees that the location of the front of the train coincides with the location of the entrance of the tunnel when it enters, but that could be at x2=0 and x1=several light years. Though it might make more sense with all the other basic stuff about relativity that I'm sure you've read, if you called them x and x' to denote that they're different coordinate systems.