md65536

Yes, exactly, so we can discuss what would happen or be seen in a particular model of a black hole, but must be careful not to make the same claim for just "a black hole" in general. Having the universe's entire history in your causal past would describe a particle that is stuck on (or asymptotically approaching) some horizon, with a proper time that approaches infinitely slower than the rest of the clocks in the universe. That would be similar to an observer who could hover infinitely close to a Schwarzschild BH event horizon. So, EM repulsion exceeding gravity would make sense... it would be like the BH itself is causing you to hover (but this is inside the EH, so I don't think infinite energy would be needed?). I think the singularity still exists in those types of BHs, but with different geometry.

Looking for more details, I came across this: Falling into the Schwarzschild black hole. Important details S. Krasnikov https://arxiv.org/abs/0804.3619 which is surprising, but is a reminder that the details describing a Schwarzschild BH can be vastly different for BHs in general. The Kruskal diagrams are of Schwarzschild spacetimes.

This is wrong, as Kino wrote and the diagram shows. It seems you never lose sight of your feet, even if you dropped them in ages before the rest of you went in, but you'd also never see them hit the singularity (of course). You just see older images from when they were above where you are now, and there'd be a last possible image of them which depends on how long ago they entered, so I suppose they'd have to appear increasingly red-shifted.

That's an interesting point. Indeed, "Earth" receiving your message in the far distant future would say "that never happened." If your head could at that point, separate from the feet and escape the black hole, it could go from its local inertial frame where the feet crossed, and return to Earth where the feet never crossed. That seems weird, but it's no weirder than the Andromeda "paradox". Everyone here agrees one way or another that the head while outside the EH never sees light that originated inside, so nothing contradictory is measured by anyone (no observation of an event that can later be said not to have happened). The astronaut saying "my feet have now crossed" is a red herring that suggests there is a paradox when there is none. Without that, the astronaut simply sees images of her feet from outside the EH while outside the EH, and from inside the EH while inside. The details are the same, but may be easier to think about? I think it's obvious if you look at it in terms of intersecting world lines and light cones. I don't know the calculations, but it's easy to see using diagrams of lightcones made by people who've done the calculations. Also, it's easier to think about what information is available to an observer, and not about how it would look. If the object's world line and an event's future light cone intersect, that object "sees" the event. Those are invariant and can tell you what happens without needing to describe it in a given observer's local coordinates. Because the coordinate speed of light at a distance inside the BH is not c, there's going to be visual distortion at some point, and you will lose sight of your feet eventually as the light cones narrow as you approach the singularity (before, after, or during the inevitable spaghettification?, I don't know), but that doesn't always need to be figured out. Interesting! The red lines show light from toe to head going from a lower r to a higher r outside the EH (pink), constant r on the horizon, and from higher r to lower r inside the horizon. A 45 degree line toward +X anywhere in those regions would have those properties.

But the future light cone interior is in the direction of the BH interior, that doesn't matter? Is it that the EH is a null surface, but also a light-like surface, yet the latter does not give you enough information to define the horizon? My main argument in this thread is basically that you can see what is below you, because it doesn't involve a photon increasing its r-coordinate, but rather the observer decreasing its r-coordinate to reach that light. Is that argument wrong? Inside the horizon, the r-coordinate of all photons must decrease over time. Near the horizon, the photons aimed "upward" decrease r very slowly. By necessity, an infalling object must decrease in r faster than some of its photons could---the object can't leave the future light cone of a past event on its own world line, and fall slower into the singularity than all of its light. This implies that an infalling particle can decrease in r faster than the "upward"-directed photons from events on the world line of an object below it. Thus, the infalling observer must be able to see objects that are always below where it is now, but were above where it is now when they emitted the light the observer is now seeing, which appears to come from below. In Schwarszchild coordinates (I think???) those photons are decreasing r very slowly, but in the observer's local coordinates they are moving upward at the speed of light. Just like the EH has a fixed r coordinate but locally moves past the infalling observer at the speed of light. If this is wrong, I don't see how the astronaut could see their own feet, because their feet are at a lower r coordinate.

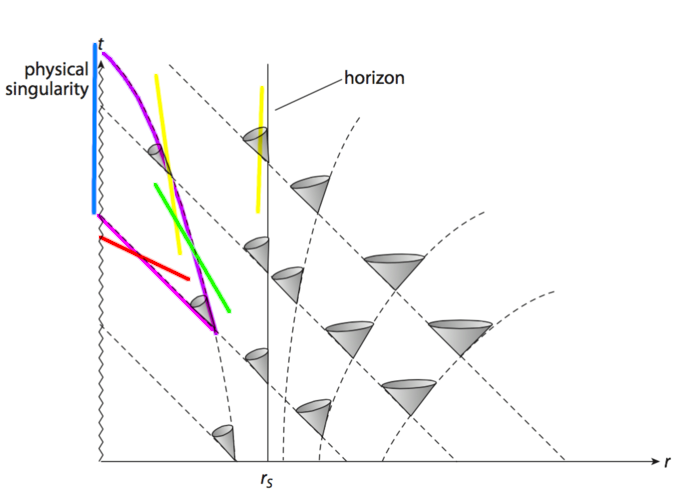
re. "The path of light that goes from feet to head also leads to the singularity." Sure, I'll use another diagram: Here, the purple line could represent a path of light that goes from an event at the feet, and intersects the head's green world line, and ends up at the singularity. The pink line represents light from an event, that is aimed 'directly' toward the singularity. It has a slope of 45 degrees, representing a coordinate speed of c. No object anywhere on this graph can have a slope shallower than 45 degrees. Purple represents light from the same event, directed as close as you can get to away from the singularity. As you can see, it still reaches the singularity. Blue represents all the locations at which light from the one event can reach the singularity, at different times. Red represents an impossible object that "catches up to light" directed away from it. This is impossible, as has been stated a few times in this thread. No path can go from the right side of the pink line, to the left side of it. Yellow represents some impossible objects travelling faster than light in the "opposite" direction. No path can go from the left side of the purple line to the right. Green represents a possible world line for an object, that is traveling slower than light, and sees the event (when it intersects the purple line). Green could be the world line of the head. Even though it entered the BH after the feet, light from the feet can still reach it. Notice that at no point is there light moving away from the singularity. Notice that the possible paths for light from the event are not all the same, or same length. Their different slopes represents different coordinate speeds (in the graphed coordinates) of light. Inside the EH, all velocities in these coordinates are toward the singularity. The vertical alignment of light cones on the EH represents a coordinate speed of light equal to 0 for light directed away from the BH. There is no "catching up to light" needed, because the light from the feet that intersect the head's world line is aimed *toward* the head, as well as toward the singularity. MigL is simply wrong, using arguments that apply to a stationary or distant observer, applied incorrectly to an infalling observer. We can all agree at least that it's possible to survive falling into a large enough black hole without tidal effects ripping you apart, correct? Writeups about this can be found everywhere with a simple google search. Is anyone arguing that those are all wrong? What does it mean if you can survive falling through an EH intact, but you lose sight of your feet? You lose feeling from your feet, and your heart for that matter. You lose blood from your heart. You lose the half of your head underneath your eyeballs for that matter! What does it mean to survive intact, not be ripped apart by tidal forces, and yet be literally cut off from your body because light has suddenly taken on a completely different local behaviour? No, you're purposefully neglecting that light takes time to travel from the feet to the head, about the same (in this scenario) time that it takes the EH to travel from the from the feet to the head. This all implies the astronaut has a meaning for the use of the word "now". If the astronaut can say that the feet cross the EH "before" the head, then there is a meaningful point where it can say the feet are now inside and the head is not. If what the astronaut "sees" is also what the astronaut calls "now", then by necessity the head and feet passed the EH at the same time, and Earth does not receive that message. Either way, there is no paradox, there is no path of light from inside the EH to outside, and there is no point where the feet suddenly disappear because delay of light ceases to be a thing.

I agree, that would be better. Wouldn't the shape and orientation of the light cones be independent of the motion of the light source?, while the shape of the source's world line would be entirely dependent on it. So not all world lines would be pointed locally along the axis of the cone. I think the image is a fair representation of the world lines of inertial particles entering the BH at near the speed of light, which is not at all what I wanted to show.

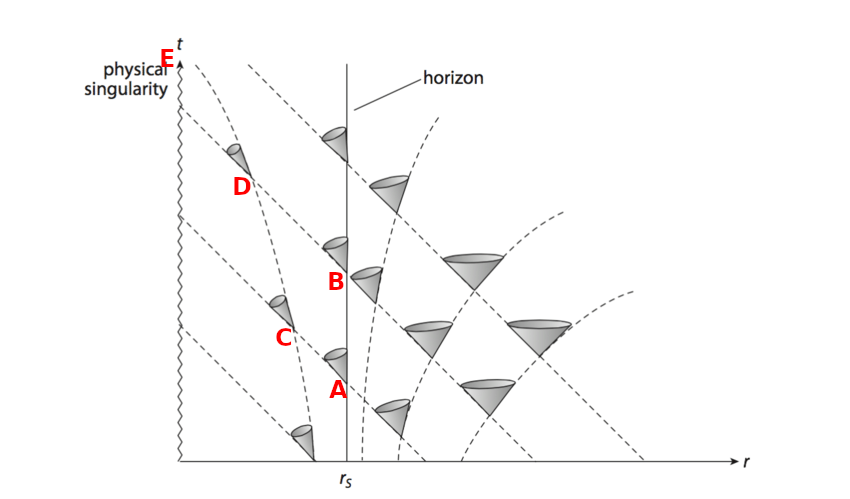
I've attached an image showing light cones inside the horizon. The labelled events are: A - Feet pass the EH. B - Head passes the EH. C - Astronaut twitches her feet D - Astronaut sees her feet twitch E - Photons from twitched feet reach the singularity. The scale of this is out, the astronaut twitches her feet in the short time before the head has entered the BH. More realistically, the head's world line would be very close to the feet's. The light cones inside the BH show that light from a single event does not take the same amount of time to reach the singularity, in all directions. Also... I think I made a mistake, the lines I'm using as the head and feet worldlines appear to be light-like. Can you see from the diagram as-is how it should look, or should I post a correction? Also, if you still think the head can't see the feet inside a BH, please show how this would look with light cones.

The slowing of time is only relative. An external observer measures the infalling clock slowing relative to its own, but the infalling observer measures their own local clock's proper time ticking at a rate of 1s/s. Their own clock does not stop as they fall into a BH. If an infalling astronaut would lose sight of their feet, and smaller distances, this would imply that a light clock would stop functioning, or at least would stop depending on its orientation. Theory doesn't predict that. I really didn't expect there to be debate after a resolution was posted. You still have light cones inside the EH, outside of the singularity. The cones do not become lines, where there is only one path for light from an event to the singularity. The path of light that goes from feet to head also leads to the singularity. "Light beams aimed directly outward from just outside the horizon don't escape to large distances until late values of t." -- https://math.ucr.edu/home/baez/physics/Relativity/BlackHoles/fall_in.html but they do escape.

Isn't that the same thing? Yes, but if both ships fell in, they could remain close enough to relative rest to not notice, for some time. Just like a person falling into a large enough black hole doesn't feel themselves being pulled apart for some time, even if tidal forces are always present (though negligible here). I'm talking about a black hole so immense that the gravitational effects are very weak at r_s, like an r_s of tens of billions of lightyears. If that's too small, maybe a billion times that! If you make it big enough, you should be able to continue falling toward the singularity for a lifetime without ever noticing you're trapped in a black hole. All the rules still apply, you can't communicate with anyone outside the EH, but the EH has expanded beyond you at the speed of light, and anyone you try to communicate with who hasn't escaped, is inside with you. I can't say what would be observed on the inside of a BH, but my understanding is that accepted theory does not predict any strange local effects of crossing the event horizon, like suddenly being unable to communicate with or see "nearby" infalling particles. By "paradox" I meant it's not a real paradox, just a conceptual problem to resolve.

Regardless of what happens inside the BH, the original scenario doesn't involve any light from inside the EH whatsoever. It doesn't say anything about what happens after some moment when the astronaut's head is less than a body's length from the EH, still outside, still only receiving light from outside the EH. But, I think you're also wrong about what happens inside the Schwarzschild BH. Light inside can still move in different directions. Draw some light cones on a diagram. Yes, all light cones inside the BH will be tilted so that all light paths head toward the singularity, but the light cone from an event inside the EH can still intersect the worldline of an infalling particle. The lightcones do not instantly tilt an extra 45 degrees or narrow and degenerate into a single line, the instant you cross the EH. Basically. Any observer outside the EH will see the object approach the EH but never appear to cross it. The exact measurements will be different for different observers. My example was basically two observers who both fall in to the BH. But sure, you could make the head and feet two ships arbitrarily far apart, and just make the BH big enough. Actually this thought experiment started from trying to figure out what would happen if two ships at relative rest were flying far from a BH so large that they couldn't detect it, such as J.C.MacSwell suggested, but if one ship ended up inside the EH and one was outside. I think either both ships enter the BH and don't notice, or the ships necessarily separate (head rips off), as the outside ship has to escape the inside ship if it is to escape the EH. It causes problems thinking of the BH as a giant sphere whose event horizon can hover harmlessly between the two ships, or between head and feet. It is a lightlike surface. If the head and feet see each other, or the ships are in communication, the EH between them is moving as fast as they can communicate.

I agree with Halc. When the feet cross the EH, the photons making up the image of that, and directed outward, forever remain at the EH, which is a lightlike surface. It's stationary in the very distant observer's coordinates, but locally moves at the speed of light. The astronaut notices nothing unusual because the EH and image move past its head at the speed of light, just like photons from the feet do in usual circumstances.

An astronaut falls into an extremely large Schwarzschild black hole, so large that they don't notice any spaghettification-like effects. Their head can see their feet the entire time, and their helmet is constantly sending information to Earth, say. At some point, the astronaut sends a message basically saying "My feet are now inside the event horizon", and Earth eventually receives that message. Is there a mistake with this scenario? What prevents the astronaut's head outside the event horizon from seeing their feet inside the horizon, and how does that look to them if they're watching their feet the entire time? I have an answer in mind but I'm curious if there's any room for experts to disagree on a resolution, and also curious if fellow amateurs can resolve it with about a pop-sci level understanding. I'm interested in how different the answers might be, so please share if you have an opinion!

Yes, I think you're proving your point. If you don't understand something, it can seem god-like. If you read what Einstein wrote and understand even just parts of it, it's easy to see that it's basically a set of assumptions that match observations of reality, and some mathematical consequences of those, whose predictions also match observation. There's nothing god-like about it. But if you don't read it, it's an unknown, and it's already been discussed that people tend to attribute what's unknown to gods. So it sounds like you're assuming that Einstein's work will become an unknown, but that the stories of Him or His work will survive and be passed on (with language, I guess?). But the same can be said about anything that's known. Science can explain lightning, but if everyone ignored and forgot that, then Zeus could regain popularity.

Why do you think it would turn into a BEC if hot? A BEC involves the atoms being in the lowest quantum states, not highly energetic ones. The laser cooling described in the thread is done to take energy away from the atoms. A layman explanation of a BEC (and possibly completely wrong, others please correct me) is that when a particle's speed is very close to zero (ie. very low temperature), you know the momentum of it to high certainty, so due to the uncertainty principle, you can only know the position of it to lower certainty. With a cloud of particles acting as if the particles are each spread out, they overlap each other (their wave functions overlap) and are indistinguishable, and the cloud behaves in ways that are like it's one macroscopic fuzzy particle (for lack of words), instead of behaving like it's made of many microscopic particles. If the atoms are hot (in aggregate), I don't think there's a practical way to force the positional uncertainly that you need for these effects.

I'm not seeing your point at all. Maybe you can explain, why would a religious person not believe in atheism? Is that similar to what you're asking? Can you describe the analogous point to the one you're making from that perspective, or if it's not analogous, what's the difference?

Most? Do you have data on that? Why would we not believe what neanderthals believed? We could try to understand what they did in the context of the world they lived in, but does that mean we should share their beliefs? I lot of the beliefs of a religion have a god as their core. If ancient people ate raw pigs and got sick, but they didn't know why, they may explain it as "God does not want us to eat raw pork!" Now we understand why you would get sick, and don't need the concept of a god to explain it. It's not like atheists say "I don't believe in god, so I won't believe there's anything wrong with eating raw pork!" Atheists and religious people and neanderthals share a lot of the same beliefs. However, if you believe in something, and can't separate the concept of god from it, but are an atheist, I think that means there's a contradiction in your beliefs. As it is, there is nothing in reality that is inconsistent with the belief that no supernatural god exists.

A laser is practical for other reasons, like being single wavelength, high intensity, easy to direct, and needing a small window into the vacuum chamber. If you had some other setup and a single-wavelength light source that directed photons into the atom cloud, but the photons came from different directions, that would work too. I think all that's needed is enough photons with a) right wavelength b) aimed at the atoms c) symmetric or balanced distribution of directions. If you're talking about fredreload's ideas, I don't agree that any of them improve on what's already been done. If you had a way to scatter light into the cloud to get a distribution of directions, that's great, but using mirrors and multiple laser beams seems much easier. Scattering after the impact is basically how the atoms are cooled. As per the quote provided earlier by fredreload, from https://www.sciencedirect.com/topics/chemical-engineering/laser-cooling So to recap, "in the direction of absorption" is why you need photons coming from multiple directions, and you need a wavelength slightly longer than the atom's resonant frequency so that the photons are only absorbed by atoms moving toward the light source (blue-shifted to the resonant frequency). Contrary to what fredreload seems to suggest (I may be misinterpreting), you need the atoms to release that energy to get them to a lower quantum state. If they only absorb, I suppose you could still cool them, but they won't form a BEC by being in their lowest quantum state.

Which two are irrelevant? Do you mean when you wrote, "Do you not realise the basic mechanics that momentum directed along 2 of those 6 directions cannot affect spin?" I'm not talking about affecting spin, I'm talking about slowing of atoms that are moving toward the laser, ie. laser cooling. If you have 4 lasers aimed at +x, -x, +y, and -y, then atoms with movement in the z direction will not be cooled effectively. I think you don't need lasers aimed in opposite directions, but merely a symmetric distribution of photon directions, to avoid propelling the cloud. 4 lasers arranged like a triangular pyramid might work, but probably not as well. Maybe it's better to use more than 6 lasers, surely with diminishing return. 6 is not "magic", but probably the simplest arrangement needed to get good results. Sorry, I (and fredreload it seems) thought you meant the photons had to have parallel directions, not just that they're lined up with the target.

Scattering seems fine to me. You want photons coming from different directions, because the atoms are moving in all different directions. As long as the wavelength is right, it can slow an atom moving in the opposite direction of the photon. Is that wrong? Why do you want it collimated? Scattering would be less efficient if the photons aren't going through enough of the cloud. You'd use lasers for the single wavelength, focus, and high output. The light being collimated is actually a problem---you need the light coming from different directions---which is solved by using 6 lasers.

The spontaneous emission implies there's a lower limit to the average velocity of an atom that you can achieve, so a limit to the cooling. Even if absorption brought an atom to complete rest, re-emission would propel it in a random direction. Why might a laser be preferred over a flashlight? What are some problems you might run into using a flashlight? By the way, how many atoms are you cooling? How dense is this cloud? You could also try a microwave oven, to bombard it with microwaves. You could add a toaster, and let it absorb infrared. But will that cause spontaneous emission like in what you quoted? And how do you get the atoms moving toward these heat sources to preferentially absorb the light? Why does resonance matter, in what gets absorbed and what is emitted, if the atoms can simply absorb light of many different wavelengths?

It's a different state of matter, but the meaning (according to wikipedia) comes from, "Einstein proposed that cooling bosonic atoms to a very low temperature would cause them to fall (or "condense") into the lowest accessible quantum state". But even if it's analogous to condensing from gas to liquid to solid, those are typically going from higher energy states to lower energy states. Eg. water releases energy when it freezes, it doesn't absorb it. Anyway, a BEC involves atoms being in their lowest quantum state; they must get rid of that energy to form a BEC.

As a toy model just to describe where the energy's going, is the following a reasonable description? Say you start with one million photons moving to the right, and one atom moving to the left. After absorption and re-emitting, you end up with one million photons, scattered in a spherically uniform distribution of directions. The re-emitted photons would have variance in Doppler shift (because they're not necessarily immediately re-emitted?), but the photons re-emitted to the left would be blue-shifted on average, and the photons directly to the right would have no shift on average (basically, if a photon enters the atom from the left, and is re-emitted to the right, that photon hasn't changed the atom's final speed). Also you end up with an atom with near zero velocity. The total energy of the system is the same. I would guess that nearly all of the kinetic energy of the atom at the start, goes into the scattered direction of the photons in the end, and a tiny portion of it goes into the Doppler shift of those photons?

I assume it doesn't. If it did how would it do that? Atoms in a higher energy state? Even if it were possible, it couldn't be done forever. That would mean the more time spent cooling the cloud, the more energetic it would get.

Sure, but what is meant by "use"? The energy is not reduced through use. Naively I can think of it like, photons are absorbed by atoms moving toward the laser, and the kinetic energy of the two partially cancel each other out. But really I think it's more like, an atom absorbs a photon with energy E in the atom's rest frame, changes speed in the process, then emits the same energy E (as one photon? or several over time?) in its new rest frame. In the lab frame, the energy absorbed is less (on average???) than the energy emitted due to the atom's change in speed. --- However, if the light is re-emitted in a random direction, I'm not sure this idea makes any sense. The issue is, the real cooling corresponds with energy coming out of the cloud, not energy going in.