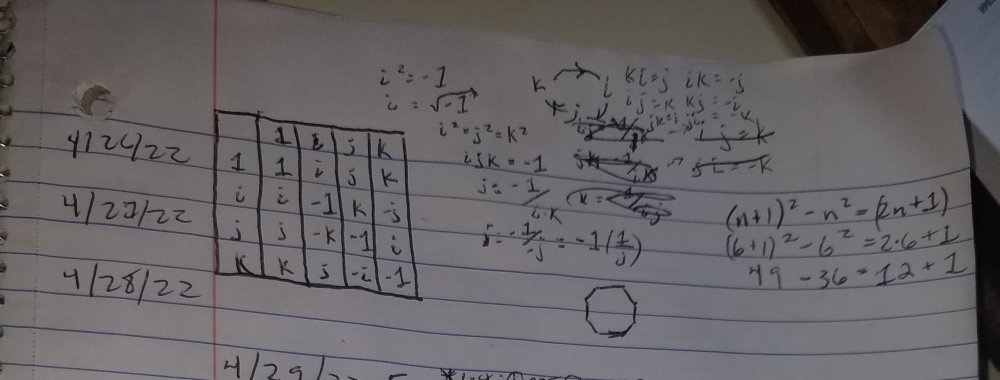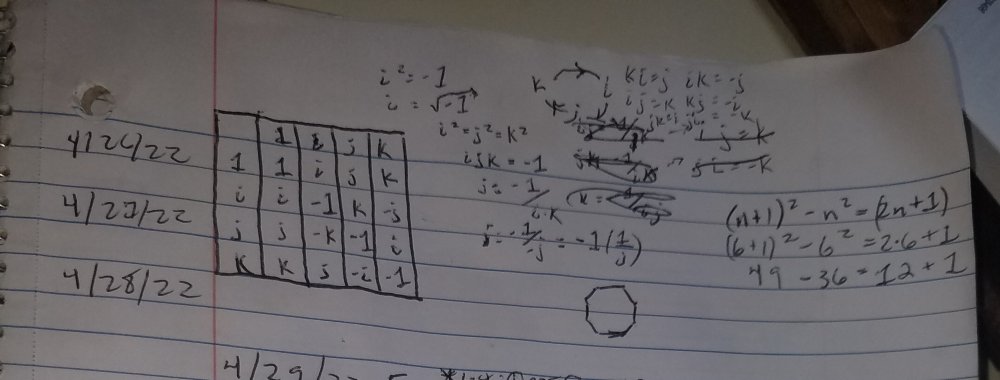-
Posts
286 -
Joined
-
Last visited
-
Days Won
1
Content Type
Profiles
Forums
Events
Everything posted by NTuft
-
defined as the set of square roots of prime numbers, +&-. Inoperable set. -1 and +1 not prime... derivation produces produces Derivation can continue. The level of complexity is characterized as AdS 4 space. The 3-D can be mapped with Quaternion/Octonion algebra. 2-D map on hyperbolic Poincaré disk, or using polar graph, as extension from 1-D "string" (or + - point charge seperation) causes initial planar geometry. The nature of can facilitate quantization at quantum level in the distribution around 0 and as distance increases up to the... Macroscopic.
-

Computations of a cell or solution potentials
NTuft replied to Dhamnekar Win,odd's topic in Homework Help
-
Why is alcohol legal? Since it is entrenched socially and is an established production industry it's a big money maker. It's a painkiller, a euphoriant. It encourages philosophizing. In my opinion ethanol makes you deranged metabolically and probably hurts the brain -- if there's other weakness in the metabolic constitution -- function at low levels, before the damage we see accrue in the liver from having to process it to metabolites assuming inordinate levels over time. Your post is a little strange on the "color commentary" about beatings and what not... but I suppose you round it out as alcohol should be illegal like these other drugs, because look at all the havoc they wreak. I would agree with some points on societies restricting use, but also that enforced restriction seems to create a response of rebellion: don't tell me what I can or cannot do. Counter-revolt by the Libertarian streak against the Nanny state. Whose latest grift?
-
I found the direct application of their same method to be a humorous idea. Having gone around a bit more, I've been prompted to actually read the guidelines and etiquette rules, not sure I read them thoroughly at first. It'd be a bit of work, but maybe a way to set the tone would be to make it mandatory to go through a test. You break the Guidelines and Etiquette into sections that require answer be entered to try to make sure that they were actually read through. Then there could be a cue, like, "Did you fail the kitsch test?" "Do you need to retake the kitsch test?"(We don't want to offend the ladies), as a call to order in a thread that's gotten testy, contentious. Having read a bit about priming, and the terrible problems in the social sciences with repeatable experimental results and data collection methods (see Dunning-Kruger effect), it may be so highly individualized as to how people respond that it wouldn't be worth the effort to set up the test. Save for if members took it upon themselves to try to be externally considerate and insist on the rules when they're infringed on, community policing really. I was probably violating rules unwittingly... And last I doubt the board here is set up for a click-through fill-in-the-blank type test.
-
“You must first of all remember that there are two kinds of art, one quite different than the other — objective art and subjective art. All that you know, all that you call art, is subjective art, that is, something that I do not call art at all because it is only objective art that I call art…. We have different standards. I measure the merit of art by its consciousness and you measure it by its unconsciousness.”
-
Hello @Genardy , What a difficult to inpetret statement! What do you mean by the first sentence??? there is a problem with quantization is it not? @GenadyI took you quoting this (and all you said) to mean you enjoyed [ed: read*] the paper?? What did you think of it? Do you know about electrostatics? Please, your response is very cryptic, I congratulate you. Can I thank you for reading that paper?
-
OK so to continue with the Mathematics, though Euler also had much to do with applied maths. Princeton University has been home to some of the greatest geniuses in History. They also have a small publishing house which publishes specialist topic books, most of which become standards in their field (see another use of the word field ?). I am recommending one about Euler and his constant, gamma to you as you should find much of interest in it. Most of the book is lightly mathematical to be more generally accessible but read the introduction here and see what you think. Gamma - Exploring Euler's Constant Julian Havil - Princeton University Press 2003 & 2021 [...] It bears repeating. To highlight a math aspect: do you see any new applications vis vis ζ(1) or ζ ?(x) It bears repeating. I am missing (10.5 and likely more) but it was worth it finding F-E equation& totient theorem/function, for myself for study. The mechanics bearing transformatinos giving ratios for velocities a/B, T (K.E.) a^2/B^2, U (P.E.) * a^k , I think I understand. Although k is fuzzyto me as degree of homogeneity (e.g. ideal gas law assumptions? uniform distribution in closed space?). We get to where we are transforming (conserving?) velocities, energy, and angular momentum, but here again what looks like t'/t = (l'/l)^1-(1/2)k, then v'/v=(l'/l)^(1/2)k, E'/E=(l'/l)^k, M'/M=(l'/l)^(1+(1/2)k) with l'/l = the transformed path over the original in linear dimensions k in the exponent again looks fuzzy. Of course, we want to conserve these classical physics mechanics... they fit the virial theorem, and at the end of Ch. 10 as cited we have how they behave in a finite region of space if the total energy is 'negative' (see Ch. 15). Or, before that: 2T = kU since T+U = E, by (10.6) U = 2 E / (k+2); T = -kE(k+2) , using averages for T&U and equating avg. E and E proper. I'll not pretend to actually understand the 1 modulo n from Euler's "totatives" business (wow...) but I made a long sidebar in the midst of my notes. Our virial for chemistry appears to me to be broken... Gentlemen, I do not think I am entangled in maths and physics. We need a qay to quantize thosesmall oscillations in atoms/molecules, and the giant forces in particle physics (I think, but I don't know about that). My workup here, however, properly edited, I think is only looking at some math, and quantum chemistry. I do not think there is any appeal to physics exactly -- although the tie-in wit the Hamiltonian isthere... Much like with how much i (imaginary unit) is tied in all over the quantum math. How can we quantize both small and large??? I don't know how to do it, but I think i'm formulating the problem or question at hand properly. Corrections or other ideas of course are welcome and thank you again for prompting more work with yours.a
-
2x e-mails: Re: H2+ and the breakdown of the virial theorem <V>/<T> = -2 Hello, So the average kinetic and potential energy, <T> and <K>, resp., give us <T> + <V> = <E> , and for the 1s hydrogen atom we have <V>/<T>=-2 properly. (pg. 3321) Then, even at our simplest nucleation, H2+, we have a discrepancy: [...] paraphrasing pg.5181, the virial theorem starts to move away from -2 with the H2+ molecule, and already needs "optimization" to fit [...] even though, "...[the virial theorem] is generally true for any system in which the potential energy is coulombic. Equation 7.25 is an example of the virial theorem and is valid for all atoms and molecules." (pg. 3321)[bold added for emphasis] [...] to the issue: could it be that we are miscalculating the Potential Energy because we have reduced what should be a set of values to a constant? It works assuming the 1s electron energy, but something has been lost somewhere where we can't scale up, in "normalization", or in an assumption implicit in Ψ*Ψ to Ψ^2 ; not accounting for what could be hidden in the imaginary unit? What do you think about why the math breaks down at the simplest nucleation, or getting into a 2 electron system, even? I don't know. -------------------------- Re: Addendum on last, cite source. Plus: are we cheating the harmonic oscillator's power series somehow with the "operator method"? We have : "The Schrödinger equation for a harmonic operator [oscillator? it says operator] is -(hbar^2/2mu)*d''psi/dx'' + (1/2)kx^2psi = E*psi As we mentioned in Section 5.5, this is a linear differential equation in psi(x), but it does not have constant coefficients. A standard method to solve such equations is to assume that psi(x) can be expressed as a power series in x: psi(x) =∞∑n=0a(sub(n))xn We substitute this expression into the differential equation and obtain a set of algebraic equations for the a(sub(n)). This method is called the power series method, and is at best tedious. There is an alternative method of solving equation 1 that is based on operator methods, which is not only much easier than the power series method, but is also much more elegant. In this appendix, we shall use operator methods to determine the eigenvalues and eigenfunctions of a harmonic oscillator. Operator methods are used frequently in quantum mechanics and they are well worth assimilating." /\ = "hat" "The Hamiltonian operator of a harmonic oscillator is given by /\H = - (hbar^2)/2mu * d''/dx'' + (1/2)kx^2 =/\P^2/2mu + (k/2/\X^2) where k=mu*omega^2 is the force constant and /\P and /\X are the momentum and position operators, respectively. If we introduce new operators /\p = (mu*hbar*omega)^(1/2)/\P and /\x = (mu*omega/hbar)^(1/2)/\X then the Hamiltonian operator can be written as /\H = [(/\P^2)/2*mu] + (k/2)/\X^2 = [(hbar*omega)/2]*(/\p^2 + /\x^2) Using the fact that [/\P, /\X]= -i * hbar , we have [/\p, /\x]=/\p/\x - /\x/\p = (1/hbar)*(/\P/\X-/\X/\P = (1/hbar)(-i*hbar) = -1 We now define the (not necessarily Hermitian) operators /\a+ and /\a_ by /\a+ = (1/2^(1/2))*(/\x-i/\p) and /\a_ = (1/2^(1/2))*(/\x+i/\p) Using these definitions, we have /\a_/\a+ = (1/2)(/\x+i/\p)(/\x-i/\p) = (1/2)[/\x^2 + i(/\p/\x - /\x/\p) + /\p^2] = (1/2)(/\x^2+/\p^2 +1) [6] Similarly, /\a+/\a_=(1/2)(/\p^2+/\x^2 - 1) [7] Equations [6] and [7] give us /\a+/\a_ - /\a_/\a+ = [/\a+, /\a_] = -1 [?...] Note that the Hamiltonian operator, equation 3, can be written as /\H=(hbar*omega)*(/\a+/\a_+(1/2)) [9] To make equation 9 more transparent, we denote the operator /\a+/\a_ by /\v and write equation 9 as /\H = hbar*omega (/\v + (1/2))" "(pgs. 239-2411) ... This harmonic oscillator WORKS , but if something got left out in simplification or normalization could that explain why when we try to scale up (continuing to use the simplified Hamiltonian operators methods results) we get inaccurate theoretical vs. experimental energy values? @joigus I think there is a "physics" target here, at last. 1McQuarrie, Donald A. (Donald Allan). Quantum Chemisty. 2nd ed., University Science Books, 2008. "Summary: Idea of deriving down to i''' from infinity, potentially establishing number theory from set of sq.rt. of primes, i'. Then, (*highly speculative*) i'' as Kinetic Energy, i'" as Potential Energy from electrostatics for new Hamiltonian in quantum mechanics" QED unless someone can put a hole in it.
-

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
-

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
@uncool, I think the set of counting integers cannot scale against a set with more members as bases, each base of which can be exponentiated to an infinite set itself. But, this is difficult to conceptualize, and I do not know what all axioms we are working under. Apparently ordered pairs are not controversial, but one exemplar to the contrary (or to the contrary of 'X is countable therefore f(X) is countable') can upend an axiom. What do you hint at here? Furthermore, would you recommend any reference on set theory, or other reading/topics on number theories? Also, how do you see a new model of the reals under forcing? In my opinion it is a fine piece of logical proof, but I read into it that it is pointing out how there are infinitely many numbers between any two points on the line because of unlimited decimal extensions. -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
What about using the Gelfond-Schneider theorem to generate a set of relatively uncountable transcendental numbers? Taking all algebraic numbers as the base and exponentiating to a (sub)set of the irrationals. So the intermediate cardinality would be comprised of not all reals, but at least all algebraics relative to the naturals, plus a portion of the reals that makes them uncountable. Thanks for the instruction over the board. P.s. Ordinality. -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
"[...] every square root of a prime number is a distinct quadratic irrational [...] Quadratic irrationals have useful properties, especially in relation to continued fractions, where we have the result that all real quadratic irrationals, and only real quadratic irrationals, have periodic continued fraction forms." "The periodic continued fractions can be placed in one-to-one correspondence with the rational numbers." and hence also with the natural numbers. Is there a bijection of an index that places {i'i'} in with the cardinality of ℚ & ℕ? Or can we find This is again looking to use the Gelfond-Schneider theorem, as I don't see a restriction that the base a can not be a real irrational quadratic, only that it is algebraic and ≠ 0, 1. -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
Non-integers from ℚ for the base? I can understand your point from the example you gave with pi. What I'm trying to do now is find a set composed of transcendentals because they supposedly vastly outcount the naturals, but it hasn't been well defined. So if there were such a thing don't you suppose it would have countability differing from the naturals? -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
I mean the set of numbers from each member of ℕ being exponentiated by the set of square roots of primes. Do you see anything about using the set of square roots of primes as the b component here: ,cited above? -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
{ℕi'}, where 1∉ℕ... ? -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
@uncool My apologies, that may not be satisfactory. If we have the set of numbers, making use of: where a is a prime number, and b is a square root of a prime number. Since this set would be transcendentals, it could be of cardinality greater than the natural set, but would it be of intermediate cardinality under the reals? Thank you 1 https://handwiki.org/wiki/Gelfond–Schneider_theorem -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
I am taking a subset from the irrational numbers | i' ⊆ {ℝ\ℚ}. The set of prime numbers is a subset of the natural numbers. The set of the square roots of prime numbers is not. No, I did mention that, at one point. No, it is obvious, and yes, it is not. I state that there is a subset of ℝ, from {ℝ \ ℚ}, that is of cardinality between that of ℕ and ℝ, "...determine whether there were any infinite sets of real numbers that were of intermediate size, that is, whether there was an infinite set of real numbers that could not be put into one-to-one correspondence with the natural numbers and could not be put into one-to-one correspondence with the real numbers."1 and that is the set of square roots of primes. 1 https://plato.stanford.edu/entries/continuum-hypothesis/ -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
When both sets are increasing "vertically" infintely, but only one has the potential to expand infinitely "horizontally", you think they're equatable? Please, defend your assertion. Also perhaps see the guidelines re: "salad". This conjecture was presented before the current ZF axioms, axiom of choice, axiom of determinancy, MM++ (*), etc. Is it necessary to write it out in set theorem logic symbols? Logic via language ought to be able to suffice for discussion. Perhaps be specific about what it is you can't determine? -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
Rather, going back to the full set of ℝ, we know that the set of square roots of prime numbers (here we'll call them i', a subset of R\Q or P, the irrationals) are enumerated and matched, that these members are then at least doubled by the corresponding negative values of the same non-terminating decimal values, and further outnumbered by all other Reals, then the set ℝ clearly has more members than the set i', thus is of a higher cardinality. Therefore, presuming the forcing procedure described above is valid, 0א = ℕ ; 1א = i' ; 2א ≤ ℝ -

"Disproving" Cantor's hypothesis -- it's trivial, anyway
NTuft replied to NTuft's topic in Speculations
How Many Numbers Exist? Infinity proof moves math closer to an answer https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/ What I am alluding to is akin to a forcing procedure that only opens a further decimal in each member of the irrational subset (for the sake of the conjecture here the set of square roots of primes; I see no reason now why not to use all irrationals) that can then each by itself match the natural numbers as countably infinite. I think it follows that this set is of a higher cardinality than the natural numbers... By what sort of bijection do you suppose to map the naturals, which are infinite but countable, to what is the larger subset of the real, the irrationals, when the irrationals are considered larger than the rationals (of which the naturals are a subset), and the part that makes the real numbers infinitely uncountable? Then in a separate comparison take the set of sq. rt.'s of prime as being fully enumerated as compared to the full set of reals. The set of reals will have other irrationals that can be used in a similar forcing procedure to create the set of sq. rt.'s of primes as subordinate in cardinality to all reals but greater than naturals.