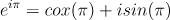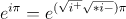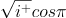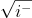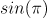-
Posts
286 -
Joined
-
Last visited
-
Days Won
1
Content Type
Profiles
Forums
Events
Everything posted by NTuft
-
Au contraire, mon ami -- the two are inexorably linked I think we would agree, and the Moon model posits tandems of nucleons at discrete points on a definite structure, as I understand it. An analogy would be crystal structure. I do not understand it, and need to read and study more. Hydrogen does seem to be acting funny, but it doesn't have much of a shell now, does it?.. It is like an iota. The table is set with many and various names from the lexicon but some see it as iterations on an iota, or an iota that is paired and by any measure significant. I have not processed what you've actually written and may be responding mechanically. -1 me to 0.
-
J. Diderik van der Waals's "inter-molecular" forces explanation is distance-dependent, and are "comparatively weak, and vanish at longer distances", theoretically. To complicate the matter further, I ask: are we dealing with nuclear droplets, or have we, "flown to the Moon" model, of nuclear structure? I for one do not understand hydrogen bonding, either, and need to review the basics. +1 for exchemist's explanation, and I agree with MigL there is not much to add to address the question properly (caveat: Again, I need to review even these basics). In my opinion the better formulation of Occam's razor states that the explanation needs to be as complicated as needs be dictated by the nature of the question posed...
-
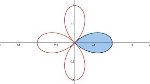
I have always thought of there being parentheses inside the root exponential function. I would argue that the numbers are opposite in magnitude but are the same number, precisely. It may be that I was only trying to find the unit hyperbola, or the complex hyperbolic space. Unit Hyperbola--Handwiki I thought perhaps the vertical (lower, or limit) bounds for the complex graph should be , and the horizontal perhaps when , which would make an ellipse, so the unit hyperbola scaled differently and now with an ellipse... but of course we can not screw up hyperbolic functions: Hyperbolic functions It may be we can already do everything we need to with , but it seems clunky to me... I doubt this is correct or useful either but I had it worked out we could quantize Kinetic Energy with the bound that makes .5 from the function, , or -- set that limit velocity as equal to the mass of the proton. I had Potential Energy for, I imagine, an electron whereby two electrons at (-.25) balance a proton charge (possibly confounding charges and energies...), but, with TI-83 (handheld scientific calculator) I had the P.E. function increasingly negatively (as though the electron were further from the proton), whereas the KE function set an upper .5 bound with and was going towards a limit of 0. I cannot re-create the numbers the same for PE through WolframAlpha computation, and I'm not sure what the exponent should be for PE (3/2, 1.5,...). I will try to only "crank" out what is necessary for this thread. I would not rule out that I thought the "imaginary unit" was kind of clunky, and we could somehow give magnitude to complex numbers if we define the i as being members of set. But, maybe we can do everything with i being the multiplier that signifies a negative root. Lastly I don't know if I can use +1 and -1 as arguments in the function given current definitions, but iterations of +1's and -1/2's for protons and electrons respectively I thought made sense some how.
-
There is a problem with defining the square roots of negative numbers, in my opinion. I went over how I wanted to do that. There are two ways to do it for positive numbers, and I think there are two ways to do it for negative numbers. Also, the explanation on the domain set being mapped onto the codomain by a function, and the many-to-one vs. one-to-many rules are helpful, thank you. I will try to wrap my head around it... Sorry, but I think it will help. Hi uncool. I do not think you have what I am claiming figured. I meant to illustrate in the post I quoted you in above that the numbers you ran on WA were not what I was implying. In the second iteration, still yet, no -- operative is: "with ". Then the imaginary number in the exponent is now that one I've just set, which I then split. I will definitely look into how the McLaurin series is tied in and I appreciate your knowledge about (I imagine) sequences, series(just mentioned), sets (I know), and the postulates, forms, rules and proofs that go into that branch of math, which I bet you know well -- it's not my strong suit. -- "e^(x*i*pi) = x cos(pi) + i x sin(pi) = -x," x=pi already in that equation, no?
-
when = = + = (+1)([cos(pi)=-1]) + (-1)([sin(pi)=0]) = (+1)(-1) + (-1)(0) = -1 I think the positive co-efficient (+1) is there in front of cosine, though i+ is not denoted--since it's the "real" half of the root of -1 ----- using (+1.4142...)(+1.4142...) (-1.4142...)(-1.4142...) (+1.4142...)(-1.4142...) (-1.4142...)(+1.4142...) now with = (i'+)(i'-)=(+1.4142...)(-1.4142...), (i'+)cos()+ (i'-)sin() = cos()+ sin()=()(-1) + ()(0) = - ; since that co-efficient in front of cosine is now
-
+ve number? I think I understand the same. Higher positive number meaning net charge higher due to fewer electrons (-) in the balance.
-
I can't always keep it straight myself, so: Oxidizing agent: https://handwiki.org/wiki/Chemistry:Oxidizing agent https://handwiki.org/wiki/Chemistry:Reducing agent Reducing agent:
-
Al uminum! 🤣 j/k. we'll defer to Humphry Davy 's choice about that.
-
That goes contrary to my understanding of oxidizers and reducers, John. Will they spontaneously react, as Sodium and Chlorine, Nitric acid and Hydrazine, or even Lead and Sulphuric acid ? Or must an initial energy be added, as in your posted video, to get past the potential barrier ? Please explain the reaction process. ( my last Chem course was Gr.13 in 1976-77 ) Are we talking about anhydrous sulfates? What ones? What is a strong enough reductant? Don't say aluminium.
-
We're going off-topic, but, it looks like a job by: https://handwiki.org/wiki/Biology:Dissimilatory metal-reducing microorganisms something weird about their cytochrome c's... CymA and TorC genes or something.
-
Unbelievable overtake. Thanks, I hadn't seen this.
-
"Eaters of rock"... Ever heard/read about the polymetallic nodules on the ocean/sea floor? I don't think they precipitated or accreted over time randomly.
-
x,y,z is given to you as terms that define the ellipsoid. How about you try to define the volume.. centered.. within what is given -- the ellipsoid?
-
set: https://handwiki.org/wiki/Set_(mathematics) derivative: https://handwiki.org/wiki/Derivative differential: https://handwiki.org/wiki/Differential_(mathematics) function: https://handwiki.org/wiki/Function_(mathematics) differential operator: https://handwiki.org/wiki/Differential_operator it'd seem to establish it as a function would only require that the set be mapped to another set. as a function it could then be differentiated, producing the derivatives as proposed. what this entails, i do not know -- it could be a nothing burger. or, it could be a Hamiltonian operator: the potential number of values that can be assigned to objects (particles) as kinetic(i'') or potential(i''') energy are unlimited, and it seems to me a 'gapped hamiltonian' in that the values are discrete with 'jumps' in between. just more speculations.
-
(OIL-RIG) Oxidation Is Loss, Reduction Is Gain [of electrons]
-
Dear @studiot, From page 1: These are my working definitions, and I know they're not correct, so I will look to redefine these terms properly, but, please do impart directly what you think is the most correct or necessary conditions/definitions for the purpose here, if you see fit. I am not able to make LaTeX work properly yet, but I'm reading through that information. A correction may help you recognize the operation : derivation produces produces: I apologize, i do take this seriously. And no, I cannot define all my terms properly, I'll work on it. Your participation is appreciated but is up to you. Thanks
-

Computations of a cell or solution potentials
NTuft replied to Dhamnekar Win,odd's topic in Homework Help
If I write the balanced equation as 2VO2+ + Zn0 + 2H+ ⇌ 2VO2+ + Zn2+O-2 + H2O Is this correct? I do not know. Perhaps split apart the reduction from the oxidation reaction. What is oxidized, what is reduced? Is the start => change of the solution set-up to allow this reaction? Remember they want the E°. -
The grass is soaked in glyphosate. We do not have a representative government, I don't think anyone in the West does. Money's influence on political campaigns here runs the show. As regards the detail from your original post, I don't think the specifics you give are germane to the question. This post quoted here meanders a ways, too.
-

Computations of a cell or solution potentials
NTuft replied to Dhamnekar Win,odd's topic in Homework Help
A standard technique in editorialization is to insert [Ed: ] How can you operate latex on this site, or where would you recommend I find it, please.