joigus

I hereby propose Godwin's second law. Namely:

Yes, it's flat space-time, almost everywhere. It seems obvious, doesn't it? A simple re-scaling of the variables takes you back to Minkowski. When I said "are you sure?" I meant that all the derivatives cancel. That there is total continuity. That "there is no problem", as you implied. This requires a calculation, and perhaps a little thought too. I'm getting, \[ g''_{zz}\left(z\right)=2H\left(z\right)+2z\delta\left(z\right)+12z²H\left(-z\right)-12z³\delta\left(-z\right) \] This is discontinuous because of the step function, not because of the delta terms, which have damping factors as I mentioned before. I had to do the calculation to actually see the step discontinuity. Has this discontinuity come from a sloppy parametrisation of empty space, or does it correspond to a weird distribution of matter at z=0? That's another question. I mention all this because, eg, a cone is flat space everywhere, except at a point where it has infinite curvature. That's why you must be careful and look at the topology, global properties, and so on. It seemed to me you were just blissfully saying it was flat space because a purely formal re-scaling does it. Does Genady's example answer Marcus' question then?

When you construct the Riemann tensor, second derivatives of the metric coefficients are involved, as you well know. As you didn't address my question (only half of it), I'll repeat: Those are certainly involved in the calculation of the Riemann tensor, aren't they?

No, it's ok. It was just me splitting hairs, as usual.

Are you sure? What is H'(z) and H''(z)? You might be right, and I wrong. You might be wrong, and I right. Or we both right or wrong, and not know. In any case, it's interesting.

Tunneling is about one particle going through a barrier a few angstroms thick --I'm thinking Josephson junctions and the like. Star Trek stuff is about sending 1025 atoms many miles away, and these atoms remembering who you where and what exactly you were thinking on the other side. Quite a feat in comparison. For the dark side of teleportation you might want to consider The Fly. Either the 1986 film, or perhaps the classic, 1958.

Sorry, Genady. That's what I should have said. Should have meant? In the general theory of PDE's, as you probably know, the eqs. can be proven to have unique solutions for any complete set of initial/boundary data iff the highest order derivatives can be solved in terms of the rest by Lipschitz-continuous functions (simply continuous is a stronger condition that of course suffices). g''=F(g',g,T,x) where (schematically) g is the "function to be solved for", F is a function, T is a source, and x is the point. Heaviside's step function is not continuous, but you're right that the "damping factors" z² and z⁴ seem to patch up the zeroth and first derivatives, but not the second. I'm next to sure that the moment you second-differentiate, you'd run into problems though. I wasn't critizising your example. I understood the motivation, and it's very nicely devised.

Ah, yes! But this introduces discontinuity in the metric by hand. So it's not a surprise that PDE's (never mind their being non-linear or having a good deal of geometric meaning) cannot encompass them.

I suppose that's what @MigL meant when he said 'sort of'. Here: Just for the record, I don't see the connection either. Not to mention nobody mentioned space-time curvature here. And nobody should.

Just to clarify, I meant reality according to Einstein: (from the famous EPR paper) Quantum mechanics does not necessarily deny reality (in this sense) for a wide range of system properties (energy, momentum, spin, orbital angular momentum...) Position is not one of them because position is not a conserved quantity. What it does is deny reality for certain property-pairings that are classified as incompatible, at the same time. See how naturally the question of causality pops up when one examines this question of reality?: At the same time. There's the relativistic rub. What if a system has spatial extension and one measures one property here and another (incompatible) property there? In QM there is a tension between reality and causality, you see. This 'tension' is more clearly perhaps expressed by way of Bell's theorem. And, as MigL says, every time you measure, this reality is 'updated'. I prefer this term to 'established'. But I have no objection to 'established'.

The mathematics and the rules to apply them are very precise. How to swallow the metaphysical pill is another matter. I was in the process of answering you when exchemist's answer blinked on my screen. I don't think it's about a subtle way of motion, or measuring "things" from a recent past, or something of the kind. I think it's about this beneath-reality physical variable that we call the probability amplitude. I carries energy and momentum and is coupled to currents. It's as physical as it can be. But it only gives you potentialities, what can happen, not what does happen.

Good one. Here's the catch: (my emphasis on OP's source) Nearly a 100 years in the books. And still people, when in doubt between reality and causality, would rather sacrifice the latter. It is reality that is dead as a sharp concept, even though it is a very good approximate one. This goes to show how adhesive the concept of classical reality is: "It's either this or not this" is harder to give up than smoking.

That's an outstandingly good question IMO. I know inverse problems in physics are notoriously difficult. Eg, the inverse-scattering problem: Given the scattering properties, find the scatterer. What you're proposing, in terms of scattering problems, would be: Given any scattering, can I always find a scatterer that does it? My guess would be no too. That you can always find a T that does it, even though you might have to make it un-physical. But I cannot go beyond the guess at this point.

Yes. Scale can dilute our delusions. It shouldn't should it? Einstein seems to have been of the same opinion. I find it very difficult to disagree with that. The most likely candidate to smooth things out is, of course, quantum mechanics. And Genady is very hard to win over, probably because he lives on an island.

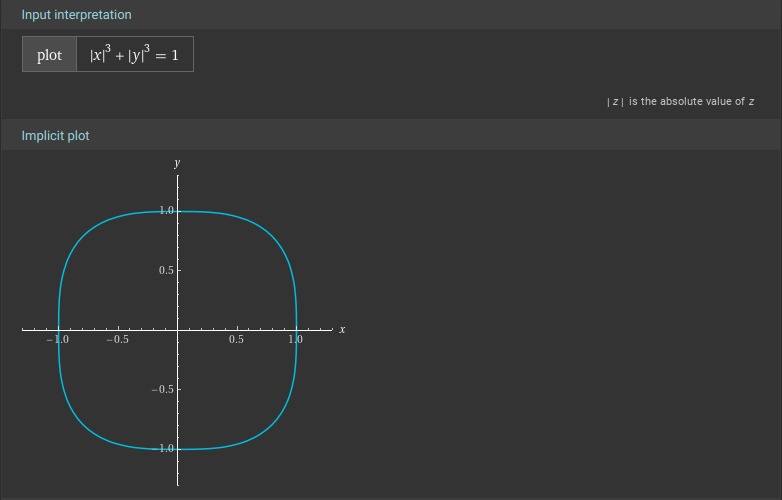
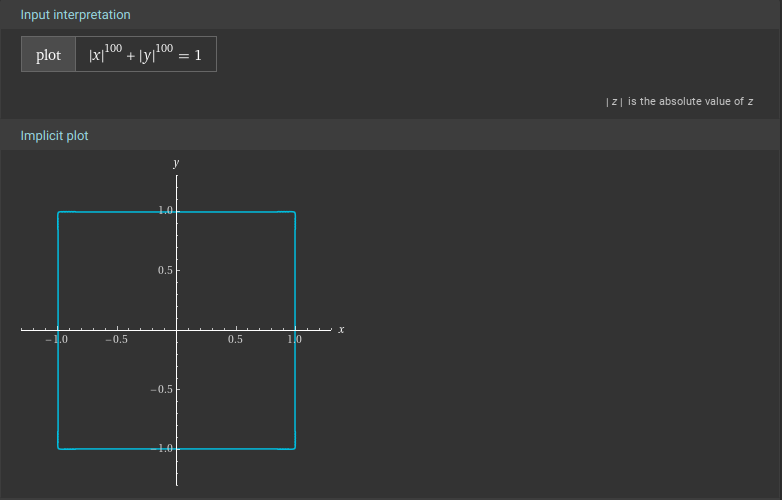
The argument that always creeps in is that, looks (and is) smooth enough, while, doesn't so much, although it's equally smooth. It's just that the curvature at the corners is enormous as compared to scale 1. These are called squircles, btw, and they're fascinating.

I always use pressing Ctrl+hyperlink, as suggested by Swansont. Fast.

Amen OP confused "theory of everything" with "everything I think is a theory".

OK. Then the Wikipedia article needs editing, because it's very confusing. It explains nothing of that. Not a thing.

Sorry I missed this. There seems to be a correspondence between one and the other, right?

Here's what I mean: According to Wikipedia, the definition of LCT's is, \[ X_{(a,b,c,d)}(u)=\begin{cases} \sqrt{\frac{1}{ib}}\cdot e^{i\pi\frac{d}{b}u^{2}}\int_{-\infty}^{\infty}e^{-i2\pi\frac{1}{b}ut}e^{i\pi\frac{a}{b}t^{2}}x(t)\,dt, & \text{when }b\ne0,\\ \sqrt{d}\cdot e^{i\pi cdu^{2}}x(d\cdot u), & \text{when }b=0. \end{cases} \] So it's just an integral transform acting on the time-dependent part of the position-variable representation of the total wave function. IOW, this transformation does not depend on colour, electric charge, weak hypercharge, spin, or any of that. Nothing! It doesn't even touch those indices. How can it provide classification into irreducible representations according to colour, electric charge, weak hypercharge, spin and all of that? I don't see how it does, and I can't picture any way in which anybody can tell me how it does unless they have a theory, as promised in the wikipedia article: What theory? Where is the theory? Does anyone have a theory to explain this utterly unbelievable statement that a group acting on one space helps classify objects defined in another (completely unrelated) space!!!? I know about Cartan, and Gell-Mann matrices, and unitary representations of compact groups. I know all of that. But it doesn't even begin to address any of my concerns about this.

For a whole bunch of good reasons! Mm... Not really. I'm very familiar with \( SU(2)/\mathbb{Z}_{2}\cong SO(3) \) and \( SL(2)/\mathbb{Z}_{2}\cong SO(3,1) \) and their algebras, as with some non-unitary groups. But it is one thing to decompose groups into factors and quotients and do the analysis in terms of Dynkin diagrams, central charges, Casimir quadratics and what have you, and quite a different thing is to state where these groups become relevant and why. And what they help to break apart and study. For example SU(2) can be said to embody how elementary particle "see" rotations in space (example: spin), or... it can also be an internal symmetry group that tells us nothing about space and just refers to abstract directions in the Hilbert space (example: hypercharge). It's still a mystery to me how parametric transformations in the "space" of energy and time (LCT's) is telling us anything at all about transformations in a completely different space (the space of colour, hypercharge, electric charge, and so on). I fail to see how even spin is included in the package. And I'm not any the wiser now. But it's perfectly possible that I'm just too rusty on this, so my apologies in advance if that's the case.

I find it a tad peculiar that the multiplets of the standard model are obtained[???] (correctly AFAICT) from this 3-parameter group that only acts on the frequency-time plane. Really? How does the E,t plane "know" about parity? The multiplets displayed there are sure those of the standard model. And the fact that electrons are called "negatons" doesn't bother me too much. But where do these "boxes" come from? From this group whose only motivation is to generalise and unify Fourier and Laplace transforms, as well as other reparametrizations of the phase? I suppose Wick rotations can be found accommodation there too... I don't know. I've been looking at the more readable page on LCT's, https://en.wikipedia.org/wiki/Linear_canonical_transformation And everything seems nice and dandy until we get to this table with the claim, "a" theory? What theory? This suspiciously sounds like a non-properly-curated addendum to the previous wikipedia article by some people intent on self-promotion. I could be totally off-base, but I find the last paragraph of the wikipedia article very suspicious even though the table is that of the SM. They haven't shown to me to any degree of accuracy or plausibility that the table can be proven from the representations of the LCT. Besides, the LCT is 3-parameter group. The standard model, OTOH, is what SU(3)xSU(2)LxU(1) --> 8+3+1 internal + spin Only counting the compact-group (quantised) degrees of freedom. It doesn't add up in my mind. How did you come across this? What is you interest? Can you tell me more?

I don't think so. AAMOF, ideas like "we live in a simulation" or panspermia sound to me dangerously close to trying to revive the idea of an intelligent creator, but with an aura of scientism about it. All of them (and the ones to come) equally vulnerable to the infinite-regression argument: Who simulated the simulators?, and Who seeded the seeders? etc.

That's from Life of Brian, if I'm not mistaken. I testify to the fact that the teleological argument has been receiving some attention lately. More of a cardiac massage, IMO.

On my part, it's OK. Those aren't bad questions necessarily. Any imprecision is understandable on account of the difficulty of the subject. IMO Mordred's answer was spot on and succinct. I have little to add to what he said. You seem to be bothered by the presence of fields in the geometry though, and that's fair enough. In pure geometry we don't have this arrowy structure we call fields. On top of that they have an algebra of creation and annihilation, and they are complex (have an imaginary part). Those are quantum fields and they seem to go beyond the scope of geometry. Does space-time emanate from the field, or is it the other way? Nobody knows. Maybe there was an eternal inflation scenario, as some models say, and scalar fields gave shape to everything else. It's, as Mordred said, speculation. Highly educated, yes, but speculation after all.