Everything posted by joigus
-
Singular quantum field evolution
I said that. It wasn't Studiot. You headed the quote with "Studiot said". I didn't say anything was sh*t. On the other hand, let's consider this: So before time, there would be no time, but there would be infinite time, and time would emerge, and then it would proceed as usual. This is like landing upside down after a logical somersault. Not much sense to be found here. Again, points have no extension, so you can't have anything be "uniform throughout" a singularity.
-
Singular quantum field evolution
A singularity is a point in time, if you look carefully at a Penrose diagram in GR. How can a singularity be "uniform throughout"?
-
Equilibrium: Why is products assumed to formed in equal amounts ?
When you contemplate the red-ox aspect of chemistry, right. Then you have to account for charge conservation as well in the partial ionic reactions. It's often a clue when you don't know all the atomic/molecular participants in detail. Thank you for pointing it out. Stoichiometric balancing is about number of atoms. red-ox balancing is about electron, proton, and sometimes hydroxide-ion numbers, depending on how acidic the medium is. It's all about protons, neutrons, and electrons. Nothing else. There are no nuclear re-arrangements. I was somehow feeling the student is not busy with balancing electrons yet.
-
Singular quantum field evolution
What does it mean to be "infinite in scale"? I cannot process the "or". It produced in me the intellectual equivalent of a blood clot.
-
Equilibrium: Why is products assumed to formed in equal amounts ?
Just to clarify in case there's any doubt, @swansont 's answer and @KJW 's are pointing to one and the same principle: Atoms are conserved in chemical reactions. Stoichiometry is nothing but a book-keeping tool for that experimental fact.
-
What is a metric space ?
Physicists be like, "dual space? That's nothing but a fancy name for covariant vectors". Mathematicians be like, "No, no, no, physicists! You must take the dual space seriously. It has a life of its own!" Bilinears meet you half-way; wink, wink. Very interesting topic BTW, @studiot .
-
How would you counter the "science was wrong before" argument?
I didn't get this concept from science. Karma is not a scientific concept, so I could hardly have got my meaning from science. I got it from Mahayana Buddhist teachers, for whom karma is a common concept. And they told me it's Sanskrit for "cause and effect", or "deed and consequences", or sometimes consequences from past events. According to them, you can even carry karma from previous lives. According to Mahayana Buddhism, not science that is! It's very clear, eg, from the Wikipedia article: I'm sorry. That wasn't addressed to you.
-
black hole event horizon basic question
Yes, good point. The question about the dimensions of the infalling object are still relevant though, IMO. Imagine a humongous space station with parts wildly separated in comparison to the Schwarzschild radius. Arguably, the tidal forces can be made relevant by making objects extense enough. After all, the equivalence principle is only exact locally. (Sorry I didn't follow up before; I was on a short vacation).
-
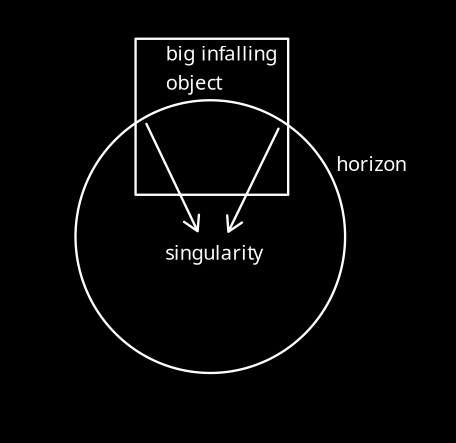
black hole event horizon basic question
Depends on the radius. Honestly, I don't know what the real thing would be like, but if the black hole is small enough in comparison to the body's dimensions, the tidal forces would be enormous. The spaghettification conjecture comes from the difference in the direction of the forces corresponding to different points of the big object in the picture below, which represent the tidal forces. Whether this results in ordinary matter turning into a spaguetti of quarks and gluons, as I've heard said, I don't know. The picture is very exaggerated, of course, in order to illustrate the effect clearly.
-
black hole event horizon basic question
Just an aside: You also must assume a very big BH in comparison to your body size... Anyway. But your heart keeps falling towards the horizon. It's not like it's kept outside it, like I understood you meant when I pictured an enormous radial acceleration. So your blood would keep circulating as far as I know. Yes. If the radius is big enough you wouldn't be able to feel any noticeable effect, if the theory is correct. That's just the equivalence principle at work. Now, if there are forces involved... the problem suddenly becomes more involved, IMO. Forces other than gravitation do not transform in any simple way I know of. My guess is that you would be unable to pull the rope and, quite unaccountably to you, it would have turned "rigid" (again, assuming the BH is really big and tidal forces are not noticeable).
-
black hole event horizon basic question
Free fall. Orbiting is falling. Remember Newton and his famous apple. Ok. I see what you mean. You wouldn't be able to pull back the rope. But that's not the same case as falling through the horizon. Why is that a contradiction?
-
black hole event horizon basic question
If you lower a rope below the event horizon you will experience a humongous gravitational field. You are standing "still" against one of the strongenst gravitational forces in Nature. If you cross the event horizon in free fall, you don't "see" any gravitational field at all. It feels like empty space. It's a matter of frames of reference.
-
Radical question about Particle formation?
😉 Much has been known to confuse Many.
-
Radical question about Particle formation?
Stop talking to much. Much doesn't seem to be helping. 😉😉😉
-
Dynamiting Quantum Mechanics via Theorem of Universal Determinism
I suggest you try your luck on https://physics.stackexchange.com/ or https://math.stackexchange.com/ Or maybe try a professional publication; the likes of Foundations of Physics Letters, for example. FPL is concerned with fundamental questions like the ones you are proposing. The stack exchange platform is more for questions concerning mainstream science, with no room for speculation. In FPL they will give you what will feel like a fair hearing. It would be interesting to know how your idea has fared over there.
-
Dynamiting Quantum Mechanics via Theorem of Universal Determinism
You missed the point. It's quite pointless to try to be specific about something that doesn't even start to make sense. You're not using the words "proof" or "theorem" in their usual sense. No, they don't. I've proved many theorems. I know what is like to prove a theorem, and the different techniques: direct proof, reductio ad absurdum, mathematical induction, etc. Yours is not one. No. Nein. нет. いえ. Your variables are neither local nor non-local as you have proposed no particular model. An interaction involving additional dimension in the simplest form involving functions and finite-order derivatives would be local. You would need specific non-local couplings involving infinite-order derivatives to be able to claim the interactions are non-local. You don't do any of that, so. Your claim is empty. I can ellaborate on that, but I will essentially tell you the same again, and again, ang again... You keep saying this, as if you were making sense. It doesn't magically start to make sense when you say it for the eleventh time.
-
Is Mathematics or Physics the Real Mother of Science
The mother of crackpottery. The ancient Egyptians and Babylonians, Chinese, Indian, etc who started studying the mathematics of the real world, probably wouldn't know the difference. They wouldn't be able to say whether they're doing physics, or mathematics, or geometry, etc.
-
Dynamiting Quantum Mechanics via Theorem of Universal Determinism
There was no proof. You can't find an error in it because it was a chain of fuzzy statements. If I say, "this person is a 27% flamboyant", there's no way to prove that wrong. It's neither true nor false. It's fuzzy. The terms are ill-defined. The "error", if you will, is in misusing the terms, skipping definitions, etc. There is no proof of this either. It's impossible to say anything about determinism or the lack of it if there is no rule of evolution or updating. Additional dimensions don't do anything to the deterministic character if the evolution equatioins are stochastic. I was thinking very much the same thing. Claiming that hidden dimensions make physical systems deterministic would have those play the role of hidden variables.
-
Information paradox
I meant "infinitely many different microscopic states..." The "different" bit is essential. I'm not sure what you mean by this. The conditions of a BH are not applied to the rest of the universe AFAIK. Black holes are very special systems. Although it's true that there are so many. They're not rare objects by any means. The problem with the BH is that while incoming particles carry distinctions, as Susskind likes to call them, and gives back always the same boring thermal state = one "distinction". A "distinction" is a particular choice of initial conditions (position and momentum). In the parlance of classical mechanics, different choices of initial conditions (so-called points in the phase space) always end up being sent to different points in this space of dynamical states (final conditions.) This, in classical mechanics, is called Liouville's theorem, and is understood to imply conservation of information. In quantum mechanics, the generalisation of this law is called unitarity. And the picture of particle-antiparticle pairs is basically right from what I know. Virtual particles are something of a mathematical artifact, but if given the right energy by the appropriate interaction, they "become real", which means the vacuum (virtual loops appearing and disappearing) gets promoted to the first excited state (actual particles that can be seen by a detector). I hope that was helpful. Quantum fields + gravitation are kind of a jerry-built machine, with no proper theory to be sure about anything.
-
Information paradox
The information paradox is not about our ability to trace back the microscopic history of a system. The microscopic history of a big-enough system can never be followed exactly. The initial state of the 1024 or so molecules in a sample of an ideal gas in equilibrium cannot be traced back, and it never will. This is a consquence of molecular chaos. The arguable loss of information from the information paradox is a more serious problem, if it responded to an actual phenomenon. It would imply that infinitely many microscopic states would evolve towards one and the same microscopic state. It would be, not a matter of us not having a clue, but of a clue not being there at all, so to speak.
-
The Nature Of Spacetime Two
That's a good way to put it, I thnk. The interesting point, at the risk of getting silly is, provided there is something (electrons, curry,...), why is it 3D? (Or 3+1, including time). Maybe 10 years in the future someone can think of a consistent way of looking at spacial dimension as an observable that can be assigned probabilities in the proper generalisation of quantum mechanics (with testable consequences). And for some reason, we are bound to live in an eigenstate of that observable with D=3.
-
The Nature Of Spacetime Two
There could be faint hopes of some day testing with gravitational waves and such. This is because GW can probe farther and earlier than any other signal. Maybe. But at this point I think the situation is better illustrated by a professor's famous words "think of this as..." In the same spirit, I tend to see space as a property of both curry and electrons, not so much as a thing of itself.
-
The Nature Of Spacetime Two
Dirac once suggested that the laws are essentially the same, but the category we understand to be "universal constants of physics" evolve with cosmological time. The idea of a multiverse suggests the different values for the constants of physics are a consquence of local phase transitions in wide ranges of the universe. Other people have suggested the existence of some (one would think unfathomable) meta-laws of physics for which the present laws are a transient phase. I know Smolin and collaborators have been working on some kind of analog of Darwinian evolution for the laws of physics. The very fact that there are so many ideas in that direction and apparently nobody has been able to formulate a precise way to propose an experiment to test them, to me speaks of a domain of undecidability or non-falsifiability.
-
Dynamiting Quantum Mechanics via Theorem of Universal Determinism
Oh. OK. I understand. I wouldn't say those neutrons are not identical. I'd say they are in different quantum states. As to hidden variables for the neutron, according to Bell's theorem, you cannot assign hidden parameters that determine any objective internal structure to a neutron, as SU(2) is a subgroup of SU(3), which is an exact symmetry for neutrons. And SU(2) is exactly the group that Bell used to build a set of three observables that cannot have simultaneous elements of reality. Present physics could, of course, be wrong, but the present status of our understanding is that neutrons just decay when they decay. And it seems hard to attribute that to any "internal" mechanism, at least if we don't want to resort to superdeterminism. I do believe elements of reality can be ascribed to position variables through gauge particularisation, which would "protect" them from being known with certainty, but not to spin or any SU(n)-related variables = "internal variables" = "based on a compact group". But that's a different story, it's not mainstream, and just my thinking.
-
Dynamiting Quantum Mechanics via Theorem of Universal Determinism
What is untrue? That neutrons decay time cannot be predicted? Of course there are many different situations for neutrons. Lifetimes of bound neutrons can be very long indeed. Slow neutrons can couple to a nucleus and prolong their life, etc. If and when they decay cannot be predicted though. Neutron decay time cannot be predicted.