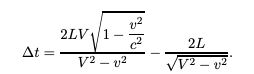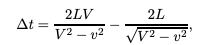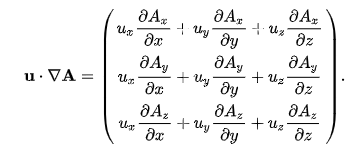The victorious truther

I'd like to point out that in lieu of modern spacetime formalisms and mathematical knowledge it is also the case that even in a classical context that gravity should be treated as a force could be considered dubious. Versions of Newton-Cartan gravity exist which is basically a geometrical realization of classical gravitation or, if you are avoidant of such terminology, is a version of newtonian gravitation/Classical physics in which what an inertial reference frame is or what path they follow is found to be dependent on the local/global mass distributions. So if you placed an object at rest or give it some initial velocity it wouldn't remain at rest or follow merely a straight line but a curved one in the presence of some mass distribution while all local experiments would convince you as to it being an inertial reference. Do note that together with the curvature based formulation of General Relativity there is also a version of General Relativity known as tele-parallel gravity that would replicate most if not all of General Relativities predictions but seems to appear to be a force field. This is done by assuming that the curvature is absent from determining the interaction and rather its the torsion (how much your world line bends) in spacetime that determines how the gravitational interaction takes place. So, is gravity then a force once again? As was showcased in the first paragraph in the classical situation perhaps this is all but arbitrary and what you are really looking for has less to do with force. Perhaps, it has more to do with what you consider to be inertial or non-inertial and how much you're willing to apply occam's razor.

I've been, as of late, debating with rather fringe or crackpot physicists on ResearchGate and in the process of such an exchange i've found myself forced to be rather particular about my terminology. It was a debate regarding Special Relativity and the person in question made the obvious mistake of assuming that such a theory couldn't be extended to accelerating reference frames. I came to clarify to him that in Special Relativity you could only deal with reference frames that accelerate as a result of dynamical influences or forces as General Relativity would come into the case for accelerated motions without forces. In hindsight, it is relatively true this is the case in so much as General Relativity accounts for everything that Special Relativity could account for as well as much more. However, I came to later realize in some respect that, in a similar manner to Classical mechanics, a fictitious forces would arise in any non-inertial reference frame I extend Special Relativity to so therefore it should equally as much handle it as well. Then it occurred to me; the definition of an inertial reference frame or the general intuition many have had through out our physics history, from Galileo to Newton and then to Einstein's statement of it in his 1905 paper, all seemed to implicitly assume that for constant velocity motion the fact of it being an inertial frame came whole sale. In an opposite manner when discussing accelerating frames these are usually thrown into the bin of non-inertial frames as well. However, there are cases that do not relegate this sort of strict intuitive dichotomy in that you can view accelerated inertial frames from a non-inertial reference frame (linearly or in rotational motion) and such that the people outside the non-inertial frame will claim that their laws of physics remained valid despite this relative acceleration you perceived. Its as if the definition of an inertial frame that includes not just the statement of the invariance of some collection of laws of physics but also of a constant velocity has exceptions that do not warrant such a strict adherence to only constant relative velocities. Even Newton proclaimed in a strangely familiar manner in Corollary 6 of his Principia that, Then the question arises as to why we prefer to distinguish two different frames of reference where one is part of a homogeneous influence of forces (non-inertial) and the other is inertial (perceived from the other frame to be accelerated) when the physics conspires to not have us distinguish them. It seems then that you can extend this argument to any magnitude of homogeneous forces or any dependency on direction/magnitude, so long as its homogeneous, such that any general kinematical motion could be further relegated also to being inertial. It seems to be fairly redundant and i'm curious if Newton or others ever attempted to specify why inertial reference frames were so relegated usually to only constant velocities if they even noticed these sorts of equivalent situations. For Newton's own gravitational theory this relativization and treatment of 'gravitationally' accelerated motion can be performed creating a Classical geometrical version of Newtonian gravitation called Newton-Cartan gravity. Entirely from arguments based on the above corollary along with assumptions regarding the WEP and SEP (Weak and strong gravitational equivalence principles). You don't have to see it as the inclusion then of a warped spacetime but merely as a redefinition and generality of inertial frames that responds to corollary 6 by making all such equivalent frames a part of the definition of being inertial. This is a curiosity to my Classical intuitions as they have always then betrayed me into thinking about constant velocity inertial motion as a strict given when these exceptions screamed for Occam's razor to be applied to them. Perhaps an approach that emphasizes the relativity of inertial frames in many cases, as is the case here, would be more amenable in certain teaching settings for a gentler transition from Special Relativity into General Relativity which wouldn't be too distinct in core concepts when going from Newtonian gravitation to Newton-Cartan theory. The key point being that kinematical motions are somewhat of a byproduct of being inertial or non-inertial and may be sometimes necessary but not sufficient to make a distinction between them. What are your thoughts?

I'm fairly unfamiliar with data processing and data analysis in astrophysics so i'm unsure how to address certain claims as to the veracity of astronomical measurements. The paper by a crank physicist named Pierre-Marie Robitaille got me thinking. What is a respectable signal to noise ratio in astrophysics and, in particular, why a ratio of less than 2:1 for the Wmap data could be then considered an accurate recording of the CMB? What could be considered a standard in astrophysics for a signal to noise ratio that would indicate an accurate reading? If you could supply some extra reading material at the undergraduate level i'd appreciate it. 802260431_PierrePaper.pdf

So i've been arguing with someone on ResearchGate regarding Special Relativity and other caveats related to his own pet Aether theory. He is, as many of these non-mainstream critics of Special Relativity are, a big fan of specific interferometer results from the late nineteenth or early twentieth century as he supports his theory on the back of a re-analysis of previous results. He claims that any vacuum interferometer will give a null result and that interferometers with a medium for the light beams would then give a non-null result. Something that was analyzed in this paper here: https://arxiv.org/pdf/physics/0205070.pdf. I'm curious about what your perspectives on it are given the derivations from their initial assumptions seemed to check out. If you could find a resource(s) for Lorentz Violating experiments conducted in a medium i'd heavily appreciate that. I had found a few that I thought had a relation to this such as https://arxiv.org/abs/0706.2031v1. His own paper is given here: https://www.researchgate.net/publication/350770907_MM-Cahill The key idea is that this analysis combines both Lorentz contraction and the idea of light having a different speed in a chosen medium of \[ V = \frac{c}{n} .\] You basically then perform the same analysis to determine the time difference between a path in the direction of motion and the path of the interferometer arm perpendicular to that. Which comes out to be Compared to it without the Lorentz contraction taken into account

I got the second equation wrong when I expanded it out. It should look like that. 🙁

Well, the density distribution could be discontinuous and the idea here is that there are so many innumerable masses i'm thinking you could model it as an evolving non-interacting continuum of sorts (aside from gravitational interactions). Sort of like how we have equations to deal with individual H2O molecules and perhaps also a handful of them but as you increase the number of them then at some point you could fairly well approximate it by throwing out the assumption of a discretized fluid. Then model the fluid continuously with the Naviar-Stokes equations. I'm hoping the same can be done with a density distribution of sorts. Further, at the moment i'm just thinking of directly doing it in the source code.

I'm most importantly wondering if this system of PDE's correctly describe exactly what i'm trying to model. Simulation of matter moving around while not interacting with itself aside from being gravitationally attractive. No mass accumulation or other non-gravitational forces present. No mass sinks or sources.

\[ \begin{bmatrix} 4 \\ 5 \end{bmatrix} + \]

Dear forum, So I was curious about methods through which to simulate gravitational interactions and while I know there are numerous methods through which to numerically deal with multiple individual bodies I decided to find one to deal with general mass distributions. The model in question having ignore their interactions through non-gravitational forces or add in any accumulation of mass (formation of planetesimals) but still account for the change in the density distribution as well as the distribution of velocities. Firstly the primary equation in question that would be used is gauss law of gravitation to calculate the current gravitational potential distribution from the density distribution. Then i'd need an equation to encapsulate the conservation of mass to help with designating what the next distribution of matter would be. Finally, i'll need one more to determine the next velocity distribution and then repeat the whole process. I sort of guessed at this and found this set of PDE's that would suit my interest; gathered from continuum mechanics. 1) \( \nabla^{2} \phi = 4 \pi G \rho \) 2) \( \frac{\partial \vec{u}}{\partial t} + \vec{u} \cdot \nabla \vec{u} = - \nabla \phi \) 3) \( \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec{u}) =0 \) The first is gauss law for gravity then the second is basically newtons second law but with a total derivative with the mass canceled out because of the weak equivalence principle (also because of mass conservation it takes on that form). The third and final equation is basically just a statement of mass conservation. I attempted to go on through and write these out full sale to then later discretize them or apply some other finite difference scheme to put into some programmable format using scipy, python, numpy, etc. These forms are given below, 1) \( \frac{\partial^{2} \phi}{\partial x^{2}} + \frac{\partial^{2} \phi}{\partial y^{2}} + \frac{\partial^{2} \phi}{\partial z^{2}} = 4 \pi G \rho \) 2) \[ \begin{bmatrix} \frac{\partial u_{x}}{\partial t} \\ \frac{\partial u_{y}}{\partial t} \\ \frac{\partial u_{z}}{\partial t} \end{bmatrix} + \begin{bmatrix} u_{x} \frac{\partial u_{x}}{\partial x} + u_{y} \frac{\partial u_{y}}{\partial x} + u_{z} \frac{\partial u_{z}}{\partial x} \\ u_{x} \frac{\partial u_{x}}{\partial y} + u_{y} \frac{\partial u_{y}}{\partial y} + u_{z} \frac{\partial u_{z}}{\partial y} \\ u_{x} \frac{\partial u_{x}}{\partial z} + u_{y} \frac{\partial u_{y}}{\partial z} + u_{z} \frac{\partial u_{z}}{\partial z} \end{bmatrix} + \begin{bmatrix} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \] 3) \( \frac{\partial \rho}{\partial t} + u_{x} \frac{\partial \rho}{\partial x} + u_{y} \frac{\partial \rho}{\partial y} + u_{z} \frac{\partial \rho}{\partial z} + \rho \frac{\partial u_{x}}{\partial x} + \rho \frac{\partial u_{y}}{\partial y} + \rho \frac{\partial u_{z}}{\partial z}= 0 \) Any assistance in terms of implementing these or stable numerical methods would be highly appreciated.

Are all decays in QM or QF mediated by the weak force?

Aware in the same sense that you sitting in a chair makes you and the chair 'aware' of each other. I should have used a word like 'interaction'. In Quantum Mechanics or Quantum Field theory what theoretical entities are mean't to bring about the decay of a muon?

Why does it have to? You are anthropomorphizing this. In special relativity we assume that certain objects have their own respective proper time and i'm assuming this translates over to QM as well as QF. Is it arbitrary when it decays then and how long afterwards? If not, then how does it know when it should be more probable to decay versus when it should if it can't keep track of how long it has been existent? Does it not have its own sense of proper time in Quantum Field theory or Quantum Mechanics? I'd be anthropomorphizing this if I said the muon must have a top hat and a pocket watch.

The muon is not in the absence of changes or in this case if we assume its monadic properties are retained across time (via a physical instrument) it would be wrong to say it doesn't undergo or is absent from any change at all. Relational change (relative velocity), that is, not a change in its monadic properties (though how we would know its monadic properties didn't change is a tricky one). I'm not entirely saying that its relational changes cause it to decay but they do influence it (relative speed to other frames of reference). All of this is in the end is taking for granted the muons own clock and its proper time of which i'm not sure we've investigated. . . how does a muon keep track of time internally? This may be your thread, but your latest post moves the goalposts. Before you can discuss time in universes we are not in, you have to prove that the time in these universes is the same as time in out universe. Difficult since we have not yet arrived at a definition of time in our universe. Sorry. . . I was just playing a bit loose there with the terminology and positions from a sort of naive perspective.

There is no centrifugal force when seen from your inertial frame of reference.

At some point the whole thing is at rest then at a later time it's moving at a constant linear and angular velocity with respect to its center of mass. Thusly, there wasn't actually any conservation of angular momentum or energy because work was done (in this case both linear as well as rotational work). Energy was not in fact conserved if this bolt went from not moving to moving. If you are truly to do this correctly you CANNOT be ignorant to what frame of reference you are in whether inertial or in the rotating frame of reference. Further, fully analyze it from the inertial frame of reference then move into the non-inertial one with mathematics to back up your conclusions.