Duda Jarek
Senior Members-
Posts
572 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by Duda Jarek
-
Regarding neutrinos, I haven't heard of suspicion that they might violate CPT? Regarding baryogenesis as violation of baryon number conservation, it is a hypothetical process and could be avoided if assuming Big Bounce: maintaining fixed number of baryons before and after. Assuming baron number can be violated, baryons should be also possible to destroy (as in proton decay) e.g. in Big Crunch, they are also hypothesized to be destroyed in Hawking radiation: effectively transforming matter into massless radiation.
-
While CPT theorem suggests that all processes have time/CPT-symmetric analogues, there are popular doubts regarding some - starting with measurement: 1) Example of wavefunction collapse is atom deexcitation, releasing energy - it is reversible, but it requires providing energy e.g. in form of photon to excite back an atom. Can measurement be seen this way - that there is always some accompanying process like energy release, which would need to be also reversed? For example in Stern-Gerlach experiment: spin tilting to parallel or anti-parallel alignment to avoid precession in strong magnetic field - does it have some accompanied process like energy release e.g. as photon? Can it be observed? 2) Another somehow problematic example is stimulated emission used in laser - causing photon emission, which finally e.g. excites a target, later by light path. Does it have [urlhttps://physics.stackexchange.com/questions/308106/causality-in-cpt-symmetry-analogue-of-free-electron-laser-stimulated-absorbtion]time/CPT-symmetric analogue[/url]: some stimulated absorption - causing photon absorption, which e.g. deexcites a target, earlier by light path? 3) Quantum algorithms usually start with state preparation: all 0/1 qubits are initially fixed to let say <0|. Could there be time/CPT analogue of state preparation: fixing values but at the end (as |0>)? 4) One of cosmological examples is Big Bang: which hypothesis of the point of start of time seems in disagreement with CPT theorem - instead suggesting some symmetric twin of Big Bang before it, like in cyclic model of universe. Is hypothesis of the point of start of time in agreement with CPT theorem? Could these two possibilities be distinguished experimentally? What other processes are seen as problematic from time/CPT symmetry perspective? Which can be defended, and which essentially require some fundamental asymmetry?
-

Immunity by incompatibility – hope in chiral life
Duda Jarek replied to Duda Jarek's topic in Biology
I don't doubt that free-cell synthesis can get high production ... assuming you have a good source of e.g. polymerase, which are the real problem here - without mirror cells and ribosomes ... Beside industrial applications, mirror life will be also a crucial milestone in development of synthetic life - the first really different and reasonable (in contrast to e.g. additional nucleotides), and natural development will make it in reach in a few decades, e.g.: 2002 - synthetic virus: https://en.wikipedia.org/wiki/Synthetic_virology 2010 - synthetic cell: https://en.wikipedia.org/wiki/Artificial_cell#Synthetic_cells 2013 - synthetic ribosome: https://en.wikipedia.org/wiki/Synthetic_ribosome 2016 - large mirror protein (polymerase) Will we be really able to contain it then forever? - with human factors, antibiotics resistance, accidents, etc. ... it seems a matter of time when it will finally reach natural environment and start searching an ecological niche to populate, evolve, diversify ... -

Immunity by incompatibility – hope in chiral life
Duda Jarek replied to Duda Jarek's topic in Biology
I don't have education in biochemistry (physics, cs, math), but it seems highly unlikely that you could produce macroscopic (e.g. grams) amounts of large molecules this way (?) Especially proteins requiring mirror ribosomes, often complex post processing, help in folding ... Cell-free synthesis might be useful for extremely rare diseases, but finding some promising drug for a common disease in this huge mirror world, there would be needed kilograms, tonnes to synthesize - what is completely unrealistic without mirror life ... which should become easier every year due to natural development of technology. Anyway, I think it is a matter of time (less than a century) when, due to ambition/money incentives/"because we can", somebody will open this Pandora box, e.g. secretly in a lab in China like for CRISPR babies ... -

Immunity by incompatibility – hope in chiral life
Duda Jarek replied to Duda Jarek's topic in Biology
Hello, the Nature article mentions aptamers as direct application, which are length 30-80 oligonucleotides. Enantiomers of the small ones probably can be directly synthesized in negligible quantity. Now they have mirror polymerase allowing to speed it up, but being relatively costly to synthesize, how many copies can produce a single molecule of polymerase? For mass production there is needed mirror life. And aptamers are just the beginning - mirror life would literally double the space of possible large molecules we can mass produce. Starting actively searching this space, we can find many valuable ones. Especially enzymes - complex and effective nanomachines, optimized for very sophisticated tasks. Anyway, there are extremely strong incentives, not only financial, to go toward finally synthesizing mirror life - like CRISPR babies, there might be no way to stop it (?) What we can do is trying to prepare - understand it well, try to protect from the dangers. And there are many of them - earlier than mirror cyanobacteria dominating our ecosystem due to less prepare natural enemies, potentially killing us all in a few centuries. Bacteria has extremely fast evolution - already can consume l-sugars, and can quickly adapt to others. Mirror E. Coli might already find unusual ecological niches, disturbing ecosystem in an unpredictable way. I wouldn't be surprised if synthesizing mirror life was a factor in Fermi paradox - it is a natural possibility in development of civilization ... which might lead to its extermination. -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
studiot, according to Wikipedia, Earnshaw's theorem says "that a collection of point charges cannot be maintained in a stable stationary equilibrium configuration solely by the electrostatic interaction of the charges" ... while here we are talking about configuration of EM field of a single electron. Regarding " Or are you claiming that non tunneling electrons do not have a wavefunction that extends beyond their situs? " - no, by "on average" I mean that you can translate this wavefunction into probability to answer the question of size of electron, e.g. a radius such that half of 511keVs energy is on average in this radius around the center of electron. swansont, if you want to relate radius of electron to its electric dipole moment ... why not to use magnetic dipole instead? - which is huge. If you are able to defend Dehmelt's g-factor argument I would be really interested. It looks like at first he extrapolated with line, getting negative radius for electron - so he has chosen parabola to get exactly 0 radius for g=2, what is "proving" by assuming the thesis. Also, we have more 3-parton particles, like neutron, which RMS radius is negative due to minuses being further than pluses ... For fundamental particles we cannot talk about RMS radius, but we can about differences from (infinite energy) EM field configuration of perfect point charge. -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
As written, I have returned to this topic due to Neumaier's page with many materials: https://www.mat.univie.ac.at/~neum/physfaq/topics/pointlike.html But generally the fundamental question of size of electron remains unanswered - while there are many suggestions of femtometer-scale size of electron (as deformation from perfect point charge), I still haven't seen any real (not fitting parabola to two point) arguments that it is essentially smaller (claimed e.g. in Wikipedia). -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
studiot, quantum formalism can be translated into probabilities with Born rule - while we cannot ask about exact e.g. position, QM still allows to ask about its expected value: "on average". swansont, looking at electron-positon scattering cross section as one of suggestions, it includes all their interactions. Electron's 511keV energy is at least partially distributed into energy of fields of interactions: probably mainly EM. Still we don't know this distribution (even average), naive assumption of perfect point would mean infinite energy. So what is this configuration of EM field near the center of electron? E.g. in ball of what radius there is half of this energy? (on average) -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
Ok, you can say that there are some quantum or statistical fluctuations ... I can respond with just adding "on average". For example: ball of which radius contains on average half of 511keVs energy of electron? Is it femtomer-scale radius, or much smaller? -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
Generally, we are interested in size of rest electron, not of squeezed electron. There are some complex dependencies from its squeezing with Lorentz contraction - we need to remove them, e.g. by extrapolating to rest energy (any other ways?) A general question regards distribution of electron's 511keVs energy - some of it is in energy of electric field (... infinite assuming perfect point), some could be e.g. in energy of fields related to other interactions electron takes part: gravitational, weak ... So e.g. ball of which radius contains half of 511keVs energy of electron? Is it femtomer-scale radius, or much smaller? -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
Arnold Neumaier has responded on stack ( https://physics.stackexchange.com/questions/397022/experimental-boundaries-for-size-of-electron ) - he has gathered many materials on this topic: https://www.mat.univie.ac.at/~neum/physfaq/topics/pointlike.html But still no clear argument that electron is much smaller then femtometer (?) Anyway, to better specify the problem, define E(r) as energy in a radius r ball around electron. We know that E(r) ~ 511keVs for large r, for smaller it reduces e.g. by energy of electric field. Assuming perfect point charge, we would get E(r) -> -infinity for r->0 this way. Where does divergence from this assumption starts? More specifically: for example where is maximum of E'(r) - in which distance there is maximal deposition of 511keVs energy? Or median range: such that E(r) = 511/2 keVs. It is not a question about the exact values, only their scale: ~femtometer or much lower? -

How quantum is wave-particle duality of Couder's walking droplets?
Duda Jarek replied to Duda Jarek's topic in Physics
Sure, it misses a lot from real physics, like it seems impossible to model 3D this way, also clock here is external while in physics it is rather internal of particles (de Broglie's, zitterbewegung): https://physics.stackexchange.com/questions/386715/does-electron-have-some-intrinsic-1021-hz-oscillations-de-broglies-clock But these hydrodynamical analogues provide very valuable intuitions about the real physics ... -

How quantum is wave-particle duality of Couder's walking droplets?
Duda Jarek replied to Duda Jarek's topic in Physics
Oh, muuuch more has happened - see my slides with links to materials: https://www.dropbox.com/s/kxvvhj0cnl1iqxr/Couder.pdf Interference in particle statistics of double-slit experiment (PRL 2006) - corpuscle travels one path, but its "pilot wave" travels all paths - affecting trajectory of corpuscle (measured by detectors). Unpredictable tunneling (PRL 2009) due to complicated state of the field ("memory"), depending on the history - they observe exponential drop of probability to cross a barrier with its width. Landau orbit quantization (PNAS 2010) - using rotation and Coriolis force as analog of magnetic field and Lorentz force (Michael Berry 1980). The intuition is that the clock has to find a resonance with the field to make it a standing wave (e.g. described by Schrödinger's equation). Zeeman-like level splitting (PRL 2012) - quantized orbits split proportionally to applied rotation speed (with sign). Double quantization in harmonic potential (Nature 2014) - of separately both radius (instead of standard: energy) and angular momentum. E.g. n=2 state switches between m=2 oval and m=0 lemniscate of 0 angular momentum. Recreating eigenstate form statistics of a walker's trajectories (PRE 2013). In the slides there are also hydrodynamical analogous of Casimir and Aharonov-Bohm. -
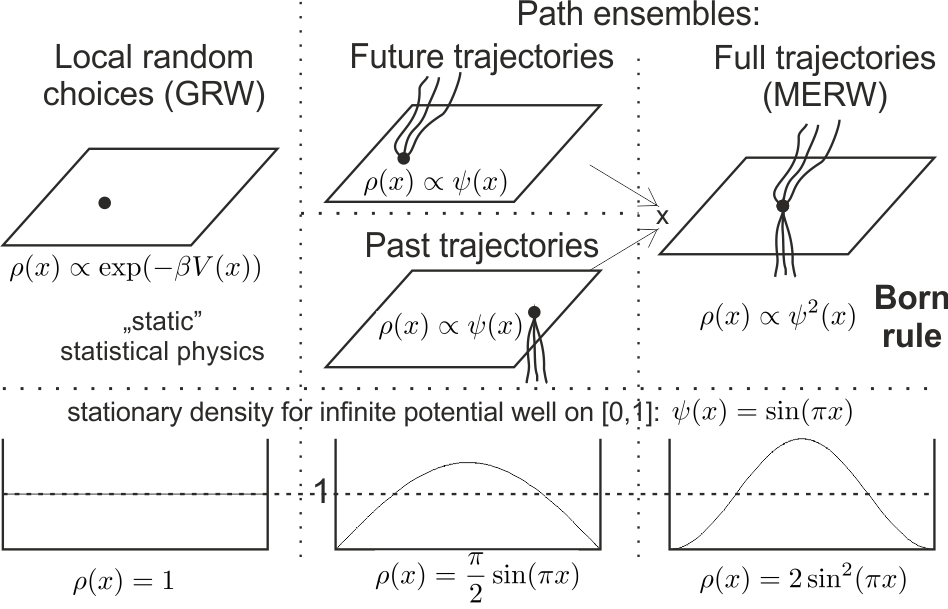
While the original Bell inequality might leave some hope for violation, here is one which seems completely impossible to violate - for three binary variables A,B,C: Pr(A=B) + Pr(A=C) + Pr(B=C) >= 1 It has obvious intuitive proof: drawing three coins, at least two of them need to give the same value. Alternatively, choosing any probability distribution pABC among these 2^3=8 possibilities, we have: Pr(A=B) = p000 + p001 + p110 + p111 ... Pr(A=B) + Pr(A=C) + Pr(B=C) = 1 + 2 p000 + 2 p111 ... however, it is violated in QM, see e.g. page 9 here: http://www.theory.caltech.edu/people/preskill/ph229/notes/chap4.pdf If we want to understand why our physics violates Bell inequalities, the above one seems the best to work on as the simplest and having absolutely obvious proof. QM uses Born rules for this violation: 1) Intuitively: probability of union of disjoint events is sum of their probabilities: pAB? = pAB0 + pAB1, leading to above inequality. 2) Born rule: probability of union of disjoint events is proportional to square of sum of their amplitudes: pAB? ~ (psiAB0 + psiAB1)^2 Such Born rule allows to violate this inequality to 3/5 < 1 by using psi000=psi111=0, psi001=psi010=psi011=psi100=psi101=psi110 > 0. We get such Born rule if considering ensemble of trajectories: that proper statistical physics shouldn't see particles as just points, but rather as their trajectories to consider e.g. Boltzmann ensemble - it is in Feynman's Euclidean path integrals or its thermodynamical analogue: MERW (Maximal Entropy Random Walk: https://en.wikipedia.org/wiki/Maximal_entropy_random_walk ). For example looking at [0,1] infinite potential well, standard random walk predicts rho=1 uniform probability density, while QM and uniform ensemble of trajectories predict different rho~sin^2 with localization, and the square like in Born rules has clear interpretation: Is ensemble of trajectories the proper way to understand violation of this obvious inequality? Comparing with local realism from Bell theorem, path ensemble has realism and is non-local in standard "evolving 3D" way of thinking ... however, it is local in 4D view: spacetime, Einstein's block universe - where particles are their trajectories. What other models with realism allow to violate this inequality?
- 1 reply
-
1
-

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
Sure, it isn't - fm size is only a suggestion, but a general conclusion here is that cross section does not offer a sub-femtometer boundary for electron size (?) Dehmelt's argument of fitting parabola to 2 points: so that the third point is 0 for g=2 ... is "proof" of tiny electron radius by assuming the thesis ... and at most criticizes electron built of 3 smaller fermions. So what experimental evidence bounding size of electron do we have? -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
Sure, so here is the original Cabbibo electro-positron collision 1961 paper: https://journals.aps.org/pr/abstract/10.1103/PhysRev.124.1577 Its formula (10) says sigma ~ \beta/E^2 ... which extrapolation to resting electron gives ~ 2fm radius. Indeed it would be great to understand corrections to potential used in Schrodinger/Dirac, especially for r~0 situations like electron capture (by nucleus), internal conversion or positronium. Standard potential V ~ 1/r goes to infinity there, to get finite electric field we need to deform it in femtometer scale -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
Could you give some number? Article? We can naively interpret cross-section as area of particle, but the question is: cross-section for which energy should we use for this purpose? Naive extrapolation to resting electron (not Lorentz contracted) suggests ~2fm electron radius this way (which agrees with size of needed deformation of electric field not to exceed 511 keVs energy). Could you propose some different extrapolation? -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
So can you say something about electron size based on electron-positron cross section alone? -

Experimental boundaries for size of electron?
Duda Jarek replied to Duda Jarek's topic in Modern and Theoretical Physics
No matter interpretation, if we want boundaries for size of electron, it shouldn't be calculated for Lorentz contracted electron, but for resting electron - extrapolate above plot to gamma=1 ... or take direct values: So what boundary for size of (resting) electron can you calculate from cross-sections of electron-positron scattering? -
There is some confidence that electron is a perfect point e.g. to simplify QFT calculations. However, searching for experimental evidence (stack), Wikipedia article only points argument based on g-factor being close to 2: Dehmelt's 1988 paper extrapolating from proton and triton behavior that RMS (root mean square) radius for particles composed of 3 fermions should be ~g-2: Using more than two points for fitting this parabola it wouldn't look so great, e.g. neutron (udd) has g~ -3.8, \(<r^2_n>\approx -0.1 fm^2 \) And while classically g-factor is said to be 1 for rotating object, it is for assuming equal mass and charge density. Generally we can classically get any g-factor by modifying charge-mass distribution: \[ g=\frac{2m}{q} \frac{\mu}{L}=\frac{2m}{q} \frac{\int AdI}{\omega I}=\frac{2m}{q} \frac{\int \pi r^2 \rho_q(r)\frac{\omega}{2\pi} dr}{\omega I}= \frac{m}{q}\frac{\int \rho_q(r) r^2 dr}{\int \rho_m(r) r^2 dr} \] Another argument for point nature of electron is tiny cross-section, so let's look at it for electron-positron collisions: Beside some bumps corresponding to resonances, we see a linear trend in this log-log plot: 1nb for 10GeVs (5GeV per lepton), 100nb for 1GeV. The 1GeV case means \(\gamma\approx1000\), which is also in Lorentz contraction: geometrically means gamma times reduction of size, hence \(\gamma^2\) times reduction of cross-section - exactly as in this line on log-log scale plot. More proper explanation is that it is for collision - transforming to frame of reference where one particle rests, we get \(\gamma \to \approx \gamma^2\). This asymptotic \(\sigma \propto 1/E^2\) behavior in colliders is well known (e.g. (10) here) - wanting size of resting electron, we need to take it from GeVs to E=511keVs. Extrapolating this line (no resonances) to resting electron (\(\gamma=1\)), we get 100mb, corresponding to ~2fm radius. From the other side we know that two EM photons having 2 x 511keV energy can create electron-positron pair, hence energy conservation doesn't allow electric field of electron to exceed 511keV energy, what requires some its deformation in femtometer scale from \(E\propto1/r^2 \): \[ \int_{1.4fm}^\infty \frac{1}{2} |E|^2 4\pi r^2 dr\approx 511keV \] Could anybody elaborate on concluding upper bound for electron radius from g-factor itself, or point different experimental boundary? Does it forbid electron's parton structure: being "composed of three smaller fermions" as Dehmelt writes? Does it also forbid some deformation/regularization of electric field to a finite energy?
-

Four-dimensional understanding of quantum computers
Duda Jarek replied to Duda Jarek's topic in Quantum Theory
Thanks, I would gladly discuss. The main part of the paper is MERW ( https://en.wikipedia.org/wiki/Maximal_Entropy_Random_Walk) showing why standard diffusion has failed (e.g. predicting that semiconductor is a conductor) - because it has used only an approximation of the (Jaynes) principle of maximum entropy (required by statistical physics), and if using the real entropy maximum (MERW), there is no longer discrepancy - e.g. its stationary probability distribution is exactly as in the quantum ground state. In fact MERW turns out just assuming uniform or Boltzmann distribution among possible paths - exactly like in Feynman's Eulclidean path integrals (there are some differences), hence the agreement with quantum predictions is not a surprise (while still MERW being just a (repaired) diffusion). Including the Born rule: probabilities being (normalized) squares of amplitudes - amplitude describes probability distribution at the end of half-paths toward past or future in Boltzmann ensemble among paths, to randomly get some value in a given moment we need to "draw it" from both time directions - hence probability is square of amplitude: Which leads to violation of Bell inequalities: top below there is derivation of simple Bell inequality (true for any probability distribution among 8 possibilities for 3 binary variables ABC), and bottom is example of their violation assuming Born rule: -

Four-dimensional understanding of quantum computers
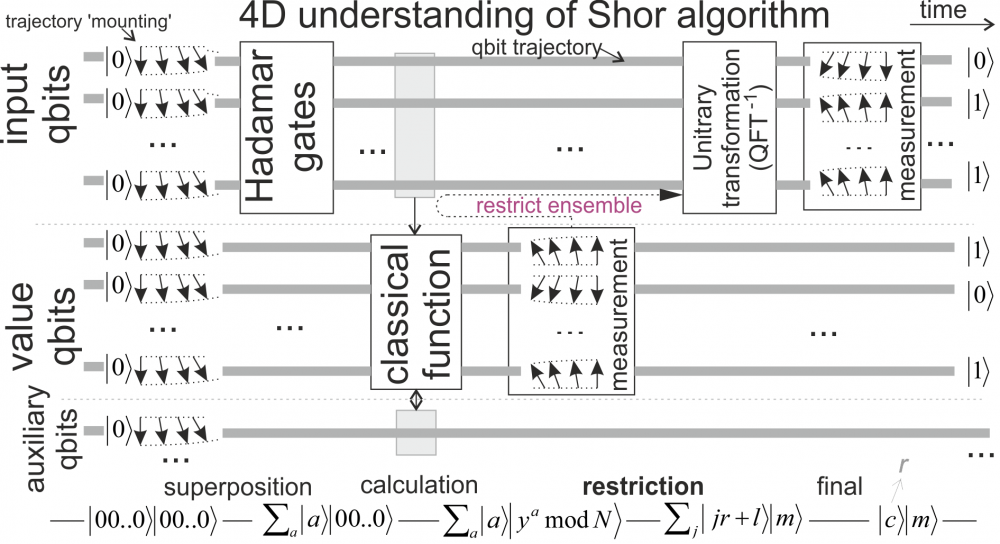
Duda Jarek replied to Duda Jarek's topic in Quantum Theory
After 7 years I have finally written it down: https://arxiv.org/pdf/0910.2724v2.pdf Also other consequences of living in spacetime, like violation of Bell inequalities. Schematic diagram of quantum subroutine of Shor's algorithm for finding prime factors of natural number N. For a random natural number y<N, it searches for period r of f(a)=y^a mod N, such period can be concluded from measurement of value c after Quantum Fourier Transform (QFT) and with some large probability (O(1)) allows to find a nontrivial factor of N. The Hadamar gates produce state being superposition of all possible values of a. Then classical function f(a) is applied, getting superposition of |a> |f(a)>. Due to necessary reversibility of applied operations, this calculation of f(a) requires use of auxiliary qbits, initially prepared as |0>. Now measuring the value of f(a) returns some random value m, and restricts the original superposition to only a fulfilling f(a)=m. Mathematics ensures that {a:f(a)=m} set has to be periodic here (y^r \equiv 1 mod N), this period r is concluded from the value of Fourier Transform (QFT). Seeing the above process as a situation in 4D spacetime, qbits become trajectories, state preparation mounts their values (chosen) in the past direction, measurement mounts their values (random) in the future direction. Superiority of this quantum subroutine comes from future-past propagation of information (tension) by restricting the original ensemble in the first measurement. -

Immunity by incompatibility – hope in chiral life
Duda Jarek replied to Duda Jarek's topic in Biology
A decade has passed, moving this topic from SF to synthetic life: https://en.wikipedia.org/wiki/Chiral_life_concept One of the most difficult tasks seemed to be able to synthesize working proteins ... and last year Chinese have synthesized mirror polymeraze: Nature News 2016: Mirror-image enzyme copies looking-glass DNA, Synthetic polymerase is a small step along the way to mirrored life forms, http://www.nature.com/news/mirror-image-enzyme-copies-looking-glass-dna-1.19918 There are also lots of direct economical motivations to continue to synthesize mirror bacteria, like for mass production of mirror proteins (e.g. aptamers) or L-glucose (perfect sweetener). So in another decade we might find out that a colony of mirror bacteria is already living e.g. in some lab in China ... ... taking us closer to a possibility nicely expressed in the title of WIRED 2010 article: "Mirror-image cells could transform science - or kill us all" ( https://www.wired.com/2010/11/ff_mirrorlife/ ) - estimating that it would take a mirror cyanobacteria (photosynthesizing) a few centuries to dominate our planet ... eradicating our life ... -
There is a recent article in a good journal (Optics July 2015) showing violation of Bell inequalities for classical fields: "Shifting the quantum-classical boundary: theory and experiment for statistically classical optical fields" https://www.osapublishing.org/optica/abstract.cfm?URI=optica-2-7-611 Hence, while Bell inequalities are fulfilled in classical mechanics, they are violated not only in QM, but also classical field theories - asking for field configurations of particles (soliton particle models) makes sense. It is obtained by superposition/entanglement of electric field in two directions ... analogously we can see a crystal through classical oscillations, or equivalently through superposition of their normal modes: phonos, described by quantum mechanics, violating Bell inequalities.
-
Regarding Bell - we know that nature violates his inequalities, so we need to find an erroneous assumption in his way of thinking. Let's look at a simple proof from http://www.johnboccio.com/research/quantum/notes/paper.pdf So let us assume that there are 3 binary hidden variables describing our system: A, B, C. We can assume that the total probability of being in one of these 8 possibilities is 1: Pr(000)+Pr(001)+Pr(010)+Pr(011)+Pr(100)+Pr(101)+Pr(110)+Pr(111)=1 Denote by Pe as probability that given two variables have equal values: Pe(A,B) = Pr(000) + Pr (001) + Pr(110) + Pr(111) Pe(A,C) = Pr(000) + Pr(010) + Pr(101) + Pr(111) Pe(B,C) = Pr(000) + Pr(100) + Pr(011) + Pr(111) summing these 3 we get Bell inequalities: Pe(A,B) + Pe(A,C) + Pe(B,C) = 1 + 2Pr(000) + 2 Pr(111) >= 1 Now denote ABC as outcomes of measurement in 3 directions (differing by 120 deg) - taking two identical (entangled) particles and asking about frequencies of their ABC outcomes, we can get Pe(A,B) + Pe(A,C) + Pe(B,C) < 1 what agrees with experiment ... so something is wrong with the above line of thinking ... The problem is that we cannot think of particles as having fixed ABC binary values describing direction of spin. We can ask about these values independently by using measurements - which are extremely complex phenomena like Stern-Gerlach. Such measurement doesn't just return a fixed internal variable. Instead, in every measurement this variable is chosen at random - and this process changes the state of the system. Here is a schematic picture of the Bell's misconception: The squares leading to violation of Bell inequalities come e.g. from completely classical Malus law: the polarizer reduces electric field like cos(theta), light intensity is E^2: cos^2(theta). http://www.physics.utoronto.ca/~phy225h/experiments/polarization-of-light/polar.pdf To summarize, as I have sketched a proof, the following statement is true: (*): "Assuming the system have some 3 fixed binary descriptors (ABC), then frequencies of their occurrences fulfill Pe(A,B) + Pe(A,C) + Pe(B,C) >= 1 (Bell) inequality" Bell's misconception was applying it to situation with spins: assuming that the internal state uniquely defines a few applied binary values. In contrast, this is a probabilistic translation (measurement) and it changes the system. Beside probabilistic nature, while asking about all 3, their values would depend on the order of questioning - ABC are definitely not fixed in the initial system, what is required to apply (*).