Duda Jarek

Indeed "baryons -> black hole -> massless Hawking radiation" could be one way to realize stimulated proton decay ... but if this one is possible, there might be also other e.g. more direct ways, like using sequence of laser pulses to directly "swing out" proton from local minimum field configuration.

I was thinking about even more SF ultimate power source: stimulated proton decay - nearly complete matter -> energy transition, ~100x higher energy density than fusion from any matter. While they search for proton decay in room temperature water pools, it is hypothesized e.g. for baryongenesis (more matter than antimatter just after Big Bang), or Hawking radiation (baryons -> black hole -> massless radiation) - situations with extreme conditions, so I would search for it e.g. in the centers of neutron stars just before collapse to black hole, colliders like LHC (to test if it happens would need a dedicated experiment). E.g. to explain orders of magnitudes brighter objects than allowed by standard explanations like "Bizarre object 10 million times brighter than the sun defies physics, NASA says" from https://www.space.com/bizare-object-10-times-brighter-than-sun If possible, it would mean proton is a very deep but local minimum of field configuration - maybe it could be "swing out" of this minimum e.g. with some precise sequence of laser pulses?

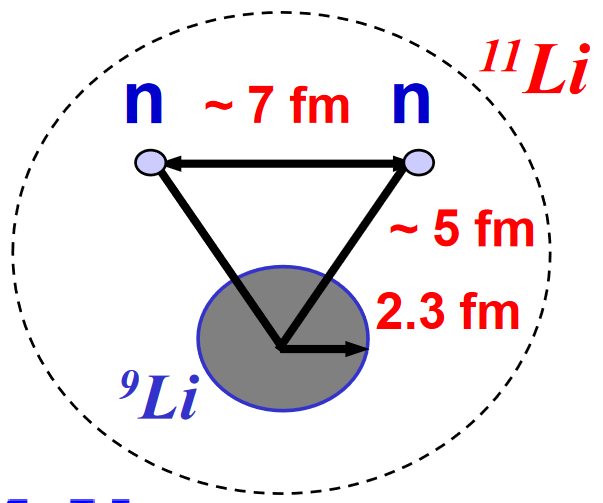
In halo nuclei there are stably (milliseconds) bind neutrons/protons in much larger distances ... but we are still talking about a few femtometers. https://en.wikipedia.org/wiki/Halo_nucleus http://theor.jinr.ru/~ntaa/17/files/lectures/Ershov.pdf

Being able to build gamma laser ( https://en.wikipedia.org/wiki/Gamma-ray_laser ), fusion could be trivial - e.g. 782 keV photons to reverse neutron decay: producing free neutrons from hydrogen. However, it is technically extremely difficult, for free electron lasers maybe 30keV might be reachable, here is 14.4keV for nuclear transition: https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.L032007

Talk about such potential more symmetric enhancement of quantum computers allowing to attack NP problems ( https://arxiv.org/pdf/2308.13522 , slides ) :

Separate paper about such 2WQC: https://www.researchgate.net/publication/372677599_Two-way_quantum_computers_adding_CPT_analog_of_state_preparation As stimulated emission-absorption are CPT analogs, creating negative-positive radiation pressure ( https://en.wikipedia.org/wiki/Radiation_pressure#Radiation_pressure_from_momentum_of_an_electromagnetic_wave ), we can imagine (unidirectional) ring laser as a pump. Below is such hydrodynamical analog - in pump with fluid running in circles, flow to split down is reduced by negative radiation pressure. The question to test is if it also true for ring laser: if intensity from beam splitter down is changed by opening/closing the shutter? If so, a bit more complex setting would lead to two-way quantum computers.

Optical pulling allows to pull in optical tweezers, negative radiation pressure to pull solitons - some hypothetical application: 2WQC (two-way quantum computers) maybe solving NP problems (standard 1WQC might be bounded with e.g. Shor, Grover). I would gladly discuss and generally am searching for collaboration in these topics, especially access to ring laser to test if it allows for negative photon pressure, what is required e.g. by CPT symmetry.

In CPT perspective the absorption equation would act on CPT(target on the left), what means emission equation acts on it in standard perspective (no CPT). This equation work only if there are excited atoms: N_2 > 0, hence we can use e.g. a lamp here continuously excited in corresponding spectrum - usually deexciting in isotropic way, opening the shutter additionally with the emission equation - increased probability of deexciting toward the laser, what would be seen as reduced intensity by detectors around.

Looking at the diagram, absorption equation applies to the central and right targets (shifted behind right mirror), the emission equation to the central - the question is if also to the left (shifted behind left mirror). From CPT perspective the equations would switch, the absorption equation would apply to CPT(central target) and to CPT(target on the left) - the latter means without CPT the emission equation would apply to the target on the left. While <E x H>/c radiation pressure can be negative (e.g. https://scholar.google.pl/scholar?q=negative+radiation+pressure ), turns out there are lots of optical pulling experiments, beside optical tweezers awarded with 2018 Nobel Prize, here is good summary: https://opg.optica.org/oe/fulltext.cfm?uri=oe-31-2-2665&id=525052 Seems all of them is pulling of objects with light, while ring laser should have related by different - pulling of photons, negative photon pressure, external stimulated emission.

Exactly, excited target usually deexcite in isotropic way, due to laser should additionally accordingly to the stimulated emission equation on the left - negative radiation pressure should increase probability of deexcitation in this direction, reducing monitored intensity seen by detectors around this target.

By "CPT(target on the left)" I have meant with applied all 3 symmetries. Or let us look from perspective of of radiation pressure : <E x H>/c, if ring laser creates positive radiation pressure, from perspective after CPT doesn't it mean negative?

From perspective after CPT symmetry the photons would travel toward CPT(target on the left) - if physics works the same after this symmetry, toward "minus time" this target would be excited accordingly to equation on the right, what toward "plus time" means it would be deexcited accordingly to the equation on the left ... if only it was excited in the first place like lamp: N_2 > 0. As ring laser causes "positive radiation pressure" in one direction, from perspective after CPT it means causing "negative radiation pressure".

Also, pulling with photons is done e.g. by https://en.wikipedia.org/wiki/Optical_tweezers EM radiation pressure is <E x H>/c ( https://en.wikipedia.org/wiki/Radiation_pressure#Radiation_pressure_from_momentum_of_an_electromagnetic_wave ) - doesn't have to be positive.

Turns out there is considered "negative radiation pressure" - predicted for solitons, searched e.g. for mechanical waves on graphene: https://scholar.google.pl/scholar?q=negative+radiation+pressure ... so the question is if it could be realized with EM waves, photons using lasers? Because believing in CPT symmetry, from its perspective photon trajectories would be reversed, the target on the left would be "standard target" to which we "push photons" (absorption equation), what from perspective without CPT would mean emission equation, "pulling photons", "negative radiation pressure".

The T transform here reverses photon direction, making the laser cause excitation of target on the left, what means causing deexcitation without T symmetry. Look at the two equations (from https://en.wikipedia.org/wiki/Stimulated_emission#Mathematical_model ) - to which of 3 targets they apply? The equation on the right applies to the central and right target. The equation on the left applies to the central target - my point is it also symmetrically applies to the target on the left - because in perspective after CPT symmetry the equations are switched.