Everything posted by Duda Jarek
-
What is the size and shape of single optical photon?
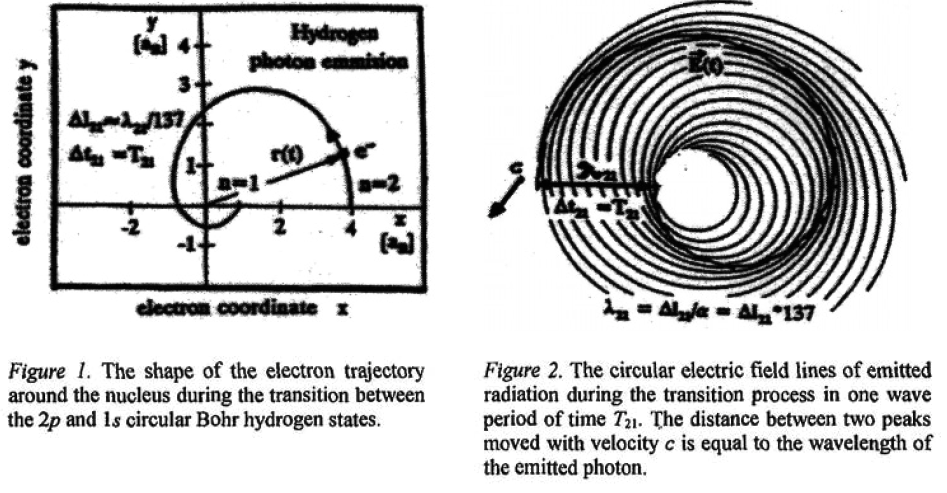
EM field as consequence of electron dynamics travels with speed of light: ~0.3 nm per attosecond. Here is some paper trying to model emission of photon from hydrogen: https://link.springer.com/chapter/10.1007/0-306-48052-2_20
-
What is the size and shape of single optical photon?
Sure such photon dynamics is extremely complex, but it doesn't mean we should just neglect this fundamental problem of understanding physics. For example while naively quantum processes are instant, reaching such measurement possibility, turns out e.g. that photoemission takes a few dozens of attoseconds: https://science.sciencemag.org/content/328/5986/1658 - there is some concrete hidden electron dynamics leading to EM field wave of the photon, we should at least try to understand. The ellipsoid view is probably only an approximation of energy density shape, to understand e.g. Mach-Zehnder there should be also some pilot/theta wave flying the second path, like from http://redshift.vif.com/JournalFiles/V16NO2PDF/V16N2CRO.pdf :
-
What is the size and shape of single optical photon?
I have just found another - 2021 with more sophisticated models: "The size and shape of single photon" http://dx.doi.org/10.4236/oalib.1107179 Sure, these might be just the beginnings ... but asking for EM field configuration of photons is valid question, also from quantum perspective: as Feynman ensemble of classical ones - we can ask for e.g. dimensions averaged over such ensemble.
-
What is the size and shape of single optical photon?
The basic difference between classical mechanics and quantum, is that in the former we have single trajectory optimizing action, while in the latter we have Feynman ensemble of trajectories, fields etc. So the question can be seen: what is mean size of such photon's energy density - averaged over quantum ensemble. QM cannot be used to completely neglect such a basic question of physics, and we have also experimental arguments like quoted above.
-
What is the size and shape of single optical photon?
"Detecting" by who, what? This is very subjective question, while I am asking for objective EM field configuration - telling anything concrete about it. While this is a difficult question, there are at least these two articles, most importantly - providing experimental arguments (quoted in post above). What do you think about them?
-
What is the size and shape of single optical photon?
Photon is EM field, the basic question is energy density distribution of EM field for single photon - some rho ~ |E|^2 + |B|^2 ( https://en.wikipedia.org/wiki/Electric_field#Energy_in_the_electric_field ). Can we say anything concrete about this energy distribution, preferably based on experimental arguments like mentioned above? Ps. Paper by different author: https://arxiv.org/pdf/1604.03869
-
What is the size and shape of single optical photon?
Optical photon is produced e.g. during deexcitation of atom, carrying energy, momentum and angular momentum difference. So how is this energy distributed in space - what is the shape and size of single photon? Looking for literature, I have found started by Geoffrey Hunter, here is one of articles: "Einstein’s Photon Concept Quantified by the Bohr Model of the Photon" https://arxiv.org/pdf/quant-ph/0506231.pdf Most importantly, he claims that such single optical photon has shape similar to elongated ellipsoid of length being wavelength λ, and diameter λ/π (?), providing reasonably looking arguments: Is it the proper answer? Are there other reasonable answers, experimental arguments?
-
1D transverse-field Ising model - what is the difference between its classical and quantum treatment?
The 1D transverse field Ising model is usually solved in quantum way, but we can also solve it classically - parametrize angles of spins and use Boltzmann ensemble of sequences of spin angles: Pr(σ)∝exp(−H(σ)) for σ=((cos(αi),sin(αi)))i∈Z getting Markov process of angles, which can be easily approximated with Maximal Entropy Random Walk, for example getting below joint distributions for (αi, αi+1) for various parameters (Section III here ) : As intuition suggests, there is some thermal wobbling of spin directions: (anti)aligned for dominating J, in x axis for dominating h. However, in quantum approaches there are only considered spins in four directions, so should we imagine that intermediate angles are obtained by superposition? Should there be thermal wobbling of spin directions as in densities above? What are the differences in interpretation and predictions between such looking natural classical treatment and the quantum one?
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
Ok, I have finally looked closer (paper: https://link.springer.com/article/10.1140%2Fepjc%2Fs10052-018-5918-6 ). So basically they believe that B mesons should decay symmetrically to electrons and muons, but they observe slight asymmetry: ~15% more to electrons with 3.1 sigma (~1/1000). Mesons is huge family: https://en.wikipedia.org/wiki/List_of_mesons Beside kaons (~500Mev), we mainly know pions: charged have ~140Mev, ~10^-8s lifetime, mainly decay to muon + neutrino ... but also have rare decay to electron + neutrino ( https://en.wikipedia.org/wiki/Pion#Charged_pion_decays ). B mesons ( https://en.wikipedia.org/wiki/B_meson ) have ~5GeVs ... while pions have very asymmetric decay into leptons, I have to admit that I don't understand why slight asymmetry for other mesons is surprising (?) Anyway, in discussed "biaxial nematic perspective", mesons nicely fit fluxons forming loop with additional internal twist (corresponding to strangeness), maybe hopfion (diagram below from https://en.wikipedia.org/wiki/Hopf_fibration ). The three types/quarks are from performing such loop along one of 3 axes of biaxial nematic. Mesons are configurations being local energy minima - their asymmetry of decay into various leptons is completely unsurprising.
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
studiot, thanks, probably as usual it is matter of adding/modifying terms to Lagrangian - in practice used in perturbative approximation, literally adding terms to Taylor expansion. But this is description not understanding, neglecting basic questions like of field configuration behind given Feynman diagram, mean energy of fields in given distance from electron etc. Or renormalization literally subtracts infinite energy by hand - where exactly it subtracts it? Shouldn't it in fact subtract some energy density - from e.g. energy density of electric field, to make it integrate to finite energy. Search for deeper models - effectively described by something close to Standard Model, is just no longer ignoring such basic questions. Like of regularized EM field around electron - including renormalization procedure, this way integrating to finite energy. Or explaining basic properties of physics - instead of inserting them by hand, e.g.: - Why electric charge is quantizatized? In liquid crystal experiments: because it is topological charge. - Why we have 3 leptons? In biaxal nematic view: because we have 3 spatial directions. - Why leptons also need magnetic dipole. ... because of hairy ball theorem. - Why proton is lighter than neutron? ... because baryons require charge, which in neutron needs to be compensated. - How nuclei overcome Coulomb repulsion? ... by being bind with fluxons.
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
There are more long-range interactions for liquid crystals, e.g.: dipole-dipole: "Novel Colloidal Interactions in Anisotropic Fluids" https://science.sciencemag.org/content/275/5307/1770 Coulomb (!): "Coulomb-like interaction in nematic emulsions induced by external torques exerted on the colloids" https://journals.aps.org/pre/abstract/10.1103/PhysRevE.76.011707 Skyrme models are for strong interaction ... so why can't we model all? These liquid crystal systems are for uniaxial nematic - one distinguished axis everywhere ... bringing a question about natural generalization: biaxial nematic: 3 distinguished axes in 3D (4 in spacetime adds gravity) - giving particle-like configurations resembling 3 leptons, neutrinos, baryons, nuclei ...
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
Another long-range interaction in liquid crystal paper: "Long-range forces and aggregation of colloid particles in a nematic liquid crystal": https://journals.aps.org/pre/abstract/10.1103/PhysRevE.55.2958 This time V ~ 1/d^5, highly anisotropic ... like quadrupole-quadrupole interaction.
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
I can respond tomorrow, but in sine-Gordon the field can be interpreted as of phases of these penulums in lattice - with minimum of gravitational potential every 2pi. For Couder and other hydrodynamical QM analogues (Casimir, Aharonov-Bohm etc.), here are gathered materials: https://www.dropbox.com/s/kxvvhj0cnl1iqxr/Couder.pdf
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
Energy density, Hamiltonian is a first step - convenient to start with as all the terms have positive conteibutions. It is often timespace symmetric - not distinguish time and space directions. But for solving such model we indeed usually go through the Legendre transform to Lagrangian - both for the least action formulation, and the Euler-Lagrange equation. I have tried to go this way for the biaxial nematic with Coulomb interaction, but it was too tough for me. Hamiltonian alone can be used to find static solutions, like this kink in sine-Gordon as minimal energy transition between two vacua. However, electron should be finally a dynamical solution - with this zitterbewegung, de Broglie clock ~10^21 Hz oscillations, confirmed experimentally: https://link.springer.com/article/10.1007/s10701-008-9225-1q
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
Let me bring back my two responses, both are crucial for the model: The number of found particles is in hundreds/thousands now. Some are virtual, like 80GeV boson W in beta decay of 1GeV neutron - this mass should be rather imagined as only shape of energy dependence like for https://en.wikipedia.org/wiki/Effective_mass_(solid-state_physics) What we should target (as configurations being local energy minima) are especially more stable particles and their decay modes e.g. from https://en.wikipedia.org/wiki/List_of_baryons ... and a general behavior in this table is decay with pion or kaon to baryon with lower strangeness. As discussed, there are many reasons to imagine baryons in this biaxial nematic perspective as loop of one vortex around another vortex. We have three types of vortices, allowing for quark-like interpretations. Possible complication of such simplest knot is additional internal twist of its vortex loop around - it should be obtainable in high energy collisions, and should relax by releasing part of this twist as particle - pion, kaon (bottom of diagram below) ... getting nice agreement if interpreting the number of internal twists as strangeness. There are considered strageness 4 baryons (e.g. https://arxiv.org/abs/2011.05510 ). The space of local minima of configuration space can be quite complex: 3 types of vortices, they can contain charge (e.g. hedgehog), additional twist for loop around - can lead to hundreds of metastable states for baryons. In these models we have energy density (Hamiltonian, can be translated to Lagrangian) - usually with some spatial derivatives like stress, temporal for kinetic behavior, and potential (e.g. Higgs-like) ... integrating energy density we get mass of particle, usually scaling as in SR thanks to Lorentz invariance. Unfortunately it is quite tough calculation, I have attached for kink of sine-Gordon a few posts ago. We can parametrize with positions of ansatz configurations like hedgehog, Lorentz transformed for velocities, getting classical mechanics approximations ... with kinetic energy going into mass exactly as in special relativity. Fluxons are quite complex. While they are usually studied in superconductors/superfluids, here they are also needed in vacuum, e.g. to bind nucleus against Coulomb repulsion. Probably the best experimental argument are "magnetic flux tubes" - nearly 1D shining structures seen in Sun's corona, they carry energy density per length - which can be released while shortening in https://en.wikipedia.org/wiki/Magnetic_reconnection Quote from "Physics of Magnetic Flux Tubes" by Ryutova: "Vortices in superfluid Helium and superconductors, magnetic flux tubes in solar atmosphere and space, filamentation process in biology and chemistry have probably a common ground, which is to be yet established. One conclusion can be made for sure: formation of filamentary structures in nature is energetically favorable and fundamental process. "
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
studiot, I had long fluxon response, response about baryons and strangeness - both disappeared. This sine-Gordon kink represents solution minimizing energy e.g. in lattice of pendulums: of phases while twisting by pi. But this is the most basic model - you can find it in hundreds of books and papers - please start with looking closer at external sources.
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
Please formulate a question and I will try to answer. Sure the basic one is why I haven't moved it forward with simulations ... because the details are tougher than it sounds. To make Gauss law count winding number/topological charge as in Faber's approach, we need to define EM field as curvature of such SO(3) biaxial nematic field, then use EM energy density: as sum of squares of these curvatures. Below is such approach, using representation as 3x3 real symmetric tensor, with Higgs-like potential: preferring some set of 3 eigenvalues - shape of nematic in SO(3) vacuum. One difficulty is translating such energy density from rotation matrix O to the actual tensor M (quite subtle). Second is getting Euler-Lagrange equation (I wasn't able to get), or work on ansatz avoiding them. Third is choosing details of this Higgs-like potential, in fact containing weak and strong interactions. It was too tough for me and I gave up, hoping to find help.
-
hijack from Similarity between particle physics and macroscopic quantum phenomena like fluxons?
Maxwell equations have this weakness of allowing for any real electric charge, while nature has charge quantization at heart - only integer charges are allowed (at least asymptotically: far from particles). We can repair this disagreement e.g. by making Gauss law count winding number/topological charge (Faber) - which has to be integer ... then its simplest nontrivial charge becomes a model of electron - the question is how to expand it to get all the particles?
-
hijack from Similarity between particle physics and macroscopic quantum phenomena like fluxons?
The number of found particles is in hundreds/thousands now. Some are virtual, like 80GeV boson W in beta decay of 1GeV neutron - this mass should be rather imagined as only shape of energy dependence like for https://en.wikipedia.org/wiki/Effective_mass_(solid-state_physics) What we should target (as configurations being local energy minima) are especially more stable particles and their decay modes e.g. from https://en.wikipedia.org/wiki/List_of_baryons ... and a general behavior in this table is decay with pion or kaon to baryon with lower strangeness. As discussed, there are many reasons to imagine baryons in this biaxial nematic perspective as loop of one vortex around another vortex. We have three types of vortices, allowing for quark-like interpretations. Possible complication of such simplest knot is additional internal twist of its vortex loop around - it should be obtainable in high energy collisions, and should relax by releasing part of this twist as particle - pion, kaon (bottom of diagram below) ... getting nice agreement if interpreting the number of internal twists as strangeness. There are considered strageness 4 baryons (e.g. https://arxiv.org/abs/2011.05510 ). The space of local minima of configuration space can be quite complex: 3 types of vortices, they can contain charge (e.g. hedgehog), additional twist for loop around - can lead to hundreds of metastable states for baryons.
-
hijack from Similarity between particle physics and macroscopic quantum phenomena like fluxons?
In these models we have energy density (Hamiltonian, can be translated to Lagrangian) - usually with some spatial derivatives like stress, temporal for kinetic behavior, and potential (e.g. Higgs-like) ... integrating energy density we get mass of particle, usually scaling as in SR thanks to Lorentz invariance. Unfortunately it is quite tough calculation, I have attached for kink of sine-Gordon a few posts ago. We can parametrize with positions of ansatz configurations like hedgehog, Lorentz transformed for velocities, getting classical mechanics approximations ... with kinetic energy going into mass exactly as in special relativity. Fluxons are quite complex. While they are usually studied in superconductors/superfluids, here they are also needed in vacuum, e.g. to bind nucleus against Coulomb repulsion. Probably the best experimental argument are "magnetic flux tubes" - nearly 1D shining structures seen in Sun's corona, they carry energy density per length - which can be released while shortening in https://en.wikipedia.org/wiki/Magnetic_reconnection Quote from "Physics of Magnetic Flux Tubes" by Ryutova: "Vortices in superfluid Helium and superconductors, magnetic flux tubes in solar atmosphere and space, filamentation process in biology and chemistry have probably a common ground, which is to be yet established. One conclusion can be made for sure: formation of filamentary structures in nature is energetically favorable and fundamental process. "
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
I again recommend sine-Gordon model to understand massive particles - containing rest energy which can be released in annihilation, also working as inertial mass due to Lorentz invariance ... and such particles can only approach the propagation speed c, at cost of energy growing to infinity, it cannot exceed this velocity. It is safer to directly target experimental properties like charge distribution - which is also suggested in this"biaxial nematic field" ... then interpret fractional charges as quarks, interaction between them as gluons and pions. Another big hint is deuteron - we know it has large electric qadrupole moment ( https://en.wikipedia.org/wiki/Deuterium#Magnetic_and_electric_multipoles ) - hard to imagine for just proton+neutron, but suggested in the discussed model: neutron needs charge, so proton shares part of its charge - leading to savings as binding energy, and observed quadrupole moment. Topological charge is the winding number for function f:S->S from e.g. sphere around some point, into e.g. sphere of vectors Winding number of this f:S->S functions can be obtained by integrating over Jacobian, which is curvature of this vector field - getting Gauss law as Gauss-Bonnet theorem, with built in charge quantization as topological:
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
If you look at the big framework diagram above, for many reasons baryons resemble simplest knots: one vortex around another, proton/neutron should be such lowest energy pairs ... then they can form various size knots: nuclei (binded against Coulomb), including halo neutrons ( https://en.wikipedia.org/wiki/Halo_nucleus ) stably binded in distance a few times larger than standard nuclear force. The external vortex loop enforces partial hedgehog-like configuration in the center vortex - proton can just enclose it to entire hedgehog, what means +1 topological charge - corresponding to elementary e electric. But neutron has to compensate this partial hedgehog/charge to zero, what requires increased size and so larger energy/mass ... while asymptotically we have charge quantization (as topological), locally there can be such partial configuration/charge like quarks, but it comes with additional energy. Here are a few sources also claiming such charge distribution for neutron: positive core, negative shell: https://inspirehep.net/literature/1377841 , http://www.actaphys.uj.edu.pl/fulltext?series=Reg&vol=30&page=119 , http://www.phys.utk.edu/neutron-summer-school/lectures/greene.pdf :
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
@joigus, these are matters of interpretation, e.g. in perturbative QED interpretation Coulomb interaction is performed with photon exchange ... Should we really imagine some infinite sequence of exchanged photons e.g. between proton and electron in hydrogen atom? Or maybe should we remind that it is perturbtaive approximation - like expanding into Taylor series and representing terms of this series - where Feynman diagrams mathematically came from. In liquid crystal we get Coulomb-like long range interaction because the further e.g. opposite topological charges are, the larger total energy (stress) of the entire field is, e.g. with V(r) ~ 1/r behavior for Coulomb: In perturbative approximation you could get Taylor series and imagine it as photon exchanges, but this is just a different interpretation. So it is safer not to focus on interpretations first, but directly on particle behaviors like Coulomb interaction, decay modes - on agreement there first, then search for correspondence with perturbative QFT approximation of the Standard Model. What particle behavior you think is wrong in the framework I have presented? It also e.g. gets fractional charges in neutron ("quarks") - explaining why it is heavier than proton. Its topologically nontrivial vacuum requires Higgs-like potential corresponding to mass of particles - it allows to deform electromagnetism into other interactions in the center of particles - to avoid the infinite energy of electric charge issue.
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
I don't understand what do you mean by abstract space? E.g. sine-Gordon has mechanical realization as in the video, interaction between topological solitons is realized e.g. between fluxons in superconductors, long-range interaction is realized in liquid crystals (e.g. https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract ). This is about finding field and Lagrangian to get similarity with particles and fields - also the very real EM field. About repairing this very real EM field: that Gauss law in nature only returns integer charges ... what is done here by interpreting charge as topological, with Gauss-Bonnet theorem as Gauss law ... then the simplest nontrivial charge becomes a simple model of electron. This "biaxial nematic field" can be realized with a real symmetric tensor, exactly as stress-energy tensor in general relativity, by just using Higgs-like potential for it: preferring topologically nontrivial vacuum e.g. S^2, SO(3). But it is safer to be agnostic about its realization for this moment - first get the particles rights, then try to interpret the field e.g. with GR stress-energy tensor or some superfluid vacuum.
-
Similarity between particle physics and macroscopic quantum phenomena like fluxons?
Sine-Gordon: just phi_tt = phi_xx - sin(phi) has already massive particles with quantized topological number, pair creation/annihilation, and entire special relativity: Lorentz contraction, time dilation, SR mass/momentum scaling ... studying this looking trivial toymodel is the best way I know to really feel the special relativity. Going to higher dimensions, here is example of observing long-range F~1/D force for topological solitons in liquid crystal: https://pubs.rsc.org/en/content/articlelanding/2019/sm/c9sm01710k#!divAbstract We can choose dedicated Lagrangian to get exactly Coulomb interaction for them with included charge quantization as topological - e.g. Faber's way ( https://iopscience.iop.org/article/10.1088/1742-6596/361/1/012022/pdf ) : define EM field as curvature of some deeper vector field, this way Gauss law counts winding number - topological charge. But the goal is getting all the particles/interactions with dedicated field and Lagrangian - I have a framework, a sketch of Lagrangian, but getting the details + simulations was too difficult for me. Here is the sketch of this general framework again I would gladly discuss - for superfluid biaxial nematic field - of 3 distinguished axes: 1) we get 3 hedgehog realizations of one of 3 axes - kind of 3 leptons (the same charge, different energy/mass), with magnetic dipole due to the hairy ball theorem, Faber's approach gives Coulomb interaction for them, 2) the simplest vortex loop resembles neutrino: stable - very difficult to interact with, 3 types: along one of 3 axes, can "oscillate" between them by internal rotation, are produced in beta decay, 3) loop with internal twist (hopfions?) might correspond to mesons, number of twists nicely fits strangeness - agrees with decay of mesons, strange baryons ( https://en.wikipedia.org/wiki/List_of_baryons ), 4) if another vortex goes through such loop, it nicely resembles baryons, interaction between its vortices creates charge inside (diagram below). Proton just closes this charge, while neutron has to compensate it - what is costly, explaining why neutron is heavier than proton (also quark-like fractional charge distribution), 5) combining baryons form nuclei as various size knots - binding them against Coulomb repulsion, including halo neutrons binded in much larger distance ( https://en.wikipedia.org/wiki/Halo_nucleus )