Duda Jarek

But excited atoms radiate abundant energy - getting to the lowest energy: ground state? So why shouldn't unaligned spin radiate abundant kinetic energy - getting to the lowest energy: aligned spin? ... especially that this is exactly what they observe in Stern-Gerlach ... and EM says that oscillating dipoles should radiate energy. Indeed, and in Stern-Gerlach we have free unbounded objects - having magnetic dipole, in external magnetic field - as also e.g. electrons in synchrotron radiating energy as EM waves. Magnetic dipole in external magnetic field gets torque - Larmor precession ... rotating dipole creates varying EM fields - like antenna radiating energy as EM waves, of power given by the used formula. Larmor precession comes from torque - works in all scales: from electron to macroscopic magnets. For non-polarized beam, the original direction of magnetic dipole is random, the final in Stern-Gerlach is aligned in parallel or anti-parallel way - exactly as we would expect for a classical magnet in external magnetic field.

There is this formula for power of rotating electric dipole: http://www.phys.boun.edu.tr/~sevgena/p202/docs/Electric dipole radiation.pdf Inserting k = 10^6 Hz and p ~ 10^-23, you get power ~10^-4 W ... proper calculations would require someone experienced with antennas, but generally we are talking about ~femtosecond scales. We are talking about rotating dipole and acceleration of charges/dipoles generally leads to radiation of energy as EM waves, e.g. in bremsstrahlung. The above formula is for oscillating dipole, getting the details is difficult I will think about, but generally these are ~femtosecond scales. ... and this radiation says that magnetic dipoles should align in magnetic filed - what is exactly what they observe e.g. in Stern-Gerlach.

Imagine you have some object e.g. atom, and put it into precessing coordinates - it would introduce additional time derivative terms (kinetic), until stopping this precession.

I have described classical radiation explanation leading to the same conclusion as Stern-Gerlach: of finally aligned spins. I have used the formula for EM radiation energy of antenna as oscillating dipole in the first post here. This is a complicated problem - it would be great if somebody experienced in antennas could make a better calculation. If it would be a macroscopic magnet, torque should lead to precession. Exactly the same argument is used for electron in https://en.wikipedia.org/wiki/Larmor_precession So why there shouldn't be precession in intermediate scale: of atom? And precession means additional kinetic energy - contributions with time derivative, which can be minimalized by just aligning spin - what they experimentally observe e.g. in Stern-Gerlach.

Such need is suggested by conservation laws - especially of energy and angular momentum. Magnetic dipole of random direction in external magnetic field has abundant energy (kinetic of precession) - in Stern-Gerlach somehow lost by aligning, so what happens with this energy difference? Could turn into heat, through EM interactions. Also angular momentum is different for a random initial spin and aligned final spin - what has happened with this difference? There are two effects here - "V cdot mu" energy as in Zeeman effect, and kinetic energy from precession of unaligned spin. In Stern-Gerlach the latter seems to dominate, but there should be also statistical difference of population of two beams (?) - although, it might be extremely tiny. The problem is that classical theory of radiation predicts exactly the same outcome - magnetic dipole in external magnetic field gets torque, additional kinetic energy of precession - as oscillating dipole should should EM radiate energy, until reaching minimum: when it is aligned ... exactly as seen in Stern-Gerlach. So what is the difference between such classical behavior of magnet in magnetic field, and what they observe in Stern-Gerlach?

Textbook explanation of this kind of quantum effects is usually "unitary evolution ... magic happens ... unitary evolution" ... I would gladly see a better one, getting inside this magic, and experimentally it slowly becomes accessible - e.g. they measured ~20 attosecond delay of photoemission: https://www.science.org/doi/10.1126/science.1189401 ... what is happening during such 20as? If atom has magnetic dipole moment e.g. due to angular momentum, then in external magnetic field it gets torque, hence its axis should precess - what means additional kinetic energy. There is tendency to release abundant energy, and mechanism for oscillating dipole - due to acceleration of charge/dipole, as e.g. for electron in bremsstrahlung. However, there appears question, issue of quantization of such released EM energy - I completely agree it can directly manifest as heat ... but what if they are single atoms in vacuum? The belief that everything EM related is through quantized photons probably comes from pertubative approximation of QFT e.g. seeing Coulomb interaction through photon exchange ... but this is our approximation - fundamental question should be for non-perturbative. A common alternative is quantization through emitter/absorber - usually being atoms of quantized energy states. E.g. cosmic microwave background radiation seems just a thermal noise of EM degrees of freedom - quantized when absorbing its energy by atoms. The problem starts with antennas e.g. linear - producing cylindrically-symmetric EM waves. Assuming such wave consists of a finite number of photons, going with distance to infinity such discrete photons would become infinitely diluted, large ...

Conservation laws e.g. Noether theorem say that change of energy, momentum, angular momentum - has to be compensated with opposite change e.g. in EM field, for example: excited atom <-> deexcited atom + EM wave carrying difference of energy, momentum and angular momentum From the other side, accelerating charges/dipoles leads to radiation of some energy as EM waves ... and e.g. spin echo in pulsed EPR shows everything works down to electron scale. I think you agree that classical magnet in magnetic field should EM radiate energy and finally align (to zero torque μ×B=0) ... they also see it for atoms in Stern-Gerlach ... if you claim these are different mechanisms, please elaborate on the mechanism seen in Stern-Gerlach? Cannot we see it as unaligned "random" spin <-> aligned spin + EM wave carrying difference of energy, momentum and angular momentum?

So how do you understand/explain Stern-Gerlach experiment: why these atoms align in parallel or anti-parallel way (as "classical magnets" would through radiation of abundant kinetic energy)? What happens with the difference of energy and angular momentum (between initial random and final aligned spins) if it is not radiated as EM wave?

Precession is not just "a classical concept" - it applies also to electron, even for much more complex acrobatics in spin echo: https://en.wikipedia.org/wiki/Electron_paramagnetic_resonance#Pulsed_electron_paramagnetic_resonance I think you agree that macroscopic magnet in external magnetic field would get torque, precession ... undergo "classical EM radiation" down to minimal energy μ×B=0 ... as also observed in Sterin-Gerlach. So how small could such magnet be? What happens when this magnet becomes extremely tiny: of size of atom ... electron?

For atom the dominating magnetic dipole moment can come e.g. from angular orbital momentum - in which case shouldn't Larmor precession be of angular momentum direction? For any (also macroscopic) magnet in external magnetic field there is τ=μ×B torque leading to precession, what means oscillating dipole - type of antenna, radiating energy with power as the above formula ... until reaching the lowest energy state: μ×B=0 having minimal kinetic terms.

Stern-Gerlach experiment is often seen as idealization of measurement. Using strong magnetic field, it makes magnetic dipoles (of e.g. atoms) align in parallel or anti-parallel way. Additionally, gradient of magnetic field bends trajectories depending on this choice. Magnetic dipoles in magnetic field undergo e.g. Larmor precession due to τ=μ×B torque, unless μ×B=0 what means parallel or anti-parallel alignment. Precession means magnetic dipole becomes kind of antenna, should radiate this additional kinetic energy. Thanks to duality between electric and magnetic field, we can use formula for precessing electric dipole, e.g. from this article: Using which I get power like 10^−3 W, suggesting radiation of atomic scale energies (∼10^−18 J) in e.g. femtoseconds (to μ×B=0 parallel or anti-parallel). So can we see spin alignment in Stern-Gerlach as a result of EM radiation of precessing magnetic dipole? Beside photons, can we interpret other spin measurement experiments this way?

Just prepared: https://arxiv.org/pdf/2112.12557 While textbook explanation of p-n junction ( https://en.wikipedia.org/wiki/P–n_junction ) looks quite heuristic, this is just using statistical mechanics - no "holes", only electron dynamics. Lattice 60x30 atoms below, dopants of different potentials are presented as red/green dots, grayness shows calculated electron densities, arrows show local currents. The model is: - use 3 types of potentials: of individual atoms + from external voltage + mean-field self interaction (from found charge density), - apply entropy maximizing diffusion ( https://en.wikipedia.org/wiki/Maximal_entropy_random_walk ), getting e.g. below diagrams. Are there there others atomic-scale conductance models? What applications could they have, e.g. some technology optimization? ps. simpler simulator: https://demonstrations.wolfram.com/ElectronConductanceModelsUsingMaximalEntropyRandomWalks/ reddit discussion: https://www.reddit.com/r/electronics/comments/rmxjd4/inexpensive_atomicscale_conductance_model/

Some updates - interactive demonstration to play with such topological charges of liquid crystal biaxial nematic - of 3 types resembling 3 leptons, requiring magnetic dipoles, with analogy of quantum phase evolution: https://demonstrations.wolfram.com/TopologicalChargesInBiaxialNematicLiquidCrystal/ Derivation of Klein-Gordon-like equation for this evolving phase (slide 15 of https://www.dropbox.com/s/9dl2g9lypzqu5hp/liquid crystal particles.pdf )

Paper: https://arxiv.org/pdf/2108.07896 Slides: https://www.dropbox.com/s/9dl2g9lypzqu5hp/liquid crystal particles.pdf Hypothesized further particles, e.g. proton lighter than neutron - because baryons structurally require charge here, neutron has to compensate it what costs energy ... in deuteron two baryons hare single charge - getting electric quadrupole moment and aligned spins as in physics:

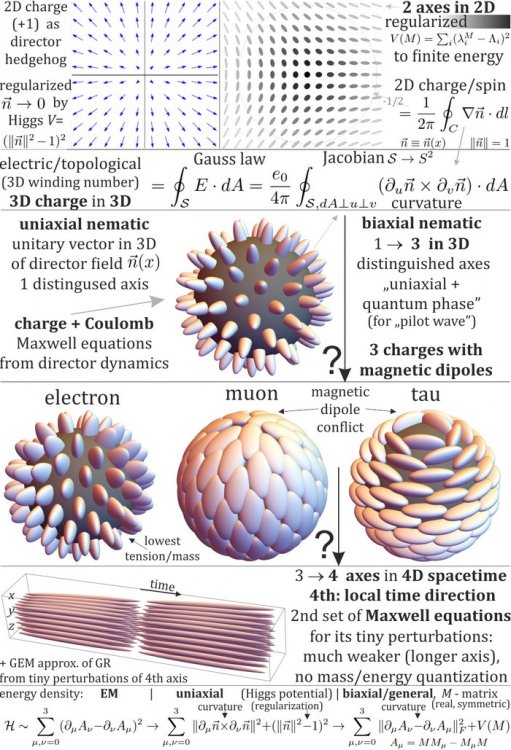
I have finally worked out mathematical framework up to Euler-Lagrange for this ellipsoid field/liquid crystal like approach: - field of 3 distinguishable axes using 3x3 matrices preferring fixed set of eigenvalues, - hedgehog of one of 3 axes for 3 leptons - charges governed by Maxwell equations, with magnetic dipole moment due to hairy ball theorem, - then expanding to 4x4 matrices we get second set of Maxwell equations for GEM ( https://en.wikipedia.org/wiki/Gravitoelectromagnetism ). The approach generalizes Faber's from vector to matrix field. Electromagnetic (A vector, F tensor) are no longer just (connection Gamma, curvature R), but additionally include dependence of rotated shape (eigenvalues). This way we can get vacuum dynamics of 3 strengths: EM >> pilot wave >> GEM. Below is the main diagram with concepts. I have submitted to arxiv but is "on hold" as usual, so I have put it here: https://www.researchgate.net/publication/353932148_Framework_for_liquid_crystal_based_particle_models It is initial version I will work on especially: - the details of potential to choose is the main open question, and very difficult one - it contains weak/strong interactions, - explaining gravitational mass - spatial curvature caused e.g. by energy density, activation of potential, - finally numerics first aiming agreement with electron, 3 leptons, hopefully enforcing intrinsic periodic process: de Broglie clock. Would gladly discuss/collaborate.

Sure, Iran managed to ban, but if the exponential trend continues, they grow in money, power, influence - making defense more and more difficult. I have no idea on what percentage of world energy consuption cryptocurrencies could finally stabilize at?

Sure, as you mention, these ways have various costs based on physical limitations - market should stabilize on the cheapest ways up to profitability level, which grows with gold price. The problem is that potentially infinite number of various cryptocurrencies do not have such physical limitations - hence can grow to consume just all available resources ... ... unless being banned like https://www.cnbc.com/2021/05/26/iran-bans-bitcoin-mining-as-its-cities-suffer-blackouts.html

Sure electricity cost is lower, but total cost (including e.g. hardware) market is willing to pay for $100 banknote is ~$99 ... giving the miner/investor $1 profit, at $99 cost for civilization ... plus e.g. these $37-49 "in health and climate damage" externalities. Sure mining of gold/silver also has externalities - which should be included in evaluation of such investement, compensated e.g. through taxes to those who pay them ... but 1) In contrast to massive hashing, our civilization needs these metals e.g. to make electronics: https://en.wikipedia.org/wiki/Gold#Electronics https://en.wikipedia.org/wiki/Silver#Electronics 2) in contrast to potentially infinite number of various cryptocurrencies which can consume all available resources, real mining has reasonable physical limits for used resources.

As suggested, I have searched for "BTC cost of mining", getting https://www.bloomberg.com/opinion/articles/2021-05-25/bitcoin-s-btc-cost-to-society-is-impossible-to-ignore These are additional externalities, one type of many completely ignored by miners. Your estimation seems to correspond to energy cost only, but even miners themselves have more costs - especially hardware (which will not satisfy other utility, which manufacturer did not produced other electronics), also e.g. human costs and many others. The rules of market say that total amortized costs paid by investors/miners should stabilize at paying ~$99 worth various resources for $100 banknote ... and looking at bitcoin price and its energy consumption in one plot, they have nearly identical trends: annual energy consumption in TWh is ~price / $100.

Sure, maintaining Bitcoin's last 6 year 2x growth/year for the next 6 years is hopefully impossible (but looks like many speculators believe it will happen). But there are thousands of cryptocurrencies, also "evolving" to consume succeeding resources (e.g. https://www.theguardian.com/technology/2021/may/26/new-cryptocurrency-chia-blamed-for-hard-drive-shortages ) ... So what percentage of world resources could be stable attractor for crypto consumption - somehow balancing observed pursue for individual gains? Balancing with what?

The general issue is that we don't have "mind of a civilization wanting the best for it" ... but rather individuals pursuing individual gains. E.g. if getting opportunity to get $100 banknote by burning $99 worth resources (e.g. through calculating hashes), we can see individuals massively do it - for $1 individual profit, no matter it means $99 resource loss for civilization.

Many countries have low fertility problem of decreasing (TFR<2.1) and aging population ... beside developing countries - which will reduce fertility when most children start surviving to become an adult, also with education. Sure food production might become a huge problem due to climate change ... another huge problem is drinking water e.g. https://www.unicef.org/stories/water-and-climate-change-10-things-you-should-know ps. https://en.wikipedia.org/wiki/Total_fertility_rate : https://www.nature.com/articles/nature08230 :

Population growth seems prevented by just children survivability, improved live quality - see e.g. some Hans Rosling talks like Exponentially growing additional waste makes fight with climate change even more hopeless ... 1 individual can easily exceed a million times required consumption here - it doesn't matter that 99% of population care and save resources, if 0.001-th percentile can saturate close to 100% of world resource usage.

What do you mean? People buy hardware and use energy just to get money (for otherwise meaningless activity) ... until reaching profitability level, like burning $99 worth resources to get $100 banknote. In contrast, mining other resources like gold is not otherwise meaningless ( https://www.mecmining.com.au/top-5-uses-of-gold-one-of-the-worlds-most-coveted-metals/ ). But most importantly it is limited - in contrast to unlimited number of cryptocurrencies they can create, it is impossible to maintain exponential growth of gold mining ... while cryptocurrencies can use literally all available resources, growing exponentially until saturating on 100% of world energy production cap.

Exactly - pathological mechanisms can develop when society no longer needs to focus on survival - perfect connection, thanks! Thousands, hundreds of years ago most of society had to focus on crucial activities like food production. With efficiency growth, now nearly nobody cares about food producers minorities, leaving place for growth of various activities with questionable effects for well being, survival of our civilization. Crypto is the next level - literally giving a person $100 banknote for burning $99 worth of resources - leading to exponentially growing movement of resource burning ... like if Calhoune mouses start burning provided food. How long can a civilization survive when reaching such higher level Calhoune-type mechanism?