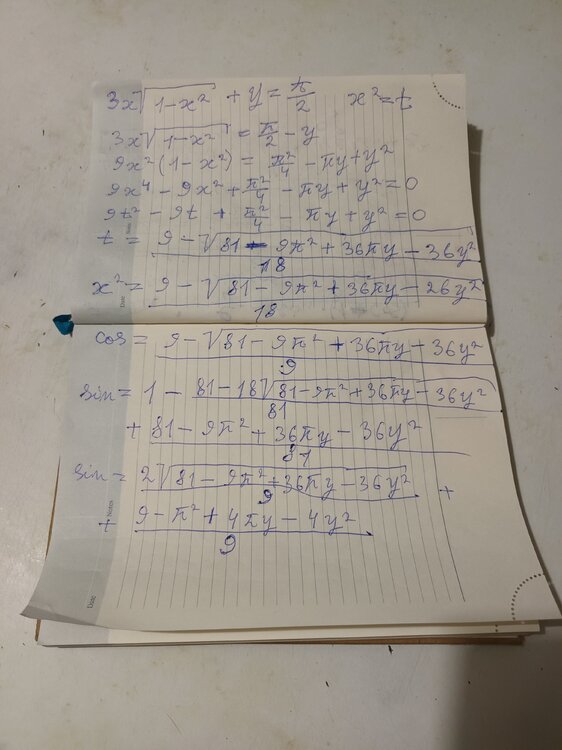DimaMazin

a=2sin(a) I have no higher education and I am janitor therefore I don't understand why we can not to exactly solve it relative to Pi. Can next method be correct?

Seems we can exactly solve such problem: a - sin(a) = (Pi - 2)/2 😛

I correctly started, but in frame S' we should consider instantaneous acceleration of carriages from frame S to frame S". S is traveling at v in frame S'. S" is traveling at u' in frame S'. When ve have correct formula then we can try to serch for neutral simultaneity.

y = cos(a)/(1+2sin(a)) cos(a)/(1+2sin(a))=(p-6a)/2

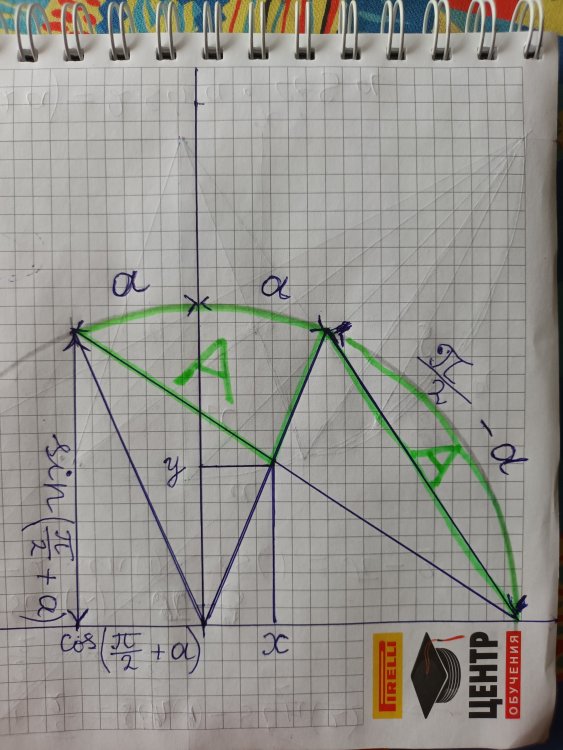
Maybe you think sin and cos are sin(a) and cos(a)? No. sin is sin(p/2 +a) and cos is cos(p/2 +a) as it showed on diagram.

Can such problem be solved? Area A =area of the green segment. x=-cos/(1-2cos) y=sin/(1-2cos) sin/(1-2cos)=(p-6a)/2

Russian military don't want to be under hood of KGB. Do you think after the arrest the Russian bloggers cannot publish independent information?

Russian troops use Telegram for transmit information.

Thanks. My idea is wrong again.

How to check next idea: t=2sin(t) a= cos(a) b=2(t-a)+a sin(b)=a - sin(a) ?

Lets consider known equation: dsin(a)=cos(a)×da da is near zero I speculatively derivated from it this n÷(cos(a1)+cos(a2)+...+cos(an-1)+cos(a))=2sin(a)÷(a+sin(a)×cos(a)) n is infinite natural number a1=a÷n When n is small then the equation is approximate. Can it be so?

Can sin(1 rad) be 75000×Pi ÷ 280009 ?

Thanks. My idea is wrong.

Let's consider speculation how to solve a=2sin(a). Sector of such angle is special. Any sector has two parts of its area. One part of its area=sin/2. And second part is segment area. Two parts of the sector are equal. Then let's consider else two sectors. Sector of half of the angle a/2 and sector of angle (Pi-a)/2+a. My speculative idea is: (area of segment of angle(Pi-a)/2+a) ÷ sin(of the angle)/2 = sin(a/2) ÷ (area of segment of angle a/2) Can it be so?

Let's consider hypotheses. When velocity U is bigger than c, then we use velocity of MD65536 V=v/(1-1/gamma)) U=u/(1-1/gamma)) Then u=2Uc2/(U2+c2) Then we should define u' u'=(v+u) / (1+vu/c2) Then we can define U' using again formula of MD65536 U'=u'/(1-1/gamma) U'=u'/(1-(1-u'2/c2)1/2)😛