phyti
Senior Members-
Posts
212 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by phyti
-

Concerning Infinity (of course)
phyti replied to Boltzmannbrain's topic in Linear Algebra and Group Theory
Boltzmannbrain; s=Σ (1/2n), for n=1 to ∞ s is a series of partial sums, a variable and a geometric progression for this example. The sum s will converge toward a limit. The limit of s is a constant c=1, also denoted as an asymptote. s approaches c, but by definition of 'infinite' (without limit/last term), never equals s. s=(1/2+1/4+1/8+...+1/2n) for n terms. 2s-1=(1/2+1/4+1/8+...+1/2n-1)=s-1/2n for n terms. s=1-1/2n 1/2n>0 for all n. For large values of n, 1/2n is judged insignificant for the purpose and the limit is used to represent the value of s. This would also apply to the series .999R converging to its limit 1. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; finally applied it, without justification, to the mathematics of infinite sets. This is the Fall and original sin of [Cantor's] set theory …." (Weyl, 1946) _________________ "You fail to recognise that there are sequences in the set of sequences that are not in the list of sequences. By failing to recognise this, you are unable to understand Cantor's proof because this is precisely what Cantor is proving." Do you think repeating this multiple times will make it true? Cantor fails to prove his idea via the diagonal argument with badly executed manipulation of the list. You don't like the conclusion which is; humans can't comprehend 'infinity'. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; KJW; -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
Look again at the binary tree. There are no diagonal sequences. All are horizontal, as originally shown by Cantor. The diagonal is his misdirection. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; Cantor's illusion.pdf KJW; Something went wrong! Cantor's illusion.pdf -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; [/quote] Where did you get the idea that the sequences are random? The more correct term is "arbitrary", which is not the same as "random". In fact, Cantor attempts to construct an infinite list of all possible infinite sequences. But regardless of how that is attempted (represented by a list of arbitrary sequences), the list will always be missing the sequence constructed from the negation of the diagonal.[/quote] 'Arbitrary' and 'random' are synonyms for each other. 1. Before he defines b, all s(equences) are horizontal, there are no diagonal s. 2. He defines D from the list as all the elements with coordinates (u, u). 3. If he forms the negation of D as E0 and states it's missing from the list, he contradicts himself, since he has assumed D is a member of the list. The building set is binary {m, w}, they occur in pairs! If D then E0. -

Proportion of the area covered by circles
phyti replied to Dhamnekar Win,odd's topic in Applied Mathematics
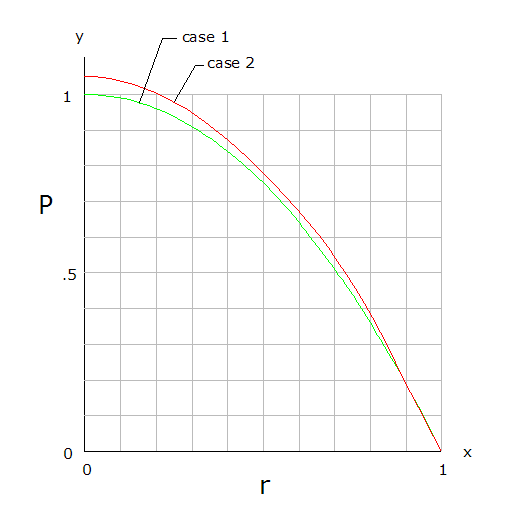
As Rn approaches R, rn approaches 0. When Rn equals R, rn equals 0. Why doesn't P=outer band/area of circle=0? -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; The flaw is his definition of a diagonal sequence/string/s. It depends on all s listed, and differs from those. He defines the initial list as consisting of horizontal s. That's why the random properties of the s and the list which is itself a random s are included. If the s are parallel there can't be any influence of one on any other. I.e. they are independent. False. I use the infinite set N. I haven't seen an answer to 'what is the magic n when the split occurs' that he describes in excerpt 2 below. Those are the only ones we can form. No one has or can produce an infinite list. It's not an abstraction but a fantasy. No one will ever see a list for the set N. excerpts from 'Cantor on Set Theory': 1. "This correlation, if it is possible at all, is, as one easily sees, always completely determinate; and since in the widened number sequence there is always one and only one number alpha such that the numbers preceding it (from 1 on) on the natural succession have the same Anzahl, one must set the "Anzahl" of both these "well-ordered" sets directly to alpha, if alpha is an infinitely large number, and to the number alpha-1 which immediately precedes alpha, if alpha is a finite integer." 2. "When I conceive the infinite … there follows for me a genuine pleasure … in seeing how the concept of integer [der ganze Zahlbegriff], which in the finite has only the background of number [Anzahl], as it were splits into *two* concepts when we ascend to the infinite" He rambles on about determinate order/well ordered. How can there be an ordered set/list for an infinite set? Using {0, 1} in that succession: 1. (000000...), 2. (000000... where/when do we put the first 1? If you have two identical s that only differ in the last symbol, you can't sort them, since there is no last symbol. Thus most if not all mathematical operations that are defined for finite (things with boundaries) can't be applied to things without boundaries, including measurement (counting). But that is what Cantor is trying to do. The meaningless phrase in red is more of the nonsense cited by Wittgenstein. -
What is time? The operational definition of assigning a time to an event as mentioned by A. Einstein in his 1905 paper is essentially what it is, and how it's been done since humans appeared. It is a correspondence convention, i.e., assigning events of interest to standard clock events, a measure and ordering of activity, with 'time' always increasing/accumulating. It is an accounting scheme developed out of practical necessity, for human activities like agriculture, business, travel, science, etc. The unit of measure for time initially referred to relative positions of astronomical objects, stars, sun, and moon, which implies earth rotations and earth orbits. All units of time are by definition, involving spatial motion or distance. The clock further divides the day into smaller units of measure. Current scientific research requires clocks that generate smaller and more precise periods than those of the past. The second is defined as n wave lengths of a specific frequency of light, a distance, but labeled as "time". If we use a light based clock to time the speed of an object along a known distance x, what are we actually doing? We are comparing the simultaneous motion of an object to the motion of light for a duration (number of cycles). The result is a ratio x/s = vt/ct = v/c or speed. It should be obvious that the number of cycles serves to correlate the positions of the object with the positions of the light signal, for simultaneous comparisons. If you use Minkowski spacetime diagrams the vertical scale is not 'time', but ct, light path distance, i.e. they plot speed. This allows a simple comparison of equivalent entities, without consideration of the nature of those entities. The scaling of the time variable by c allows an analysis of extremely short durations of time. quotes by the author of SR From 'The Meaning of Relativity', Albert Einstein, 1956: page 1. "The experiences of an individual appear to us arranged in a series of events; in this series the single events which we remember appear to be ordered according to the criteria of "earlier" and "later", which cannot be analyzed further. There exists, therefore, for the individual, an I-time, or subjective time." page 31. "The non-divisibility of the four-dimensional continuum of events does not at all, however, involve the equivalence of the space coordinates with the time coordinate." page 32. "Finally, with Minkowski, we introduce in place of the real time co-ordinate l=ct, the imaginary time co-ordinate..." [This does not mean 'time' is literally imaginary. The 'i' in the complex plain indicates a coordinate independent of the others, when (x, y, z) are present.] time and perception Subjective time requires memory, which allows a comparison of a current state to a previous state for any changes, which lends itself to an interpretation of time flowing. Patients with brain damage to specific areas involved in maintaining a personal chronology, lose their ability to estimate elapsed time, short or long term. Consider the fact that people waking from a comatose state, have no memory of how much elapsed time, whether hrs, days, or even years. Consider one of the greatest misnomers ever used, 'motion pictures' or 'movies', where a person observes a sequence of still photos and the mind melds them to produce moving objects where there is no motion. These cases show time as part of perception. Special Relativity then predicts alteration of measurement and perception via motion. misc. It was Minkowski who advocated the mathematical manipulation of the expression for the invariant interval from an equality to a generalized form of four variables, producing spacetime. I refer to the Minkowski version of SR as a 'lines on paper' theory. Time is represented as a line, removing any attributes that would distinguish its identity from other variables, a line is a line. Math equations that express a behavior as a function of time, are misleading when the time is interpreted as a causative factor. The time of an event must be assigned after the event occurs, i.e. after awareness! If a nova is observed in 2010, and is 100 ly distant, it didn't happen because it was 1910 on earth. It was the physical processes already in place that reacted to an unstable state. A person dies, not because it's his 'time', but because his biological system reaches a state that can't be maintained. Which brings us to the real issue (for me) perpetuating the millenia of debating 'time'. No one wants to be informed "atomic clock at NIST has a hole in it and time is running out". Time implies longevity. People gain some sense of security if they think there is an invisible entity behind the scenes arranging and scheduling more events. Time is not an issue for physics but for psychology. Source: 15 years participating in forum debates, and Scientific American, 'A Matter of Time', vol. 287, 2002.
-

Proportion of the area covered by circles
phyti replied to Dhamnekar Win,odd's topic in Applied Mathematics
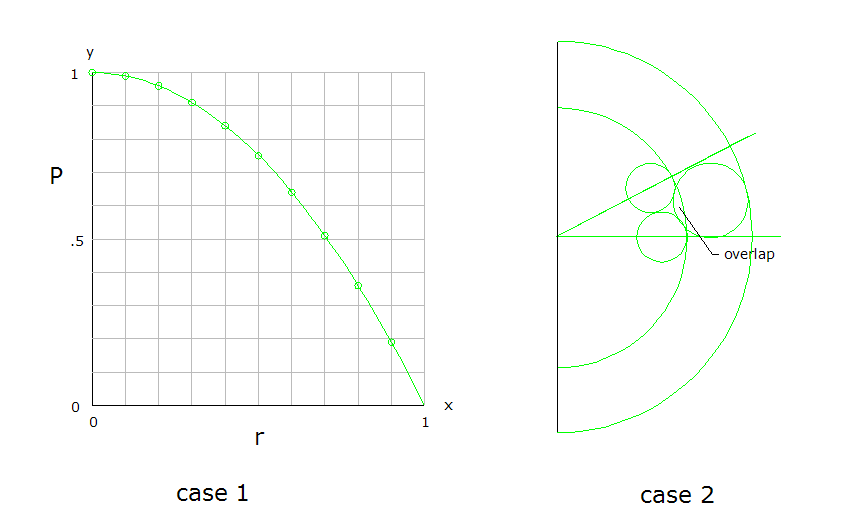
Dehamnekar: Was uncertain about case-2, didn't make any calculations. Because of overlap, (A+B)>1 initially. "When A=B, there are small portions of the band remaining." This needs clarification. As A expands toward B, the band shrinks to 0 at A=B. My response is based on the case-2 picture. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
Per the constructivist view, no one can nor have formed an infinite list. No one can even form an infinite sequence! The 'infinite list' is a contradiction of terms. If it has no last element, it would always exist in an incomplete state. You ignore the fact that the rule of formation determines the geometric form of the list, not the word 'infinite'. If Cantor' diagonal argument is false, his followers would miss their 'feel good moments', believing they can comprehend deep things. He would have had better credibility by descending from a high place with a stone tablet with aleph0 etched on it. -

Proportion of the area covered by circles
phyti replied to Dhamnekar Win,odd's topic in Applied Mathematics
Dehamnekar: Let B=outer circle area πR2 and A= inner circle area πr2 . P=ratio of outer band to B, = (B-A)/B. Case 1. P=1-A/B=(1- r2/R2) . The graph plots P as r varies. Case 2. The inner circle overlaps the outer band. When A=B, there are small portions of the band remaining. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
Another frustration of the internet system! They offer 'file sharing' which should work without being a subscriber! Here is the pdf (many viewers don't have MS os). Cantor's illusion.pdf -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
In case there is anyone else interested in the subject of Cantor's diagonal argument, the latest paper is here: https://drive.google.com/file/d/17Zz39YzAEEvD5pWB0f4NihEucQfZ3RHU/view?usp=sharing -

Proportion of the area covered by circles
phyti replied to Dhamnekar Win,odd's topic in Applied Mathematics
Dehamnekar: The author made the problem more complicated than necessary. No need to count the circles in the outer band. Let B=area of outer circle and A= area of inner circle. The ratio P =(B-A)/B. The limit of A=B, thus P=0/B. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; You still don't understand, my argument with Cantor's argument doesn't involve properties of numbers. As he states in the 1891 paper "However, there is a proof of this proposition that is much simpler, and which does not depend on considering the irrational numbers." It involves two alphabetical symbols used in forming sequences/patterns as members of a set M. The elements are sequences, NOT numbers. The integers in the set N are used for the purpose of forming an array within a coordinate system (v, u). L His goal is to convince the reader that the list will be incomplete. Thus the cardinality (number of elements in a set) L is greater than N. This allows him to sell his transfinite numbers. I will leave you with your math diversions. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
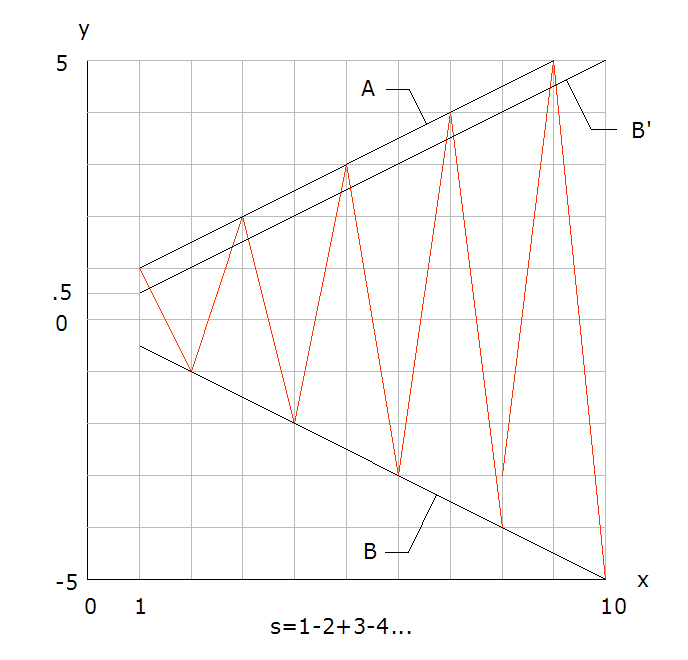
KJW; fig.1 shows the alternating series s=(1-2+3-4+5-6+7-8...) as a discontinuous function. fig.2 shows continuous functions A and B. For A y=x. For B y=-x. If A and B are applied to fig.1, the difference A-B=0 for all x. The B function has been shifted by -1 in fig.2. The equation for B is transformed from y=-x to y=-x-1. Now the difference A-B=x-(x+1)=(-1) for all x. The shift results in subtracting the B value for x from the A value for x-1. -

problem with cantor diagonal argument
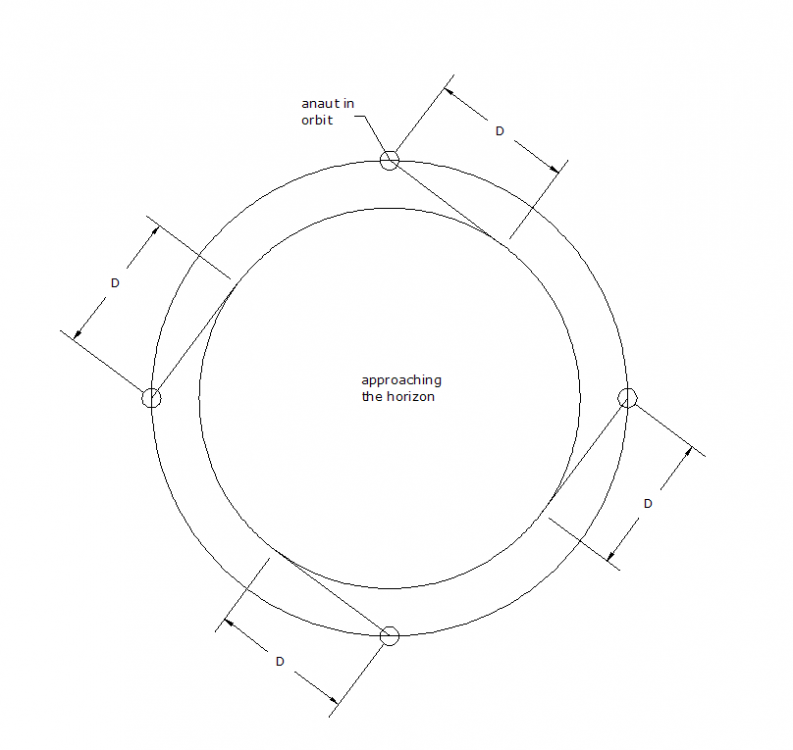
phyti replied to phyti's topic in Linear Algebra and Group Theory
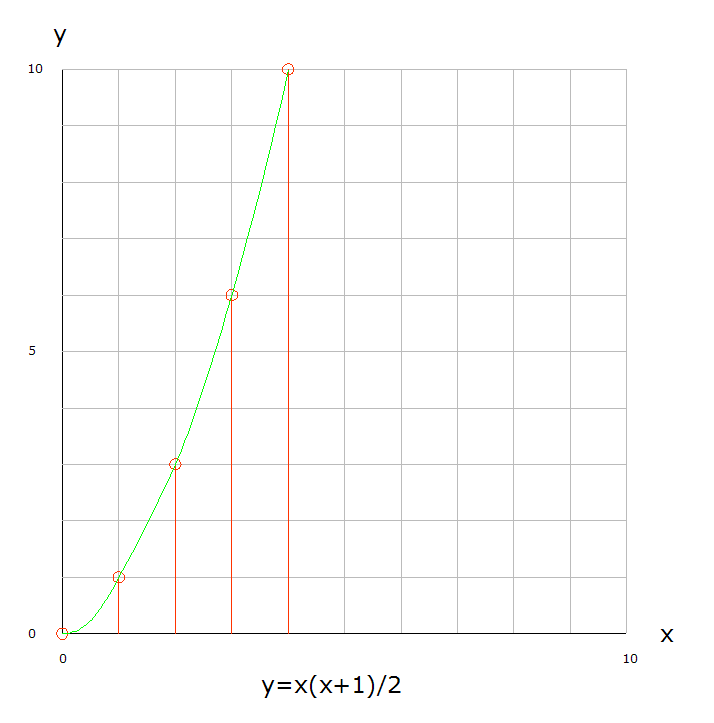
You answered your question in the last line! The anaut can't get any closer to the horizon. The horse keeps moving forward to reach the carrot on a stick but never reaches it. Infinity can appear in cases other than math. KJW; Ref. '1+2+3+4+', Wiki. The partial sums are discrete integers. There are no bands of areas forming a step function as shown in the Wiki article. The green curve appears to be enclosing an equivalent area of the bands. No reason for y to be <0 when x=0. Ref. png graphic: Using y=x(x+1)/2 the green curve contains the partial sums for all n. The y increment remains increasing without limit, thus no last term. alternating series s=(1-1+1-1+1...) 1. For self referential, s-1= -s, thus s=1/2 avg . 2. If summed sequentially, s=0 or 1, with an avg. of 1/2. 3. If sorted and summed, s=(n-n) = 0, or s=[(1-1)+ (1-1)+ (1-1)+ (1-1)...] = 0. Depends on the method of manipulation. alternating series s=(1-2+3-4+5-6+7-8...) s=(1+3+5+7...)-(2+4+6+8...)=A-B s=Σ(2x-1)-2Σ(x), x varies 1 to n. s= 2Σ(x)-n-2Σ(x)=-n. Ref. png graphic The measurements are alternating which skews the differences. Using the envelope measurements which are linear, and B' is the mirror image of B, the difference is .5. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
-

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW; Didn't say you did. I'm referring to Cantor's ideas. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
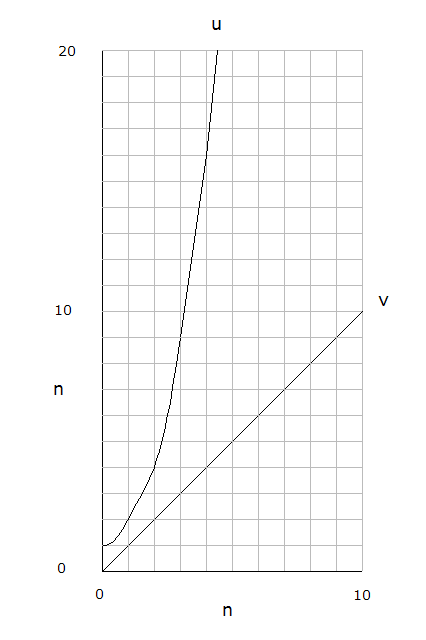
KJW; [quote Earlier in this thread, you indicated that there is only one infinity. Have you changed your mind on that? [/quote] No. 'Infinite' has no superlative state. Comparison of 2 quantities results in equal or not equal. If not equal, one is greater than the other. For a sample size >2, if one is greater than all others in a sample s, then it is the greatest relative to s. Cantor quote: "When I conceive the infinite … there follows for me a genuine pleasure … in seeing how the concept of integer [der ganze Zahlbegriff], which in the finite has only the background of number [Anzahl], as it were splits into *two* concepts when we ascend to the infinite – one one of number [Anzahl] which is necessarily bound to a lawlike ordering of the set [Menge] by virtue of which it becomes well-ordered (wohlgeordneten)." So again I ask, what is the magic n in N which is infinite by definition, where the set becomes aleph0? Cantor's error is assuming the diagonal D extends to the end of the list forming a geometric square, excluding its negation E0. That's not possible using established math procedures plotting the relation between u and v. The variable v is a linear function, the variable u is an exponential function. They are never equal as shown in the graph. The (u, v) relation depends on the number of symbols used in the formation of sequences. -------------------------------------------------------- I can't imagine 'approaching infinity', yet it's a common phrase in most text books. Do you know how? [ref] 'Cantor on Set Theory',Source: Ewald, W., From Kant to Hilbert, Oxford 1996. -

problem with cantor diagonal argument
phyti replied to phyti's topic in Linear Algebra and Group Theory
KJW;