phyti

Jeff; He has already defined M. It isn't necessary to keep defining it for every detail he describes. Everything stated after that is within the same context of an infinite set/manifold M. The beginning of an infinite random list, with one infinite sequence per line, and line 1 blank. A random sequence can be placed anywhere in the list except at the end, since an infinite list has no end, but we have access to its beginning s1 s2 010010... s3 101011... s4 111000... s5 000111... s6 011011... s7 111111... sx 110000... Using Cantor's diag. method, sx is not in the list. Put sx in line 1, now it is.

wtf;

Why does he say . "Let M be the totality [Gesamtheit] of all elements E."

Jeff;

Follow these links. https://www.logicmuseum.com/index.htm Subjects in logic and metaphysics Cantor's Philosophical Writing On an Elementary Question of Set Theory (Georg Cantor) https://www.logicmuseum.com/authors/index.htm Primary sources in logic and metaphysics (Logic Museum II)

Jeff; Keeping it simple, using 0 and 1 for symbols and S for sequence or string, divide M into 2 subsets, M0 containing S beginning with '0', and M1 containing S beginning with '1'. S=0000... is a member of M0, true or false? S=1111... is a member of M1, true or false? "if alpha is an infinitely large number," From CANTOR'S PHILOSOPHICAL WRITING CDA Both from THE LOGIC MUSEUM Copyright © E.D.Buckner 2005

studiot; Isn't that is about power sets? This is about the method of using the diagonal in a random list, not about numbers in any form. He used alphabetical symbols in his cda, not numbers! Jeff; It's possible you have a problem in comprehension. Read the beginning of his argument. 1. Cantor defines his set M as the totality of all elements E, where each E contains an infinite (unlimited) number of characters (symbols), selected from a binary set of two, {m, w}. He "maintains" (declares) the set M "does not have the power" (cardinality) of N the set of integers. 2. Cantor is not using subsets or functions. He defined all the elements needed. Cantor is comparing two sets M and N, by attempting a 1 to 1 correspondence. If that fails, then he can sell his transfinite numbers. He begins with the standard 2-dimensional array for three E sequences/strings. He defines a diagonal D, and in the process forms a duplicate sequence and alters the random array with an ordering rule. In a random list, there is no order. Each row can appear anywhere within the list, thus its name! Why didn't his negation E0 inherit the same 45º angle from diagonal D? Then they could coexist as shown in fig.2 of the pdf. Here is a phrase from his philosophy on set theory "if alpha is an infinitely large number," What is the meaning of the red if any? Another of my favorite quotes. Wittgenstein: "Where the nonsense starts is with our habit of thinking of a large number as closer to infinity than a small one".

Boltz; Anyone can copy Cantor’s method and get the same result of the ‘missing’ sequence which is misdirection similar to what the illusionist does. He defined two different types of sequences, horizontal and diagonal, mixed them in the same list and fooled himself into thinking he proved his need for transfinite numbers. S1 010101 S2 _1 S3__1 S4___1 S5 ____1 … _ is either 0 or 1 In the above list, which sequence, horiz or diag, gets the id of S1?

Jeff; His proof using the diagonal is flawed for the reasons mentioned. If a sequence D is a member of M or any binary set of symbols, then its negation must also be a member of M. You are in denial.

Jeff; Cantor wanted to prove an infinite list/enumeration of sequences contained in his set M was greater than the infinite set N of natural numbers, thus no 1 to 1 correspondence and requiring his transfinite numbers. Showing incomplete partial lists would not accomplish his goal. His two quotes indicate his goal. GC:"Let M be the totality [Gesamtheit] of all elements E." M is the set of all E sequences. GC:"I maintain now that such a manifold [Mannigfaltigkeit] M does not have the power of the series 1, 2, 3, …, v, …." M is greater in number of elements than the set N of natural numbers. You: "Neither "v" nor "u" are in the set M, they are natural numbers not binary sequences (rows)" No one said that, so stop reading things into the post that aren't there. Cantor uses a u,v coordinate system to locate any symbol in a 2 dimensional form of a list. Example 1. An excerpt from Cantor's philosophical writing: 1. As for the mathematical infini 2. te, to the extent that it has 3. found a justified application 4. in science and contributed to 5. is usefulness, it seems to me 6. that it has hitherto appeared 7. principally in the role of a 8. variable quantity, which eith 9. er grows beyond all bounds or 10.diminishes to any desired minu 11.teness, but always remains fin 12.ite. I call this the improper The red diagonal D = Aeusu_ie_stl, where _ is a space. The example contains 12 statements formed using rules of grammer. Its purpose is to show D is not a statement just because it originates from a list of statements, only a random sequence of symbols, formed by a simple rule of selection. Each symbol in D has the coordinates (u, u). The rules of formation or definition are different for the list and the diagonal. In Cantor's argument the initial list contains randomly entered E sequences composed of two symbols. Each E sequence is 1-dimensional and extends without limit horizontally with a varying coordinate v, (1, 2, 3, ...) The diagonal D has the coordinates (u,u), using the same rule of selection. D is not an E just because it originates from a list of E's. The rules of formation or definition are different for the E list and the diagonal D. The D sequence is also 1-dimensional but extends horizontally and vertically, requiring two coordinates (u, v) for each position. The difference between D and E requires an analysis of the small details which apparently were never done. Another case of evidence in plain sight, the most difficult to detect. Accepting D and E as equivalent, a problem appears where they intersect as in the pdf fig.3. An E and a D can occupy the same position, only if the symbol is the same for both. For the negation of D, E0 obviously cannot appear anywhere in the list. Not because of any oversight, but exclusion resulting from D, and that only because D is the first in the list. There are other exclusions. If E has 1 symbol in column v that differs from D, it is excluded from that row. If E has 2 symbols in columns v1 and v2 that differ from D, it is excluded from those 2 rows. In general if E has k columns with symbols differing from D, E is excluded from those rows. His diagonal imposes an order on a random list, which has no order. I include the above to show how he convinced himself and others while neglecting the properties of a random list. Using the term 'contrived diagonal' is not implying he intended to deceive anyone. What would prevent a random sequence from being inserted anywhere in a random list? As shown in the pdf, if the diagonal began at row 2, then E0 could appear at row 1. You are confused because you didn't see what you wanted to see. Read his biography and philosophical thoughts, and his correspondence with his contemporaries. Many disagreed with him. One of my favorites: Leopold Kronecker: "I don't know what predominates in Cantor's theory - philosophy or theology, but I am sure that there is no mathematics there."

Jeff; After a few failed attempts, Cantor's error is exposed. Keep in mind the nature/properties of a random list, a 1-dimensional sequence, and a 2-dimensional sequence. Read the pdf without any preconceived notions. Cantor diagonal argument resolution.pdf

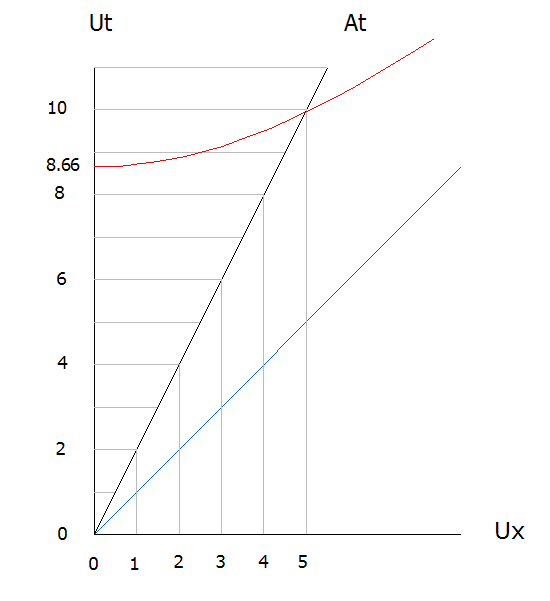
; Minkowski inflated the time scale for a space-time plot from t to ct, enabling an analysis of extremely short durations of time, and allowed comparisons of object motion to light motion (apples to apples), or vt/ct, which equals v/c or speed. With two possible directions ±(x, y, z), a history of each position with a corresponding time, becomes a velocity profile. It is not interpreted as a geographical map. In the standard example, Ut is the time scale for the reference frame and Ux is the x coordinate for A moving at .5c relative to U. An object moving at c is represented by the blue line with a slope of 45º, which can only be light. The red calibration curve (as labeled by Max Born) represents a constant time wherever it intersects a velocity profile. The spatial units will match the time units. Thus x=5 light sec. when Ut=10 light sec, and At=8.66 light sec. When Einstein developed Special Relativity, he defined the sum of squares of the velocity components (x, y, z) as an invariant interval S, and the corresponding time for that interval as S/c. Minkowski did what mathematicians do, simplify and generalize by redefining Einstein's time variable using complex notation as -ict, I.e. it is only a mathematical 4th dimension. The 'time' identity was removed when it became must another line. Moving in time is a metaphorical expression popularized by scientists such as Brian Green in books and on PBS. Referring to the plot, if A remains at Ux=0, there is no motion, but his clock keeps ticking. If the velocity components =0, t=0/c=0. If the clock moved at c, it would cease to function as a clock

Using a finite set of 10 unique sequences, there are 10 possible S for position 1, 9 possible S for position 2, 8 possible S for position 3, ... 1 possible S for position 10. A total of 10! random lists, to show there is not just 1 random list L for the sequences in Cantor's set M. Each L begins with a different sequence, thus a different diagonal D. One of those L's will contain a diagonal E0 that Cantor declared missing from the L containing the original D. Cantor makes his own contradiction by ignoring the complementary nature of a sequence and its negation, i.e. they come in pairs for a binary set of 2 symbols.

"If E1, E2, …, Ev, … is any simply infinite [einfach unendliche] series of elements of the manifold M, then there always exists an element E0 of M, which cannot be connected with any element Ev." E0 is the negation of D, the diagonal used to form E0. The negation of a sequence has all positions with m and w interchanged. That is the connection.

; "If E1, E2, …, Ev, … is any simply infinite [einfach unendliche] series of elements of the manifold M, then there always exists an element E0 of M, which cannot be connected with any element Ev." "From this proposition it follows immediately that the totality of all elements of M cannot be put into the sequence [Reihenform]: E1, E2, …, Ev, … otherwise we would have the contradiction, that a thing [Ding] E0 would be both an element of M, but also not an element of M." Cantor believes there is a hierarchy of infinities, a communication from above which he is obligated to explain to the world. Cantor is selling his idea of transfinite numbers to anyone who will listen. In the above quotes he states there are always elements of M which differ from those in any list, thus there cannot be a one to one correspondence with the set of natural numbers N, even though N is inexhaustible. The Ann and Bob example contradicts his idea, since one will have an infinite list containing the sequence E0 that the other infinite list does not contain.

That's what I said. "I.e. a missing sequence is only relative to an individual list". Here is what Cantor said. "If E1, E2, …, Ev, … is any simply infinite [einfach unendliche] series of elements of the manifold M, then there always exists an element E0­ of M, which cannot be connected with any element Ev." "From this proposition it follows immediately that the totality of all elements of M cannot be put into the sequence [Reihenform]: E1, E2, …, Ev, … otherwise we would have the contradiction, that a thing [Ding] E0 would be both an element of M, but also not an element of M." From the example T1 which is missing from Ann's list is included as D2 in Bill' list. Thus it is not missing from M. Missing from a subset does not imply missing from the complete set.

Ann and Bill independently work on examples of Cantor's diagonal argument. Ann: 111001... 000111... 101100... 110011... 000110... 010110... transforms diagonal D1 to alternating '01' sequence T1, 010101... which can't appear in any list per the cda. Bill: 000110... 010110... 110001... 000111... 101100... 110011... transforms diagonal D2 to alternating '10' sequence T2, 101010... which can't appear in any list per the cda. If D1 and D2 appear in any list, they must be members of the complete list. T1=D2. I.e. a missing sequence is only relative to an individual list.